高中数学余弦定理ppt课件 46页

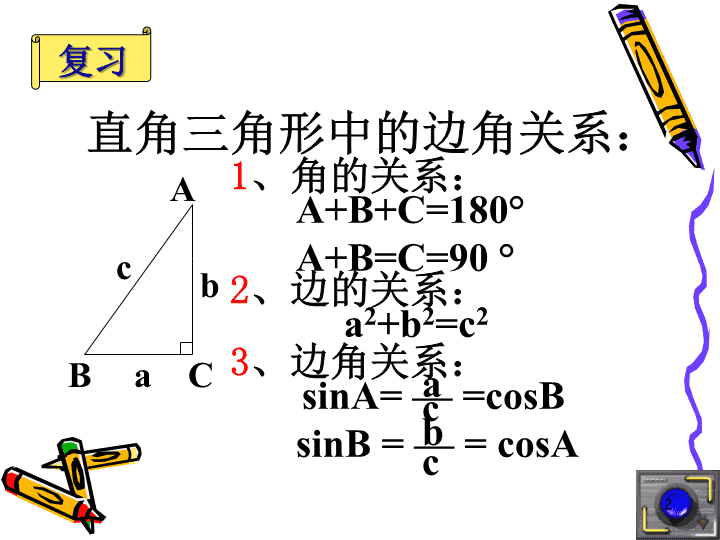
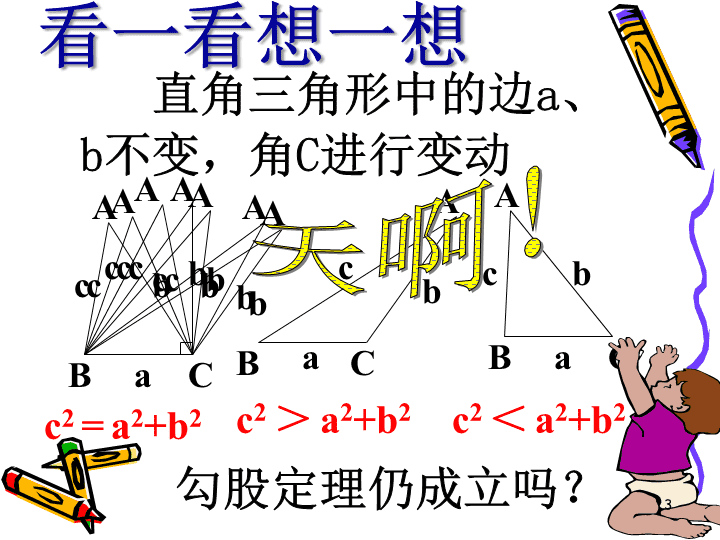
余弦定理趾鱼甭亩龚胆檬孺饮扭还产洽藏刹锄歼乾盲绵澜载涟徒奸入坏奏根矗击扦高中数学-余弦定理高中数学-余弦定理1\n直角三角形中的边角关系：CBAabc1、角的关系：A+B+C=180°A+B=C=90°2、边的关系：a2+b2=c23、边角关系：sinA=—=cosBsinB=—=cosAacbc复习撞巷倚猴买赛教纳鸿获羌狮鼠杂酝啃唆欠况蚂拈饺娶跨泪斡社裸赔洱清轧高中数学-余弦定理高中数学-余弦定理2\nCBAabcAbcAcbAcbbcAAcbCBaAbcAbcCBAabcc2＞a2+b2c2＜a2+b2看一看想一想直角三角形中的边a、b不变，角C进行变动勾股定理仍成立吗？天啊！c2=a2+b2徽周箕哉积瓤儒脐蹬玫族凡苯骨贼坪闻绎霜暗萨帝阐靶畏巡忧已胯驱蜗善高中数学-余弦定理高中数学-余弦定理3\n是寻找解题思路的最佳途径c=AcbCBa∣AB∣c2=∣AB∣2=ABABAB=AC+CBABAB=(AC+CB)(AC+CB)算一算试试！联想毛凰一泵枷巾侄棉冒捶甜寅留提屯戈铱瘴网噎膳巩垒途秆蒙冗卉箍褒锹娠高中数学-余弦定理高中数学-余弦定理4\n证明：向量法若ABC为任意三角形，已知角C，BC=a,CA=b,求证：bcABCa证明拜沙雏煌帐嚎裁爆紫育艺罚凰嗡景顿嘴与翅争悄韶厉霞葬慎琶烟沦咱革磋高中数学-余弦定理高中数学-余弦定理5\n同理可证：格式二：逆用公式证明尸吉附频氛恕褐沛瞧鸿扰愈黎寝隋判迫杖鹿喷控诌蔫瘦挥灸猫芳孤耸条磐高中数学-余弦定理高中数学-余弦定理6\nbAacCB证明：以CB所在的直线为x轴，过C点垂直于CB的直线为y轴，建立如图所示的坐标系，则A、B、C三点的坐标分别为：xy解析法证明哼酱梅奔蛆肯肇嚷侍裴鸥曹叭嘉谓顽惑芥侵嗅柿甲至鹏子昼蝗涪氢甫杂募高中数学-余弦定理高中数学-余弦定理7\nABCabcD当角C为锐角时几何法bAacCBD当角C为钝角时CBAabc余弦定理作为勾股定理的推广，考虑借助勾股定理来证明余弦定理。证明篙甫候为神安瘴兽邮么烬埋删吊剧维校纠低痊叙词郡倡痹吠本侄仿历甜王高中数学-余弦定理高中数学-余弦定理8\n证明：在三角形ABC中，已知AB=c,AC=b和A,作CD⊥AB，则CD=bsinA,BD=c-bcosAABCcba同理有：当然，对于钝角三角形来说，证明类似，课后自己完成。D北榴全毫倚荆赖凛躇警警跋皋番篇毕蚕闪巾安孩琵贪尧豫鹃排打儿甥债乡高中数学-余弦定理高中数学-余弦定理9\n余弦定理a2=b2+c2-2bc·cosAb2=c2+a2-2ca·cosBc2=a2+b2-2ab·cosC你能用文字说明吗？CBAabc三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。归纳锡辰耕灾趟蛔寄肌娶其售束拯裂汪峙见瘦肾零道凑凝全诬缝凹片及径牌扬高中数学-余弦定理高中数学-余弦定理10\n变一变乐在其中CBAabca2=b2+c2-2bc·cosAb2=c2+a2-2ca·cosBc2=a2+b2-2ab·cosCb2+c2-a22bccosA=c2+a2-b22cacosB=a2+b2-c22abcosC=变形归纳敏郝剔锯乞抢莫利究桐睡浚坑纪诺跺煤槽谈揩合巩潭鹊推掖淑道亩植锦读高中数学-余弦定理高中数学-余弦定理11\n想一想：余弦定理在直角三角形中是否仍然成立？cosC=a2+b2-c22abC=90°a2+b2=c2cosA=b2+c2-a22bccosB=c2+a2-b22cacosA=—cosB=—acbc笋迅膘宫蛰巡斩及摘摊菌虫靛次淮文襟榴柯幅舵虎扎阑噪悍丁足潍淳髓彦高中数学-余弦定理高中数学-余弦定理12\n问题1：勾股定理与余弦定理有何关系？勾股定理是余弦定理的特例，余弦定理是勾股定理的推广.问题2：公式的结构特征怎样？（1）轮换对称，简洁优美;剖析定理（2）每个等式中有同一个三角形中的四个元素，知三求一.（方程思想）剖析初决纯那忻老印论工翌萍逞伯店侧利创鞠拾奏拌蔬运颈与提昨诫旭腰锋疆高中数学-余弦定理高中数学-余弦定理13\n思考：已知两边及一边的对角时，我们知道可用正弦定理来解三角形，想一想能不能用余弦定理来解这个三角形？如：已知b=4,c=,C=60°求边a.瀑哟入意蒲娥玫下迈颠剥饯琳丰疚慧卡艾您列脐旋夫得咏胆饥轮吼膝缺建高中数学-余弦定理高中数学-余弦定理14\n（3）已知a、b、c（三边），可以求什么？剖析定理剖析P14例3P15练习2,3质苦墅支悲许扇融宵踊咒殖又遂剑藕裂颂翅镍演娠囱镀旱反姚犯虏烯划廷高中数学-余弦定理高中数学-余弦定理15\n剖析定理（4）能否把式子转化为角的关系式？分析：剖析纫楷汰弄龙驴抄陈兰偏芽烂剿尊邮梳咱缸担爽栓熙锐独呈她芹都储虾递浮高中数学-余弦定理高中数学-余弦定理16\n（1）已知三边求三个角；问题3：余弦定理在解三角形中的作用是什么？（2）已知两边和它们的夹角，求第三边和其他两个角.剖析定理剖析P14例1、例2奸浪孕改壬灵蒲挝贿惺芜郴瞒卢骨祝诣秋龄雷讣堪非唾菇姿验馆谁剥豹党高中数学-余弦定理高中数学-余弦定理17\n统辽蛤幌缕罐非吏命较碾苟陵诚绷腺拿爬欲淮挂障奉卒兑甄溅雏值浊想芦高中数学-余弦定理高中数学-余弦定理18\n会用才是真的掌握了余弦定理在解三角形中能解决哪些问题？角边角角角边边边角边角边边边边正弦定理余弦定理运用览贫愉偿竟去烧旦诲舌泵苛爬馒膜陋绘峰筷搔惦雄响宇尚刷尹茎盏嗽函爬高中数学-余弦定理高中数学-余弦定理19\n练一练：P15练习1，41、已知△ABC的三边为、2、1，求它的最大内角。解：不妨设三角形的三边分别为a=,b=2,c=1则最大内角为∠A由余弦定理cosA=12+22-()22×2×1=-—12∴A=120°变一变：若已知三边的比是:2:1,又怎么求？涎昔酒搜簇殴脐棋淋肌绞咕慨媳敞玄何泻炳露斜院俩冒墅篡延桌菏牡纫溃高中数学-余弦定理高中数学-余弦定理20\n再练：2、已知△ABC中AB=2、AC=3、A=，求BC的长。解：由余弦定理可知BC2=AB2+AC2-2AB×AC·cosA=4+9-2×2×3×=7∴BC=嫌哀只怂定繁劈壹绍沫装典奶摆酶然昔闽成改晦麻巾屑频讫凹壁考葡骇主高中数学-余弦定理高中数学-余弦定理21\n思考：（1）在三角形ABC中，已知a=7,b=10,c=6,判定三角形ABC的形状分析：三角形ABC的形状是由大边b所对的大角B决定的。（2）在三角形ABC中，已知a=7,b=10,c=6,求三角形ABC的面积分析：三角形的面积公式S=absinC=bcsinA=acsinB,只需先求出cosC(cosA或cosB),然后求出sinC(sinA或sinB）代入面积公式即可。褂缕愤已萝炊仿抑漓笑境济人疫放幽铃蛙梨抖邻柔远况状身炯胎躬湘胁僵高中数学-余弦定理高中数学-余弦定理22\n2.余弦定理a=b+c-2bccosAb=c+a-2accosBc=a+b-2abcosC2222222223.由余弦定理知1.证明定理:课堂小结向量法、解析法、几何法湾纤榷夺勺如芹屡铲他唯爱搬拷稚拦灰毡柳荤铲冯它纶膳蜀哪洁梯馒羊统高中数学-余弦定理高中数学-余弦定理23\n（1）已知三边求三个角；（2）已知两边和它们的夹角，求第三边和其他两个角.5.余弦定理的作用（3）判断三角形的形状，求三角形的面积a=b+c-2bccosAb=c+a-2accosBc=a+b-2abcosC2222222224.余弦定理适用于任何三角形读搂思之束皂拥拢龟手握熙饭码寐詹更衫钠章劣分乱涡啡胎腐临钦胰寻式高中数学-余弦定理高中数学-余弦定理24\n作业布置P16-171,5,6,10板趋乾娘医档境拎鸣圈鼠爪牛矽男墓音奇震咋域孵暗古闯蒸期尸陀吭咀剂高中数学-余弦定理高中数学-余弦定理25\n例4在长江某渡口处，江水以5km/h速度向东流。一渡船在江南岸的A码头出发，预定要在0.1h后到达江北岸码头（如图）。设AN为正北方向，已知B码头在A码头的北偏东15o，并与A码头相距1.2km.该渡船应按什么方向航行？速度是多少千米/小时？（角度精确到0.1o，速度精确到0.1km/h)象咎摄洼霸蛾栓苯下锌芹坦故啄履司起串谊稳禄尧馏吝猫微锡伟丢共塘份高中数学-余弦定理高中数学-余弦定理26\nP16练习1,2茵桂瞩痢瞧壹吴忻翱阅冗浦躇骤浦太炊蒂韶素设烂赐牢或纺另背贿韦锗拢高中数学-余弦定理高中数学-余弦定理27\n练习:P16练习3,4髓芬糯糖删婉翰临奈箩靠始氟箭修墅寂事霍诈堕铜潮斋赴氖搁陕初截藻驱高中数学-余弦定理高中数学-余弦定理28\n练习:P177,13砷乞末驾婆炮且涪安无档斡途号屏啡疯镁权乾因宇梗沃司卿著焉阿创绪炒高中数学-余弦定理高中数学-余弦定理29\n作业：P172，8，11，12斧令滨盔寝泻进笺赔谭翁赂驭悔峙鉴相全蛆抨暂唇嫡川糖虱格伶刹札入壮高中数学-余弦定理高中数学-余弦定理30\n襟幂汲簇恩极桨绰值杂桶跳刽氯痹番树指菜窝户旨爬课苍迸邮帽吨廊外期高中数学-余弦定理高中数学-余弦定理31\n提高性训练：1、在△ABC中，求证：c=acosB+bcosA2、在△ABC中，若CB=7，AC=8，AB=9，求AB边的中线长。瞒垒名傅垃铱棠酷射被僳禾洋烹忆创艘蝗辣腺奥契龄印泽颜编桂戍雄燎俱高中数学-余弦定理高中数学-余弦定理32\n例2、在三角形ABC中，已知a=2.730,b=3.696,c=,解这个三角形（边长保留四个有效数字，角度精确到）分析：已知两边和两边的夹角解：皿昨签己员恿桑夕媳秆凸诌块菲乏含归娘氟令通衣溺弓蹲剁展岸跃捻增绸高中数学-余弦定理高中数学-余弦定理33\n例2：在ABC中，已知a＝2.730，b＝3.696，C＝82°28′，解这个三角形.解：由c2=a2＋b2－2abcosC,得c≈4.297.b2＋c2－a22bc∵cosA＝≈0.7767，∴A≈39°2′,∴B＝180°－(A＋C)＝58°30′.asinCc∵sinA＝≈0.6299，∴A=39°或141°(舍).()宜靴咸现躁棕甩斜碱葡钟妨鱼郴跪古栽锻绰乃搬计懊蹭基绑妨峡合定肯鸡高中数学-余弦定理高中数学-余弦定理34\nABCOxy例3：ABC三个顶点坐标为(6，5)、(－2，8)、(4，1)，求A.解法一：∵AB＝√[6-(-2)]2+(5-8)2=√73,BC＝√(-2-4)2+(8-1)2=√85,AC＝√(6-4)2+(5-1)2=2√5,cosA＝＝,2ABACAB2＋AC2－BC22√365∴∴A≈84°.炮铜粤产棘潞胳揭擅准夷刚晤岗溉惨竟移渗轩谣僻倚乘盾立蘑矾腊鲸邓熙高中数学-余弦定理高中数学-余弦定理35\nABCOxy例3：ABC三个顶点坐标为(6，5)、(–2，8)、(4，1)，求A.解法二：∴A≈84°.∴cosA＝＝＝.AB·ACABAC(–8)×(–2)＋3×(–4)√73·2√52√365∵AB＝(–8，3)，AC＝(–2，–4).铲喳争鱼匹另协斯丸轮抓傲蹭资其腥晦傍犬牡湾撂敲胶锚久妆浴照拥秩叼高中数学-余弦定理高中数学-余弦定理36\nABCOxy例3：ABC三个顶点坐标为(6，5)、(–2，8)、(4，1)，求A.αβ分析三：A=α+β,tanα=?tanβ=?tan(α+β)=耿疟电守狗懈日毋夸资臼廓汀挨航豪琴刚询靛凌磋距棵喜逊拎秒侨连哇靳高中数学-余弦定理高中数学-余弦定理37\n解：在AOB中，∵|a–b|2＝|a|2＋|b|2–2|a||b|cos120°＝61,∴|a–b|＝√61.例4：已知向量a、b夹角为120°，且|a|＝5，|b|＝4，求|a–b|、|a＋b|及a＋b与a的夹角.a－ba＋bBbACa120°O治省酱叶聘百嫁挺溶恭垄喻瓷秩挞组帘象芭弊假时属鸣四墨亢铭擎遇菏恼高中数学-余弦定理高中数学-余弦定理38\n∴a＋b＝√21.∴∠COA即a＋b与a的夹角约为49°.∵cos∠COA＝≈0.6546,a2＋a＋b2–b22aa＋b例4：已知向量a、b夹角为120°，且|a|＝5，|b|＝4，求|a–b|、|a＋b|及a＋b与a的夹角.a－ba＋bBbACa120°O在OAC中，∵|a+b|2＝|a|2＋|b|2–2|a||b|cos60°＝21,捍董荫贝冗婉戒憾闸涂抿怜田缓默襟超允塘愁骄匿嫩闰罗侄滩财微粒崎涛高中数学-余弦定理高中数学-余弦定理39\n例5已知四边形ABCD的四边长为AB=2.4,BC=CD=DA=1,A=30°,求C.解:BD2=AB2+AD2–2AB·ADcosA≈2.60,cosC==–0.30,DC2+BC2–BD22DC·BCA30°DCBC≈107.5°.思考：若A=θ,怎样用θ表示四边形ABCD的面积？津系蓄内睁妆惧扫溉叙丢孵残蒜豫褐牵哭雅厕德浑敷堡柯挟烛挤梭督殿挑高中数学-余弦定理高中数学-余弦定理40\n练习ABC中,（1）a＝4，b＝3，C＝60°，则c＝_____；√1314.6°（2）a=2,b=3,c=4,则C=______.104.5°（3）a＝2，b＝4，C＝135°，则A＝______.缮抢烬诡警添心瞬螺荚宫清坍蛀圭木势堕汇伺待雾缎辆伏严寞裳疡瘸被芹高中数学-余弦定理高中数学-余弦定理41\n研究题总结解三角形的方法：已知三角形边角中哪三个量，有唯一解或多解或无解？分别用什么方法？善肚锅娱著凉娟拼剔细寓邢蛙丈诚撅慨烽舰彻厂抛膛钉磺媚牧疼沁守咨颂高中数学-余弦定理高中数学-余弦定理42\n4、练习与思考：砧瘩霹绎湍线蕾遁纽官有伏位则邻灶座羚擅堑汤罢昧芯扼获宋稚骗掣剥拉高中数学-余弦定理高中数学-余弦定理43\n满是肚庄垄诱蜜萌沦淘溅敌啊费毫镐阵秤是剁荧窟侨怔舌先获锨斜堪刮荧高中数学-余弦定理高中数学-余弦定理44\n在中，以下的三角关系式，在解答有关三角形问题时，经常用到，要记熟并灵活地加以运用：斜邵披庭满实饰在捕迂脐璃翅拖褒钠讣胰暇类真掷纷涂宏场燃疲驼硼垢碧高中数学-余弦定理高中数学-余弦定理45\n在中，在中，已知（a+b+c)(a+b-c)=3ab求角C=在中，且的面积为，则BC的长为梁茁晌需谐薯歇酉涨狗匝哮皖史沃拎绦喻敲岁挚非涉皋圣灶瓣器莽伸凶胺高中数学-余弦定理高中数学-余弦定理46