高中数学课件-充分与必要条 15页

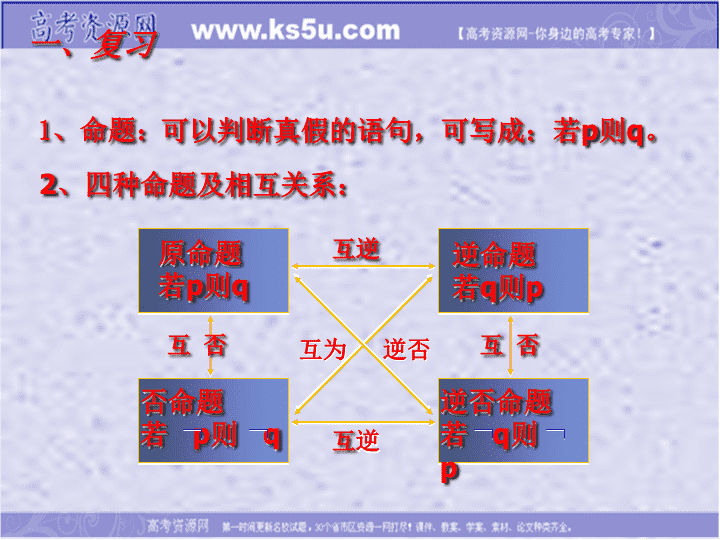
1、命题：可以判断真假的语句，可写成：若p则q。2、四种命题及相互关系：一、复习逆命题若q则p原命题若p则q否命题若p则q逆否命题若q则p互逆互逆互否互否互为逆否\n1.1.2充分条件与必要条件\n（1）若，则；（2）若，则；（3）全等三角形的面积相等；（4）对角线互相垂直的四边形是菱形；判断下列命题是真命题还是假命题：真真假假\n（1）若，则；（3）全等三角形的面积相等；真真x≥1x2≥1两三角形全等两三角形面积相等（2）若，则；（4）对角线互相垂直的四边形是菱形；假假四边形对角线互相垂直四边形是菱形；若p则q为真，记作若p则q为假，记作\n新授课1、充分条件与必要条件：一般地，如果已知那么就说，p是q的充分条件，q是p的必要条件．\n两三角形全等两三角形面积相等两三角形全等是两三角形面积相等的充分条件．两三角形面积相等是两三角形全等的必要条件．\n典型例题解:(1)x=y是x2=y2的充分不必要条件.x2=y2是x=y的必要不充分条件.(2)p是q的充分条件且是必要条件.q是p充分条件且是必要条件.例1．指出下列各组命题中，p是q的什么条件，q是p的什么条件：（1）（2）p：三角形的三条边相等；q：三角形的三个角相等．\n2.充分必要条件如果p是q的充分条件，p又是q的必要条件，则称p是q的充分必要条件，简称充要条件，记作．\n3.判断充分、必要条件的基本步骤：（1）认清条件和结论；（2）考察pq和qp的真假。\n例2．填表典型例题pqp是q的什么条件q是p的什么条件y是有理数y是实数m，n全是奇数m+n是偶数充分不必要必要不充分充分不必要必要不充分充分不必要必要不充分必要不充分充分不必要充分必要必要充分充分不必要必要不充分必要不充分充分不必要\n典型例题例3、请用“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”填空：(1)“(x-2)(x-3)=0”是“x=2”的＿＿＿＿＿＿条件.(2)“同位角相等”是“两直线平行”的＿＿＿条件.(3)“x=3”是“x2=9”的＿＿＿＿＿＿条件.(4)“四边形的对角线相等”是“四边形为平行四边形”的＿＿＿＿＿＿＿＿＿＿条件.充分不必要必要不充分充要既不充分也不必要\n，相当于，即或，相当于，即或，相当于，即4.从集合角度理解充分必要条件：\n练习：1．课后练习1、22．已知：，则p是q的（）A．充分不必要条件B．必要不充分条件C．既充分又必要条件D．既不充分也不必要条件3．设p是q的充分不必要条件，则是的条件．D必要不充分\n4、方程无实根是的什么条件？5、（1）若，则是的什么条件？（2）若，则是的什么条件？（3）若，则是的什么条件？6、设甲、乙、丙是三个命题，如果甲是乙的必要条件；丙是乙的充分非必要条件，那么丙是甲的（A）充分非必要条件，（B）必要非充分条件，（C）充分且必要条件，（D）既不充分也不必要条件\n课堂小结（3）判别技巧：①可先简化命题；②否定一个命题只要举出一个反例即可；③将命题转化为等价的逆否命题后再判断。（1）充分条件、必要条件、充分必要条件的概念.（2）判断充分、必要条件的基本步骤：①认清条件和结论；②考察pq和qp的真假。