高中物理平抛运动课件新人教版必修 13页

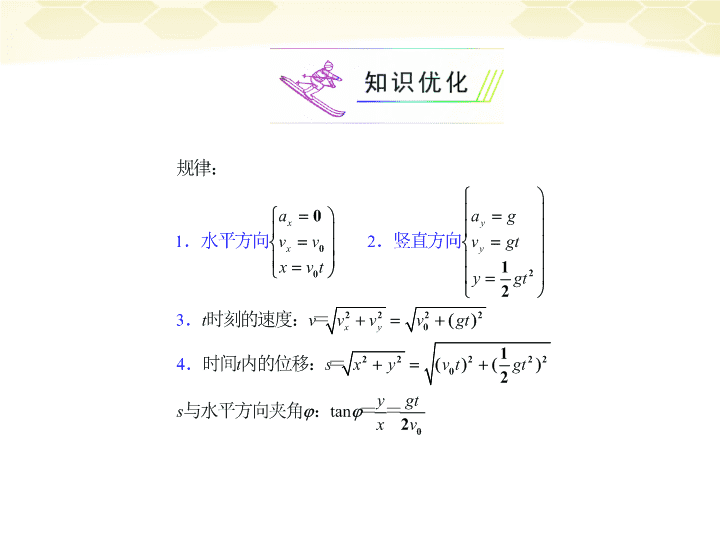
第2讲平抛运动\n\n\n\n\n落地点距抛出点的水平距离x＝v0t，由水平速度和下落时间共同决定．3．水平方向和竖直方向的两个分运动同时存在，互不影响，具有独立性．四、平抛运动的几个重要推论推论1：从抛出点开始，任意时刻速度偏向角的正切值等于位移偏向角的正切值的2倍．\n一、平抛运动规律应用例1、一水平放置的水管，距地面高h＝1.8m，管内截面积S＝2.0cm2.有水从管口以不变的速度v＝2.0m/s源源不断地沿水平方向射出，设水流稳定后在空中有多少立方米的水．\n变式训练1、(2010·北京)如图421，跳台滑雪运动员经过一段加速滑行后从O点水平飞出，经过3.0s落到斜坡上的A点．已知O点是斜坡的起点，斜坡与水平面的夹角θ＝37°，运动员的质量m＝50kg.不计空气阻力．(取sin37°＝0.60，cos37°＝0.80，g取10m/s2)求：(1)O点与A点的距离；(2)运动员离开O点时的速度；(3)运动员落到A点时的动能．图421\n\n二、两个角度关系例2、如图422所示，从倾角为θ的斜面上某点先后将同一小球以不同的初速度水平抛出，小球均落在斜面上．当抛出的速度为v1时，小球到达斜面时速度方向与斜面的夹角为α1；当抛出速度为v2时，小球到达斜面时速度方向与斜面的夹角为α2，则()A.当v1>v2时，α1>α2B.当v1>v2时，α1<α2C.无论v1、v2关系如何，均有α1＝α2D.α1、α2的关系与斜面倾角θ有关C图422\n\n变式训练2、在一倾角为α的斜面上A点将一小球以水平初速v0抛出，落在斜面上的B点，不计空气阻力，如图423，求：(1)物体飞行的时间；(2)从抛出到离斜面最远所用时间？图423\n