人教版高中数学必修4课件全册精品课件 181页

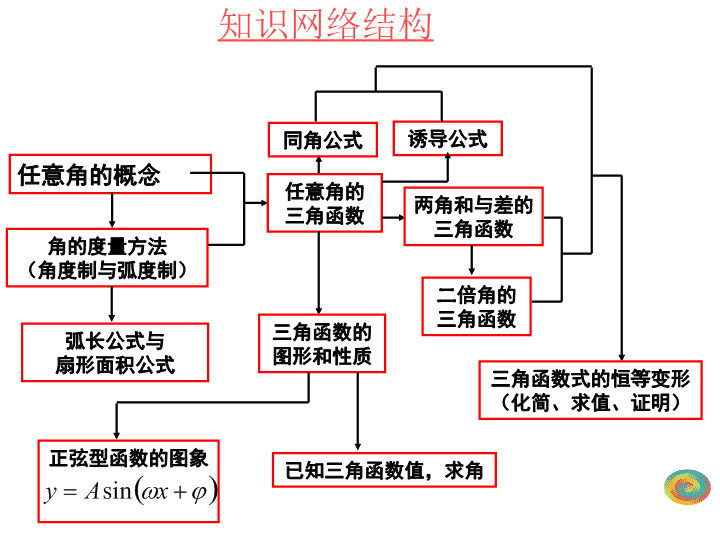
2021年7月29日高中数学必修四课件全册（人教A版）\n任意角的概念角的度量方法（角度制与弧度制）弧长公式与扇形面积公式任意角的三角函数同角公式诱导公式两角和与差的三角函数二倍角的三角函数三角函数式的恒等变形（化简、求值、证明）三角函数的图形和性质正弦型函数的图象已知三角函数值，求角知识网络结构\n1.角的概念的推广（1）正角，负角和零角.用旋转的观点定义角，并规定了旋转的正方向，就出现了正角，负角和零角，这样角的大小就不再限于00到3600的范围.（3）终边相同的角，具有共同的绐边和终边的角叫终边相同的角，所有与角终边相同的角（包含角在内）的集合为.（4）角在“到”范围内，指.（2）象限角和轴线角.象限角的前提是角的顶点与直角坐标系中的坐标原点重合，始边与轴的非负半轴重合，这样当角的终边在第几象限，就说这个角是第几象限的角，若角的终边与坐标轴重合，这个角不属于任一象限，这时也称该角为轴线角.一、基本概念：\n一、任意角的三角函数1、角的概念的推广正角负角oxy的终边的终边零角\n二、象限角：注：如果角的终边在坐标轴上，则该角不是象限角。三、所有与角终边相同的角，连同角在内，构成集合：（角度制）（弧度制）例1、求在到（）范围内，与下列各角终边相同的角原点x轴的非负半轴一、在直角坐标系内讨论角，角的顶点与重合，角的始边与重合。逆时针旋转为正，顺时针旋转为负。角的终边（除端点外）在第几象限，我们就说这个角是第几象限角。\n1、终边相同的角与相等角的区别终边相同的角不一定相等，相等的角终边一定相同。2、象限角、象间角与区间角的区别3、角的终边落在“射线上”、“直线上”及“互相垂直的两条直线上”的一般表示式三、终边相同的角\n(1)与角终边相同的角的集合:1.几类特殊角的表示方法{|=2k+,k∈Z}.(2)象限角、象限界角(轴线角)①象限角第一象限角:(2k<<2k+,kZ)2第二象限角:(2k+<<2k+,kZ)2第三象限角:(2k+<<2k+,kZ)23第四象限角:2(2k+<<2k+2,kZ或2k-<<2k,kZ)23一、角的基本概念\n②轴线角x轴的非负半轴:=k360º(2k)(kZ);x轴的非正半轴:=k360º+180º(2k+)(kZ);y轴的非负半轴:=k360º+90º(2k+)(kZ);2y轴的非正半轴:=k360º+270º(2k+)或=k360º-90º(2k-)(kZ);232x轴:=k180º(k)(kZ);y轴:=k180º+90º(k+)(kZ);2坐标轴:=k90º()(kZ).2k\n例2、（1）、终边落在x轴上的角度集合：（2）、终边落在y轴上的角度集合：（3）、终边落在象限平分线上的角度集合：\n典型例题各个象限的半角范围可以用下图记忆，图中的Ⅰ、Ⅱ、Ⅲ、Ⅳ分别指第一、二、三、四象限角的半角范围；例1.若α是第三象限的角，问α/2是哪个象限的角?2α是哪个象限的角?\n高考试题精选及分析C点评:本题先由α所在象限确定α/2所在象限,再α/2的余弦符号确定结论.\n例1求经过1小时20分钟时钟的分针所转过的角度：解：分针所转过的角度例2已知a是第二象限角，判断下列各角是第几象限角（1）（2）评析：在解选择题或填空题时，如求角所在象限，也可以不讨论k的几种情况，如图所示利用图形来判断.\n四、什么是1弧度的角？长度等于半径长的弧所对的圆心角。OABrr2rOABr\n（3）角度与弧度的换算.只要记住，就可以方便地进行换算.应熟记一些特殊角的度数和弧度数.在书写时注意不要同时混用角度制和弧度制（4）弧长公式和扇形面积公式.\n度弧度02、角度与弧度的互化特殊角的角度数与弧度数的对应表\n略解：例3．已知角和满足求角–的范围.解：例4、已知扇形的周长为定值100，问扇形的半径和圆心角分别为多少时扇形面积最大？最大值是多少？扇形面积最大值为625.\n例7.已知一扇形中心角是α，所在圆的半径是R.①若α＝60°，R＝10cm，求扇形的弧长及该弧所在的弓形面积.②若扇形的周长是一定值C(C＞0)，当α为多少弧度时，该扇形的面积有最大值?并求出这一最大值?指导:扇形的弧长和面积计算公式都有角度制和弧度制两种给出的方式，但其中用弧度制给出的形式不仅易记，而且好用.在使用时，先要将问题中涉及到的角度换算为弧度.\n解：（1）设弧长为l，弓形面积为S弓。（2）扇形周长C=2R+l=2R+\n正弦线：余弦线：正切线：（2）当角α的终边在x轴上时，正弦线，正切线变成一个点；当角α的终边在y轴上时，余弦线变成一个点，正切线不存在。2.正弦线、余弦线、正切线xyOPTMA有向线段MP有向线段OM有向线段AT注意：（1）圆心在原点，半径为单位长的圆叫单位圆.在平面直角坐标系中引进正弦线、余弦线和正切线\n三角函数三角函数线正弦函数余弦函数正切函数正弦线MP正弦、余弦函数的图象yxxO-1PMA(1,0)Tsin=MPcos=OMtan=AT注意：三角函数线是有向线段！余弦线OM正切线AT\nPOMPOMPOMPOMMP为角的正弦线,OM为角的余弦线为第二象限角时为第一象限角时为第三象限角时为第四象限角时\n10）函数y=lgsinx+的定义域是（A）（A）{x|2kπ0,ω>0)的图象的对称中心和对称轴方程\n2、函数的图象（A>0,>0)第一种变换:图象向左()或向右()平移个单位横坐标伸长()或缩短()到原来的倍纵坐标不变纵坐标伸长(A>1)或缩短(01)或缩短(00,|φ|<)的图象向左平移个单位，再数将图象上所有点的横坐标扩大到原来2倍（纵坐标不变）得函数y=sinx图象则ω=____φ=____。解：y=sin2x=sin2(x-)=sin(2x-)ω=2φ=-\n7、8、\n思路:函数y=sin2x+acos2x可化为要使它的图象关于直线x=-π/8对称,则图象在该处必是处于波峰或波谷.即函数在x=-π/8时取得最大、小值.\n\n例9、(98年)关于函数有下列命题：①的表达式可改写为②是以为最小正周期的周期函数③的图象关于点对称④的图象关于直线对称其中正确的命题序号是。①③\n（3）连线：用“五点作图法”作出y=Asin(x+)在长度为一个周期闭区间上的图象(2)描点：（1）列表：0-A0A0y0x+xy(,0)(,A)(,0)(,-A)(,0)\n(1)由最大值点（或最小值点）定A(2)由两个关键点（特殊点）定和总结给出函数y=Asin(x+)(A>0,>0)的图象求其解析式的一般方法：\n6、已知下图是函数的图象(1)求的值；(2)求函数图象的对称轴方程.Ox21–1–2y⑴（2）函数图象的对称轴方程为即\n\n设函数（1）求；（2）求函数的单调递增区间；（3）画出函数在区间[0，π]上的图象.图象的一条对称轴是直线\n解析:（1）图象的一条对称轴,是Oyx\n（2）函数的单调递增区间为\nxyπo-11x∈[0,π]（3）\n5)函数(A>0,>0)的一个周期内的图象如图，则有()(A)(B)(C)(D)\nyx03-3yx02-2-4如图：根据函数y=Asin(x+)(A>0,>0)图象求它的解析式\nyx0-44如图：根据函数y=Asin(x+)(A>0,>0)图象求它的解析式\nyx02-2如图：根据函数y=Asin(x+)(A>0,>0)图象求它的解析式\nyx012如图：根据函数y=2sin(x+)(>0)图象求它的解析式\nyx012如图：根据函数y=2sin(x+)(>0)图象求它的解析式\nyx根据正弦函数的图象和性质寻找区间使其满足：使符合条件的的角x有且只有一个，而且包括锐角．4.11已知三角函数值求角在闭区间上，符合条件的角x，叫做实数a的反正弦，记作，即，其中，且．的意义：首先表示一个角，角的正弦值为a，即．角的范围是\n4.11已知三角函数值求角练习：（1）表示什么意思？表示上正弦值等于的那个角，即角，故（2）若，则x=（3）若，则x=\n4.11已知三角函数值求角的意义：首先表示一个角，角的余弦值为a，即．角的范围是．根据余弦函数的图象和性质寻找区间使其满足：使符合条件的的角x有且只有一个，而且包括锐角．yx在闭区间上，符合条件的角x，叫做实数a的反余弦，记作，即，其中，且．\n4、已知三角函数值求角y=sinx,的反函数y=arcsinx,y=cosx,的反函数y=arccosx,y=tanx,的反函数y=arctanx,⑵已知角x()的三角函数值求x的步骤①先确定x是第几象限角②若x的三角函数值为正的，求出对应的锐角；若x的三角函数值为负的，求出与其绝对值对应的锐角③根据x是第几象限角，求出x若x为第二象限角，即得x=；若x为第三象限角，即得x=；若x为第四象限角，即得x=④若，则在上面的基础上加上相应函数的周期的整数倍。⑴反三角函数\n已知三角函数值求角已知三角函数值求角x（仅限于[0，2π]）的解题步骤：1、如果函数值为正数，则求出对应的锐角x0；如果函数值为负数，则求出与其绝对值相对应的锐角x0；2、由函数值的符号决定角x可能的象限角；3、根据角x的可能的象限角得出[0，2π]内对应的角：如果x是第二象限角，那么可以表示为π－x0如果x是第三象限角，那么可以表示为π＋x0如果x是第四象限角，那么可以表示为2π－x0\n说明:三角函数值求角，关键在于角所属范围，这点不容忽视.(1)判断角的象限；(2)求对应锐角；如果函数值为正数，则先求出对应的锐角x1；如果函数值为负数，则先求出与其绝对值对应的锐角x1.(3)求出(0，2π)内对应的角；如果它是第二象限角，那么可表示为－x1＋π；如果它是第三或第四象限角，则可表示为x1＋π或－x1＋2π.(4)求出一般解利用终边相同的角有相同的三角函数值这一规律写出结果.（三）已知三角函数值求角”的基本步骤1、基本步骤\n2、表示角的一种方法——反三角函数法1、反正弦：这时sin(arcsina)=a2、反余弦：这时cos(arccosa)=a这时tan(arctana)=a3、反正切：\n三、两角和与差的三角函数1、预备知识：两点间距离公式xyo●●2、两角和与差的三角函数注：公式的逆用及变形的应用公式变形\n3、倍角公式\n一、知识点（一）两角和与差公式（二）倍角公式★公式=1-cos2α2cos2α=1+cos2α1+cos2α=2cos2α1-cos2α=2sin2αtanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)注意1、公式的变形如：注意2、公式成立的条件（使等式两边都有意义）.Cα±β：Sα±β：C2α：S2α：T2α：Tα±β：\n倍角公式：注：正弦与余弦的倍角公式的逆用实质上就是降幂的过程。特别和角公式的一个重要变形\n其它公式1、半角公式2、万能公式\n二、两角和与差的正弦、余弦、正切：注意：、的变形式以及运用和差公式时要会拼角如：要熟悉公式逆用！\n三、一个化同角同函数名的常用方法：如：例、求的值四、二倍角公式：\n降幂（扩角）公式升幂（缩角）公式和差化积公式：积化和差公式：\n例4．化简：解法1：从“角”入手，“复角”化为“单角”，利用“升幂公式”。\n例4．化简：解法2：从“幂”入手，利用“降幂公式”。\n例4．化简：解法3：从“名”入手，“异名化同名”。\n例4．化简：解法4：从“形”入手，利用“配方法”。\n三角解题常规宏观思路分析差异寻找联系促进转化指角的、函数的、运算的差异利用有关公式，建立差异间关系活用公式，差异转化，矛盾统一\n微观直觉1、以变角为主线，注意配凑和转化；2、见切割，想化弦；个别情况弦化切；3、见和差，想化积；见乘积，化和差；4、见分式，想通分，使分母最简；5、见平方想降幂，见“1±cosα”想升幂；6、见sin2α，想拆成2sinαcosα；7、见sinα±cosα或9、见cosα·cosβ·cosθ····，先运用sinα+sinβ=pcosα+cosβ=q8、见asinα+bcosα，想化为的形式若不行，则化和差10、见cosα+cos(α+β)+cos(α+2β)…，想乘想两边平方或和差化积\n总结：多种名称想切化弦；遇高次就降次消元；asinA+bcosA提系数转换；多角凑和差倍半可算；难的问题隐含要显现；任意变元可试特值算；求值问题缩角是关键；字母问题讨论想优先；非特殊角问题想特角算；周期问题化三个一再算；适时联想联想是关键！\n【解题回顾】找出非特殊角和特殊角之间的关系,这种技巧在化简求值中经常用到，并且三角式变形有规律即坚持“四化”：多角同角化异名同名化切割弦化特值特角互化\n公式体系的推导：首先利用两点间的距离公式推导，然后利用换元及等价转化等思想方法，以为中心推导公式体系。\nsin²α+cos²α=1\n二【述评】1、变为主线，抓好训练。变是本章的主题，在三角变换考查中，角的变换（恒等）、三角函数名的变换（诱导公式）、三角函数次数的变换（升、降幂公式）、三角函数表达式的变换（综合）等比比皆是。在训练中，强化变化意识是关键。但题目不可以太难。较特殊技巧的题目不做。立足课本，掌握课本中常见问题的解法，把课本中的习题进行归类，并进行分析比较，寻找解题规律。2、基本解题规律：观察差异（角或函数或运算）寻找联系（借助于熟知的公式、方法或技巧）分析综合（由因导果或执果索因）实现转化。\n1、值域与最值问题①利用有界性②化二次函数型③运用合一变换④换元\n十七、求值域问题：主要是将式子化成同角度同函数名的形式，再利用正弦函数与余弦函数的有界性求解。例10、求函数的值域有时还要运用到的关系\n2、对称性问题3、奇偶性与周期性问题注意绝对值的影响化为单一三角函数\n4、单调性与单调区间复后函数单调性注意负号的处理\n5、图像变换问题①相位变换、周期变换、振幅变换②求函数解析式\n例5:已知函数求：⑴函数的最小正周期；⑵函数的单增区间；解：⑴⑵应用：化同一个角同一个函数\n例5:已知函数求：⑶函数的最大值及相应的x的值；⑷函数的图象可以由函数的图象经过怎样的变换得到。解：⑶⑷图象向左平移个单位图象向上平移2个单位应用：化同一个角同一个函数\n例6：已知解：应用：化简求值\n例1化简：解:∵∴原式=\n\n\n练习题\n例2(1)已知求证：(2)已知求(1)证明：∴∴化简得：∴∵\n(2)已知求解:∵∴∵∴∵∴∴\n解：应用：化简求值例5.已知\n∵∴∴\n2、解:由两边平方得:①2由两边平方得:②2由①2+②2得:即所以由②2－①2得:\n\n\n练习已知求解:∵∴∵∴∴∴\n\n例3.已知函数f(x)＝sin(2x－)＋2sin2(x－)(x∈R)．（1）求函数f(x)的最小正周期；（2）求使函数f(x)取最大值的x的集合．\n解：f(x)＝sin(2x－)＋1－cos2(x－)＝sin(2x－)－cos(2x－)＋1＝2sin(2x－)＋1．函数f(x)的最小正周期T＝.使函数f(x)取最大值的x的集合为{x|x=k＋,k∈Z}．\n5、已知f(x)=2sin(x+)cos(x+)+2cos2(x+)-。（1）化简f(x)的解析式；（2）若0≤θ≤π，求θ，使函数f(x)为偶函数。（3）在（2）成立的条件下，求满足f(x)=1，x∈[-π,π]的x的集合。解：(1)f(x)=sin(2x+θ)+[2cos2(x+)-1]=sin(2x+θ)+cos(2x+θ)=2cos(2x+θ-)(2)当θ=时f(x)为偶函数。(3)2cos2x=1cos2x=x=±或x=±\n例6、已知函数f(x)=sin(x+)+sin(x-)+cosx+a(a∈R,a常数)。（1）求函数f(x)的最小正周期；（2）若x∈[-,]时，f(x)的最大值为1，求a的值。解：（1）f(x)=sin(x+)+sin(x-)+cosx+a=sinx+cosx+a=2sin(x+)+a∴f(x)最小正周期T=2（2）x[-,]∴x+∈[-,]∴f(x)大=2+a∴a=-1\n例7、求函数的值域.解：又∵-1≤sinx≤1∴原函数的值域为：变题：已知函数（a为常数，且a＜0），求该函数的最小值.当-2≤＜0时，当＜-2时，\n1、已知a>0函数y=-acos2x-asin2x+2a+bx∈[0,]，若函数的值域为[-5,1]，求常数a,b的值。解：3a+b=1∴a=2b=-5b=-5\n2、函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a)(a∈R)：（1）求g(a)；（2）若g(a)=，求a及此时f(x)的最大值。解：（1）f(x)=2(cosx-)2-2-2a-1-1≤cosx≤1①当-1≤≤1即-2≤a≤2时f(x)小=-2-a-1②当>1即a>2时f(x)小=f(1)=1-4a③当<-1即a<-2时f(x)小=f(-1)=1\n（2）a=-1此时f(x)=2(cosx+)2+f(x)大=52、函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a)(a∈R)：（1）求g(a)；（2）若g(a)=，求a及此时f(x)的最大值。\n3、已知f(x)=2sin(x+)cos(x+)+2cos2(x+)-。（1）化简f(x)的解析式；（2）若0≤θ≤π，求θ，使函数f(x)为偶函数。（3）在（2）成立的条件下，求满足f(x)=1，x∈[-π,π]的x的集合。解：(1)f(x)=sin(2x+θ)+[2cos2(x+)-1]=sin(2x+θ)+cos(2x+θ)=2cos(2x+θ-)(2)当θ=时f(x)为偶函数。(3)2cos2x=1cos2x=x=±或x=±\n例4.已知函数f(x)＝asinx－bcosx（a，b为常数，a≠0，x∈R）在x＝处取得最小值，则函数y＝f(－x)的对称中心坐标是____________．\n解：由(a－b)＝－化简得a＝－b．所以f(x)＝asin(x＋)，a＜0．从而f(－x)＝asinx，其对称中心坐标为(k，0)，k∈Z.\n平面向量复习向量的三种表示表示运算向量加法与减法向量的相关概念实数与向量的积三角形法则平行四边形法则向量平行、垂直的条件平面向量的基本定理平面向量向量的数量积向量的应用\n几何表示:有向线段向量的表示字母表示坐标表示:(x，y)若A(x1,y1),B(x2,y2)则AB=(x2－x1,y2－y1)返回\n1.向量的概念:2.向量的表示:3.零向量:4.单位向量:5.平行向量:6.相等向量:7.共线向量:既有大小又有方向的量1.有向线段2.字母3.有向线段起点和终点字母长度为零的向量(零向量与任意向量都平行长度为1个单位的向量1.方向相同或相反的非零向量2.零向量与任一向量平行长度相等且方向相同的向量平行向量就是共线向量\n向量的模（长度）1.设a=(x,y),则2.若表示向量a的起点和终点的坐标分别为A(x1,y1)、B(x2,y2)，则返回\n\n例1：思考下列问题：1、下列命题正确的是（1）共线向量都相等（2）单位向量都相等（3）平行向量不一定是共线向量（4）零向量与任一向量平行四、例题\n一、第一层次知识回顾：1.向量的加法运算OAB三角形法则OABC平行四边形法则坐标运算设：则“首尾相接首尾连”\n2.向量的减法运算1）减法法则：OAB2）坐标运算设：则设则思考：若非零向量，则它们的模相等且方向相同。同样若：“同始点尾尾相接,指向被减向量”一、第一层次知识回顾：\n1.向量的加法运算ABCAB+BC=三角形法则OABCOA+OB=平行四边形法则坐标运算:则a+b=重要结论：AB+BC+CA=0设a=(x1,y1),b=(x2,y2)(x1+x2,y1+y2)ACOC\n例题：\n实数λ与向量a的积定义：坐标运算：其实质就是向量的伸长或缩短！λa是一个向量.它的长度|λa|=|λ||a|；它的方向(1)当λ≥0时,λa的方向与a方向相同；(2)当λ＜0时,λa的方向与a方向相反.若a=(x,y),则λa=λ(x,y)=(λx,λy)返回\n平面向量的数量积（1）a与b的夹角：（2）向量夹角的范围：（3）向量垂直：[00，1800]abθ共同的起点aOABbθOABOABOABOAB\n（4）两个非零向量的数量积：规定：零向量与任一向量的数量积为0a·b=|a||b|cosθ几何意义：数量积a·b等于a的长度|a|与b在a的方向上的投影|b|cosθ的乘积。AabθBB1OBAθbB1aOθBb(B1)AaO若a=(x1,y1),b=(x2,y2)则a·b=x1·x2+y1·y2\n5、数量积的运算律：⑴交换律：⑵对数乘的结合律：⑶分配律：注意：数量积不满足结合律返回\n3.平面向量的数量积的性质(1)a⊥ba·b＝0(2)a·b＝±|a|·|b|(a与b同向取正，反向取负)(3)a·a＝|a|2或|a|＝√a·a(4)(5)|a·b|≤|a||b|4.平面向量的数量积的坐标表示(1)设a＝(x1，y1)，b＝(x2，y2)，则a·b＝x1x2+y1y2，|a|2＝x21+y21，|a|＝√x21+y21，a⊥b<=>x1x2+y1y2＝0(2)(3)设a起点(x1，y1),终点(x2，y2)则\n5、重要定理和公式：⑵⑶设则⑷设两点则⑸设则⑴设非零向量则\n二、平面向量之间关系向量平行(共线)条件的两种形式:向量垂直条件的两种形式:\n（3）两个向量相等的条件是两个向量的坐标相等.即:那么\n3、平面向量的坐标运算—知识回忆（1）e1、e2不共线，a=λ1e1+λ2e2(存在一对实数λ1，λ2)(λ1，λ2唯一的)。（2）a=xi+yj(x,y)为a的直角坐标，a=(x,y)（3）①若a=(x1,y1)b=(x2,y2)，则a±b=(x1±x2,y1±y2)②A(x1,y1)B(x2,y2)AB=(x2-x1,y2-y1)③若a=(x,y)则λa=(λx,λy)④a=(x1,y1)b=(x2,y2)(b≠0)a∥bx1y2-x2y1=0知识回忆典例分析例5例6回目录\n例题解这个方程组得k=-(1/3),λ=-(1/3),即当k=-(1/3)时，ka+b与a-3b平行，这时ka+b=-a/3+b.因为λ=-(1/3)<0,所以-a/3+b与a-3b反向。在本例中，也可以根据向量平行充分条件的坐标形式，从(k-3)(-4)-10(2k+2)=0,先解出k=-(1/3)，然后再求λ。注\n例2设a，b是两个不共线向量。AB=2a+kbBC=a+bCD=a-2bA、B、D共线则k=_____(k∈R)解：BD=BC+CD=a+b+a-2b=2a-b2a+kb=λ(2a-b)=2λa-λb2=2λλ=-1k=-λk=-1∴k=-1∴知识回忆典例分析例2例3例42、实数与向量的积—典例分析-例2本页结束回目录\n1．与平面几何的结合：ABDCABDC四边形ABCD是菱形四边形ABCD是矩形\nABCOABCDMABCOM外心重心重心\n第一层次例题分析类型四：三角形中的向量问题重要结论：ABCO\n第一层次例题分析类型四：三角形中的向量问题\n练习1：判断正误，并简述理由。(√）(√）(√）(×）(×）(×）\n平面向量复习2.设AB=2(a+5b)，BC=2a+8b，CD=3(ab)，求证：A、B、D三点共线。分析要证A、B、D三点共线，可证AB=λBD关键是找到λ解：∵BD=BC+CD=2a+8b+3(ab)=a+5b∴AB=2BD且AB与BD有公共点B∴A、B、D三点共线AB∥BD