人教版高中数学课件：函数的单调性 9页

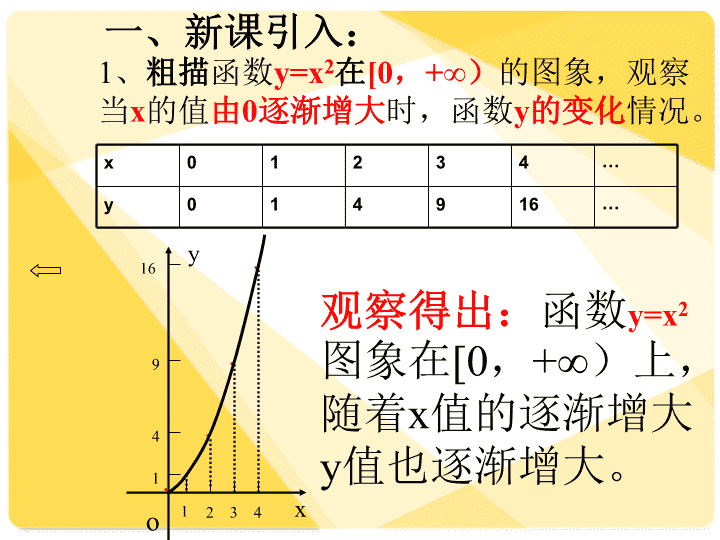
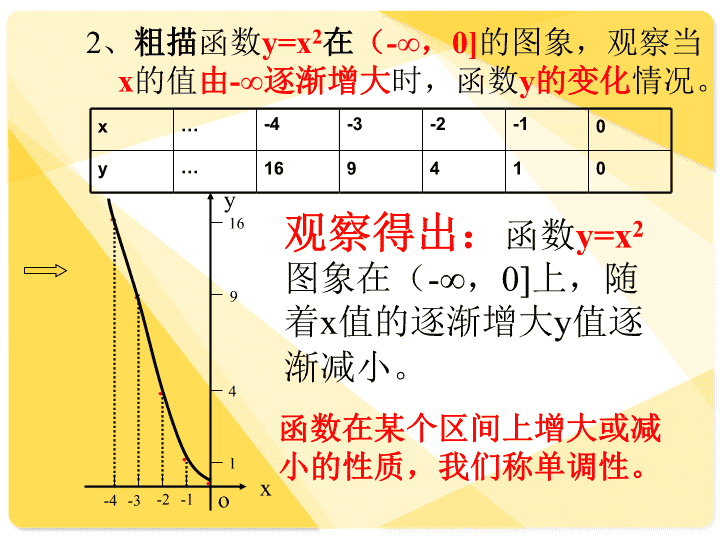
第四章函数4.6函数的单调性秦皇岛市职业技术学校李天乐\nx01234…y014916…一、新课引入：1、粗描函数y=x2在[0，+∞）的图象，观察当x的值由0逐渐增大时，函数y的变化情况。●●●●o916411234yx●观察得出：函数y=x2图象在[0，+∞）上，随着x值的逐渐增大y值也逐渐增大。\n2、粗描函数y=x2在（-∞，0]的图象，观察当x的值由-∞逐渐增大时，函数y的变化情况。x…-4-3-2-10y…1694101xyo4916-1-2-3-4●●●●●观察得出：函数y=x2图象在（-∞，0]上，随着x值的逐渐增大y值逐渐减小。函数在某个区间上增大或减小的性质，我们称单调性。\n二、新课1、函数单调性的定义：一般地，对于给定区间上的函数f（x）：（1）如果对于属于这个区间的自变量的任意两个值x1、x2，当x1＜x2时，都有f（x1）＜f（x2），那么就说函数f（x）在这个区间上是增函数。（2）如果对于属于这个区间的自变量的任意两个值x1、x2，当x1＜x2时，都有f（x1）＞f（x2），那么就说函数f（x）在这个区间上是减函数。\n2、单调函数和单调区间：如果函数f（x）在某个区间上是增函数或者减函数，那么就说函数f（x）在这个区间上是单调函数。这个区间叫做函数f（x）的单调区间。0xyy=f（x）x1x2f（x1）f（x2）由左向右，沿函数图象运动，上坡增，下坡减。y=f（x）x1x2f（x1）f（x2）y0x\n例1、根据函数f（x）的图象（包括端点），指出这个函数的单调区间，以及在每一个单调区间上函数是增函数还是减函数。单调区间[-2，0.9],[2，3]上单调区间[-3，-2],[0.9，2]上定义域：[-3，3]解：y=f（x）-3-2-10.923xy0增函数减函数单调增区间单调减区间\n练习：根据函数f（x）的图象（包括端点），指出这个函数的单调区间，以及在每一个单调区间上函数是增函数还是减函数。y=f（x）-22-0xy\n例2：判断函数f（x）=2x+1在区间（-∞，+∞）上的单调性。解：根据函数单调性定义，设x1，x2是区间（-∞，+∞）内的任意两个实数，并且x1＜x2，那么f（x1）=2x1+1f（x2）=2x2+1f（x1）－f（x2）=（2x1+1）-（2x2+1）=2（x1-x2）因为x1＜x2，则x1-x2＜0，所以:f（x1）－f（x2）＜0即f（x1）＜f（x2）因此函数f（x）=2x+1在区间（-∞，+∞）上是增函数。\n小结：2、对于给定区间内的函数：增函数（1）x1＜x2f（x1）＜f（x2）自变量和函数值大小一致，为增函数。减函数（1）x1＜x2f（x1）＞f（x2）自变量和函数值大小相反，为减函数。（重点）1、单调函数{增函数减函数单调区间{单调增区间单调减区间函数在某个区间上是增函数，这个区间叫做函数的单调增区间；函数在某个区间上是减函数，这个区间叫做函数的单调减区间（重点）{3、判定函数f（x）在给定区间上的单调性，应在给定区间内任意选定两变量x1，x2，用差f（x1）-f（x2）来确定f（x1），f（x2）的大小关系。进而判断函数在给定区间内是增函数还是减函数。（难点）