高中数学 函数的极限范例例题课件 23页

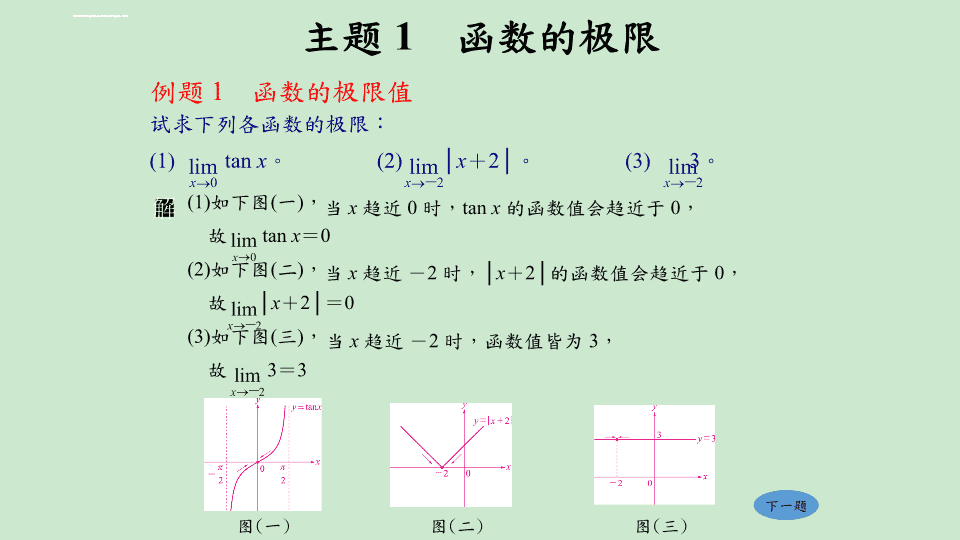
主题1函数的极限例题1函数的极限值(1)如下图(一)，故tanx＝0(2)如下图(二)，故│x＋2│＝0(3)如下图(三)，故3＝3试求下列各函数的极限：(1)tanx。(2)│x＋2│。(3)3。下一题图(一)图(三)图(二)当x趋近0时，tanx的函数值会趋近于0，当x趋近－2时，│x＋2│的函数值会趋近于0，当x趋近－2时，函数值皆为3，\n因为x由左边或右边趋近－1时，f（x）皆趋近2故极限值为2（注意：虽然f（－1）＝3，但极限值和此函数值无关）例题2由图形判断函数的极限值(一)因为x由左边趋近－3时，f（x）趋近0而x由右边趋近－3时，f（x）也趋近0，故极限值为0函数f（x）的图形如右，试求：上一题下一题因为x由左边趋近－2时，f（x）趋近1而x由右边趋近－2时，f（x）趋近2，两者不相等\n例题3由图形判断函数的极限值(二)f（x）＝试绘出f（x）＝的函数图形，并求上一题下一题∴f（x）＝的图形与f（x）＝x＋3的图形如右图所示＝x＋3（当x3）在x3时皆相同\n例题4左极限与右极限(1)y＝f（x）的函数图形如右：①当x＜0时，②当x＞0时，设f（x）＝　，则：上一题下一题(1)试求(2)利用左极限及右极限的概念说明　　　　是否存在。\n例题5极限的存在(1)如右图，故[x]＝－2当x由右侧趋近－1时，[x]＝－1，故[x]＝－1因左极限不等于右极限，利用左极限及右极限判断下列极限是否存在。(1)[x]。当x由左侧趋近－1时，[x]＝－2，故[x]不存在\n例题5极限的存在(2)如右图，利用左极限及右极限判断下列极限是否存在。\n例题5极限的存在(3)如右图，(3)log2│x│。上一题下一题左极限与右极限均不存在利用左极限及右极限判断下列极限是否存在。\n例题6函数极限的运算性质(一)计算下列各极限：(1)(2)(1)(2)\n例题6函数极限的运算性质(一)计算下列各极限：上一题下一题\n例题7函数极限的运算性质(二)分数型计算下列各极限：(1)(1)x→1表示x1∴x－10\n例题7函数极限的运算性质(二)分数型计算下列各极限：(2)x→0时，（2x－1）→－1，即当x在0附近时2x－1＜0x→0时，（x2－x＋1）→1，即当x在0附近时x2－x＋1＞0上一题下一题(2)\n例题8函数极限的运算性质(三)合并型上一题下一题\n例题9函数极限的运算性质(四)根式型计算下列各极限：(1)(1)\n例题9函数极限的运算性质(四)根式型计算下列各极限：上一题下一题(2)(2)\n例题10利用函数极限的性质解未知数上一题下一题∴9a＋3b＋3＝03a＋b＋1＝0b＝－3a－1…………（＊）可得ax2＋bx＋3＝ax2＋（－3a－1）x＋3代回（＊）式中，得b＝－4＝ax2－3ax－x＋3＝（ax－1）（x－3）∴\n例题11多项式因式的判断上一题下一题故f（x）＝（x－1）（x－2）（x－3）\n例题12夹挤定理求函数的极限值上一题下一题\n主题2连续函数例题13函数连续的范围(1)x2－1＝0∴f（x）在x＝±1时，函数值不存在故f（x）在区间（－∞,－1），（－1,1），（1,∞）连续(2)函数图形如右所示：f（x）在区间（－∞,1），（1,∞）连续试求下列各函数连续的范围：上一题下一题（x＋1）（x－1）＝0x＝±1\n例题14函数不连续的点但f（2）＝2即极限值不等于函数值，故f（x）在x＝2时并不连续，图形如右所示，试问f（x）在x＝2是否连续？若不连续，上一题下一题应如何定义f（x），使得f（x）是连续函数？\n例题15连续函数②f(x)＝x2＝0，f(x)＝　（ax＋b）＝b∴b＝0由①与②得上一题下一题在x＞2，0＜x＜2，x＜0时，今在x＝2与x＝0时也要连续，必须有f(x)＝f(2)与f(x)＝f（0）①f(x)＝　（ax＋b）＝2a＋b，f(x)＝　（2－x2）＝－2∴2a＋b＝－2函数分别为多项式函数，故为连续由连续的定义，是连续函数，试求a与b的值。\n主题3中间值定理例题16中间值定理的应用上一题试利用中间值定理与函数f（x）＝x3，来说明存在一正实数，其立方等于4。多项式函数f（x）＝x3为连续函数因为f（1）＝1，f（2）＝8，而4介于1与8之间故由中间值定理，在区间（1,2）中，必存在一正实数c下一题\n例题17勘根定理的应用(1)令F（x）＝f（x）＋g（x）－x＝2x4＋x2－x－10(1)设f（x）＝2x4－5，g（x）＝x2－5，试证在1与2之间有一实数c，满足f（c）＋g（c）＝c。＝（2x4－5）＋（x2－5）－x在1与2之间有一实数c满足F（c）＝0f（c）＋g（c）＝cF（1）＝2＋1－1－10＝－8＜0F（2）＝2．24＋22－2－10＝24＞0∴F（1）．F（2）＜0由勘根定理可知，即f（c）＋g（c）－c＝0\n例题17勘根定理的应用(2)令f（x）＝x．2x－1024∵y＝x与y＝2x都是连续函数∴f（x）也是连续函数f（7）＝7．27－1024＝－128＜0f（8）＝8．28－1024＝1024＞0∴f（7）．f（8）＜0由勘根定理可知，f（x）＝0在7与8之间有正根故n＝7(2)设方程式x．2x＝1024有一正根介于相邻正整数n与n＋1之间，试求n的值。上一题