高中数学必修5：正弦定理(苏教版)课件 46页

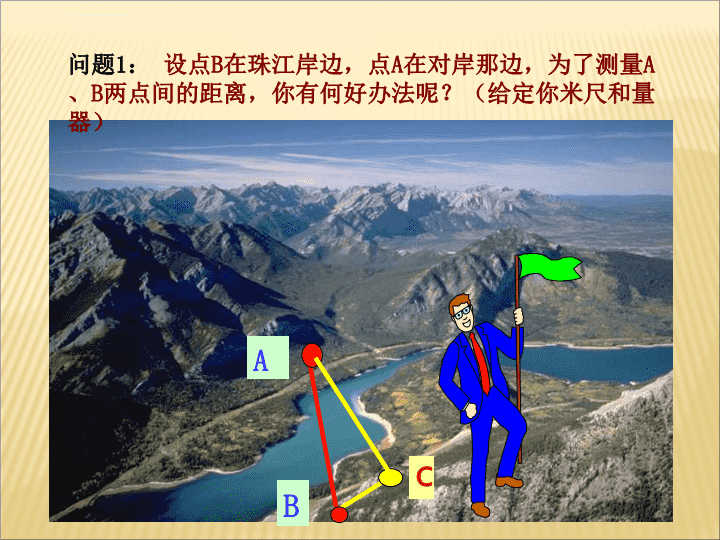
高一数学李凤廷2016.05.231.1正弦定理高中数学必修5\n1.上网活动：“美丽的山河”图片搜索，感受到自然界的美。2.教师导语：自然界神奇美丽，要揭开其神秘的面纱，需要借助于很多数学知识。一、情景导入：\nABC问题1：设点B在珠江岸边，点A在对岸那边，为了测量A、B两点间的距离，你有何好办法呢？（给定你米尺和量器）\nABC设问若将点C移到如下图所示的位置，你还能求出A、B两点间的距离吗？\nCA问题2：此类问题可以归纳为在三角形中，已知某些边与角，求其他的边与角的问题，此类问题在数学里称为___________问题.解三角形B1、测出角B、C的大小2、量出BC的长度\n下面我们回顾一下初中所学的边角关系知识：在Rt△ABC中,各角与其对边的关系:不难得到:CBAabc\n在非直角三角形ABC中有这样的关系吗?（猜想----证明）AcbaCB\n正弦定理:在一个三角形中,各边和它所对角的正弦的比相等.即\n(1)若直角三角形,已证得结论成立.所以AD=csinB=bsinC,即同理可得DAcbCB图1过点A作AD⊥BC于D,此时有证法1:(2)若三角形是锐角三角形,如图1,\n由(1)(2)(3)知，结论成立．且仿(2)可得D(3)若三角形是钝角三角形,且角C是钝角如图2,此时也有交BC延长线于D,过点A作AD⊥BC，CAcbB图2\n以上证明方法体现了一种什么样的数学思维规律？答体现了由特殊到一般的数学思维规律。\nAcbCBDa向量法证法2:利用向量的数量积，产生边的长与内角的三角函数的关系来证明.\n\n＝＝求证:证法3:\n证明：OC/cbaCBA作外接圆O,过B作直径BC/,连AC/,\n证明：∵BACDabc而∴同理∴ha证法4:\n剖析定理、加深理解正弦定理可以解决三角形中哪类问题：①已知两角和一边，求其他角和边.②已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角.\n定理的应用例1在△ABC中，已知c=10,A=45。,C=30。求a,b.解：且∵∴b==已知两角和任意边，求其他两边和一角∵∴a==BACbca\n在△ABC中，已知A=75°，B=45°，c=求a，b.在△ABC中，已知A=30°，B=120°，b=12求a，c.[a=,c=][]练习\n例2已知a=16，b=，A=30°.求角B，C和边c已知两边和其中一边的对角,求其他边和角解：由正弦定理得所以Ｂ＝60°,或Ｂ＝120°当时Ｂ＝60°C=90°C=30°当Ｂ＝120°时B16300ABC16316\n变式:a=30,b=26,A=30°求角B，C和边c300ABC2630解：由正弦定理得所以Ｂ＝25.70,或Ｂ＝1800－25.70=154.30由于154.30+300>1800故B只有一解　（如图）C=124.30,\n变式:a=30,b=26,A=30°求角B，C和边c300ABC2630解：由正弦定理得所以Ｂ＝25.70,C=124.30,∵a>b∴A>B,三角形中大边对大角\n已知两边和其中一边的对角,求其他边和角1.根据下列条件解三角形(1)b=13，a=26，B=30°.[B=90°，C=60°，c=](2)b=40，c=20，C=45°.练习注：三角形中角的正弦值小于１时，角可能有两解无解\n课堂小结（1）三角形常用公式：（2）正弦定理应用范围：①已知两角和任意边，求其他两边和一角②已知两边和其中一边的对角，求另一边的对角。(注意解的情况)正弦定理：＝2R\n已知两边和其中一边的对角,求其他边和角时,三角形什么情况下有一解,二解,无解?课后思考\n谢谢大家\nACabab一解\n正弦定理的综合应用\n\n\nCBAP\n\nACBD\n\n\n\n\n\n实际问题例1、如图，要测底部不能到达的烟囱的高AB，从与烟囱底部在同一水平直线上的C、D两处，测得烟囱的仰角分别是，CD间的距离是12m.已知测角仪器高1.5m,求烟囱的高。图中给出了怎样的一个几何图形？已知什么，求什么？想一想\n实例讲解AA1BCDC1D1分析：如图，因为AB=AA1+A1B，又已知AA1=1.5m,所以只要求出A1B即可。解：答：烟囱的高为29.9m.\nABCDEABCDE\nBEDCBEDCA\n解斜三角形的问题，通常都要根据题意，从实际问题中抽象出一个或几个三角形，然后通过解这些三角形，得出所要求的量，从而得到实际问题的解。在这个过程中，贯穿了数学建模的思想。这种思想即是从实际问题出发，经过抽象概括，把它转化为具体问题中的数学模型，然后通过推理演算，得出数学模型的解，再还原成实际问题的解。\n本节小结:\n