- 710.00 KB
- 2022-08-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
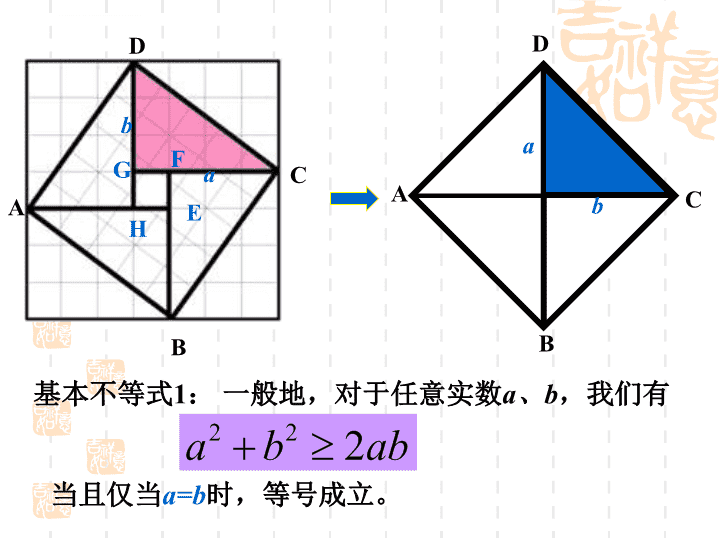
刘海洋§3.4基本不等式:\nICM2002会标赵爽:弦图\nADBCEFGHba基本不等式1:一般地,对于任意实数a、b,我们有当且仅当a=b时,等号成立。ABCDab\n基本不等式2:当且仅当a=b时,等号成立。(2)称为正数a、b的几何平均数称为它们的算术平均数。(1)两个不等式的适用范围不同,而等号成立的条件相同注意:\n基本不等式的几何解释:半弦CD不大于半径ABEDCab\n例1.(1)已知并指出等号成立的条件.(2)已知与2的大小关系,并说明理由.(3)已知能得到什么结论?请说明理由.应用一:利用基本不等式判断代数式的大小关系\n其中恒成立的。(1)(2)(3)(4)练习1:设a>0,b>0,给出下列不等式当且仅当a=b时,等号成立。\n例2、(1)用篱笆围一个面积为100m2的矩形菜园,问这个矩形的长、宽各为多少时,所用篱笆最短。最短篱笆是多少?(2)一段长为36m的篱笆围成一矩形菜园,问这个矩形的长、宽各为多少时,菜园的面积最大。最大面积是多少?\n应用二:解决最大(小)值问题例3、已知都是正数,求证(1)如果积是定值P,那么当时,和有最小值(2)如果和是定值S,那么当时,积有最大值(1)一正:各项均为正数(2)二定:两个正数积为定值,和有最小值。两个正数和为定值,积有最大值。(3)三相等:求最值时一定要考虑不等式是否能取“=”,否则会出现错误小结:利用求最值时要注意下面三条:\n例4、某工厂要建造一个长方形无盖贮水池,其容积为4800立方米,深为3米,如果池底每平方米的造价为150元,池壁每平方米的造价为120元,(1)怎样设计水池能使总造价最低?最低总造价是多少?(2)若受条件限制,水池的长不能超25米,怎样设计水池能使总造价最低?最低总造价是多少?\n变式一:变式二:构造积为定值,利用基本不等式求最值\n构造和为定值,利用基本不等式求最值变式:\n基本不等式的应用应用三:证明不等式\n2、(04重庆)已知则xy的最大值是。练习:1、当x>0时,的最小值为,此时x=。213、若实数,且,则的最小值是()A、10B、C、D、4、在下列函数中,最小值为2的是()A、B、C、D、DC\n构造和为定值,利用基本不等式求最值例5、已知,求的最大值练习:已知且,则最大值是多少?\n例4、求函数的最小值构造积为定值,利用基本不等式求最值\n\n5.若,则()B当且仅当a=b时,等号成立。思考:求函数的最小值