高中数学必修一：23幂函数课件 21页

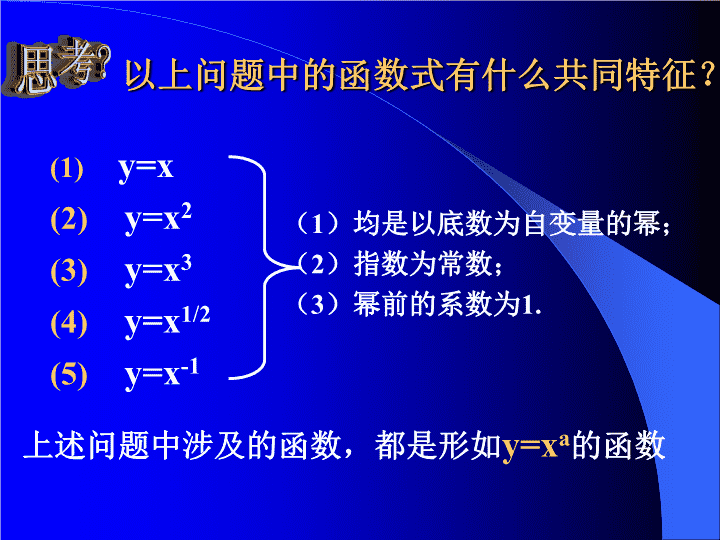
\n1.如果张红购买了每千克1元的苹果w千克，那么她需要付的钱数P=______,______________。2.如果正方形的边长为a，那么正方形的面积是S=，。3.如果立方体的边长为a，那么立方体的体积是V=，。4.如果正方形场地的面积为S，那么正方形的边长a=，。5.如果某人ts内骑车行进了1km，那么他骑车的平均速度v=___________,______________。w这里p是w的函数a²这里S是a的函数a³这里V是a的函数S这里a是S的函数这里v是t的函数tkm/s若将它们的自变量全部用x来表示,函数值用y来表示,则它们的函数关系式将是:问题引入：函数的生活实例\n以上问题中的函数式有什么共同特征？（1）均是以底数为自变量的幂；（2）指数为常数；（3）幂前的系数为1.上述问题中涉及的函数，都是形如y=xa的函数y=xy=x2y=x3y=x1/2y=x-1\n2.3幂函数\n一般地，函数y=xa叫做幂函数，其中x为自变量，a为常数。探究一：幂函数和指数函数有什么不同？\n式子名称常数xy指数函数:y=ax幂函数:y=xαa为底数指数α为指数底数幂值幂值判断一个函数是幂函数还是指数函数切入点看未知数x是指数还是底数幂函数和指数函数的区别指数函数幂函数\n练习1：判断下列函数是否为幂函数(1)y=x4(3)y=-x2(5)y=2x2(6)y=x3+2\n函数图象的画法是：列表、描点、连线初中我们已学习了函数的图象探究2：如何画它们的图象呢？没有学过：\nx…-2-101234…y=x3……y=x1/2……-8-101827010xy1234-1-2-32468-2-4-6-8y=x3//64y=x2\n定义域：值域：奇偶性：单调性：\n定义域：值域：奇偶性：单调性：\n\n(-∞,0)减(-∞,0]减(1,1)公共点(0,+∞)减在[0,+∞)上增函数在R上是增函数[0,+∞)增在R上是增函数单调性奇非奇非偶奇偶奇奇偶性[0,+∞)R[0,+∞)R值域[0,+∞)ＲＲＲ定义域y=x-1y=x3y=x2y=x函数性质幂函数的性质\n在同一平面直角坐标系内作出幂函数y=x，y=x2，y=x3，y=x1/2，y=x-1的图象.几何画板演示\n(1)幂函数的图象都通(3)如果α＞０，在区间[0,+∞)上是当α为偶数，幂函数为幂函数的性质增函数减函数(2)当α为奇数，幂函数为奇函数偶函数(1,1)如果α<０，在区间[0,+∞)上是在第一象限，图象向上与y轴无限接近，向右与x轴无限接近\n例１　比较下列各组数的大小；利用幂函数的单调性比较幂值大小注意:利用两个数中间数,间接比较幂值的大小\n练习2：利用幂函数的性质，比较下列各题中两个幂的值的大小：（1），；（2），；（3），；（4），.\n例2证明幂函数f(x)=x1/2在［0，+∞）上是增函数.\n小结(1)幂函数的定义；(2)幂函数的性质；(3)利用幂函数的单调性判别大小.一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数.\n分层作业1.课本p.7922.作出函数的图象，根据图象讨论这个函数有哪些性质，并给出证明．3.课外思考：用图象法确定方程解的个数.（1）；（2）\n谢谢！