- 1.44 MB
- 2022-08-10 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
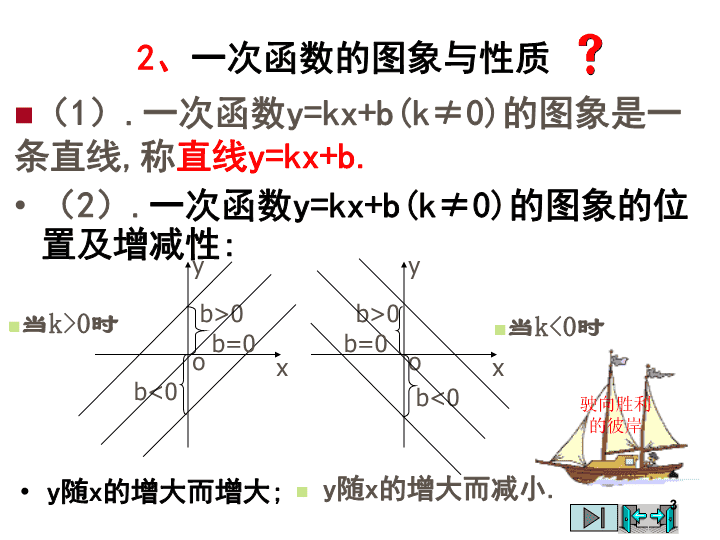
函数1\n一、一次函数1.若两个变量x,y的关系可以表示成y=kx+b(k,b是常数,k≠0)的形式,则称y是x的一次函数(x为自变量,y为因变量).2.特别地,当常数b=0时,一次函数y=kx+b(k≠0)就成为:y=kx(k是常数,k≠0),称y是x的正比例函数.3.一次函数与正比例函数之间的关系:正比例函数是当b=0时的特殊的一次函数.2\n2、一次函数的图象与性质(2).一次函数y=kx+b(k≠0)的图象的位置及增减性:y随x的增大而增大;(1).一次函数y=kx+b(k≠0)的图象是一条直线,称直线y=kx+b.驶向胜利的彼岸xyoxyoy随x的增大而减小.b<0b>0b=0b<0b>0b=0当k>0时当k<0时3\n作出下列一次函数的图象(1)(2)(3)4\n3、反比例函数的图象及性质(1)形状反比例函数的图象是由两支双曲线组成的.因此称反比例函数的图象为双曲线;(2)位置当k>0时,两支双曲线分别位于第一,三象限内;当k<0时,两支双曲线分别位于第二,四象限内;驶向胜利的彼岸xyoxyo5\n(3).增减性反比例函数的图象,当k>0时,在每一象限内,y随x的增大而减小;当k<0时,在每一象限内,y随x的增大而增大.(4).图象的发展趋势反比例函数的图象无限接近于x,y轴,但永远达不到x,y轴,画图象时,要体现出这个特点.(5).对称性反比例函数的图象是关于原点成中心对称的图形.驶向胜利的彼岸xyoxyo6\n画出下列反比例函数图象1.2.3.4.7\n四、二次函数1.定义:一般地,形如y=ax²+bx+c(a,b,c是常数,a≠0)的函数叫做x的二次函数.2.定义要点:(1)关于x的代数式一定是整式,a,b,c为常数,且a≠0.(2)等式的右边最高次数为2,可以没有一次项和常数项,但不能没有二次项.3.几种不同表示形式:驶向胜利的彼岸8\n4、二次函数y=ax²+bx+c(a≠0)的图像和性质今后解决二次函数问题时,要善于借助函数图像,利用数形结合的思想方法解决问题.抛物线顶点坐标对称轴位置开口方向增减性最值y=ax2+bx+c(a>0)y=ax2+bx+c(a<0)由a,b和c的符号确定由a,b和c的符号确定向上向下在对称轴的左侧,y随着x的增大而减小.在对称轴的右侧,y随着x的增大而增大.在对称轴的左侧,y随着x的增大而增大.在对称轴的右侧,y随着x的增大而减小.根据图形填表:9\n5、二次函数与一元二次方程二次函数y=ax2+bx+c的图象和x轴交点的坐标与一元二次方程ax2+bx+c=0的根有什么关系?二次函数y=ax2+bx+c的图象和x轴交点一元二次方程ax2+bx+c=0的根一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac有两个交点有两个相异的实数根b2-4ac>0有一个交点有两个相等的实数根b2-4ac=0没有交点没有实数根b2-4ac<010\n11\n12\n13\n4-1例8:当时,求函数y=2x2-8x+1的最小值、最大值。2Oxy-7分析:由图象知,当x=2时,y有最小值,ymin=f(2)=-7,当x=-1时,y有最大值,y=f(-1)=11,max\n15\n2、二次函数 图象的顶点坐标和对称轴方程为( )A、(1,-2),x=1B、(1,2),x=1C、(-1,-2),x=-1D、(-1,2),x=-1DA1、抛物线 的对称轴及顶点坐标分别是( )A、y轴,(0,-4) B、x=3,(0,4)C、x轴,(0,0) D、y轴, (0,3)练习:16\n3、函数 的开口方向,顶点坐标是,对称轴是.当x时.y随x的增大而减小。当x时.y有最为.向上<-1=-1小数形结合顶点坐标公式17\n因此:所求二次函数是:y=2x2-3x+54.已知一个二次函数的图象过点(-1,10),(1,4),(2,7)三点,求这个函数的解析式?解:设所求的二次函数为y=ax2+bx+c由条件得:a-b+c=10a+b+c=44a+2b+c=7解得a=2,b=-3,c=55.已知二次函数y=ax2+bx+c的最大值是2,图象顶点在直线y=x+1上,并且图象经过点(3,-6).求a、b、c解:∵二次函数的最大值是2∴抛物线的顶点纵坐标为2又∵抛物线的顶点在直线y=x+1上∴当y=2时,x=1∴顶点坐标为(1,2)∴设二次函数的解析式为y=a(x-1)2+2又∵图象经过点(3,-6)∴-6=a(3-1)2+2∴a=-2∴二次函数的解析式为y=-2(x-1)2+2即:y=-2x2+4x.18\n19\n此课件下载可自行编辑修改,供参考!感谢您的支持,我们努力做得更好!