高中数学《正弦定理》公开课优秀课件 21页

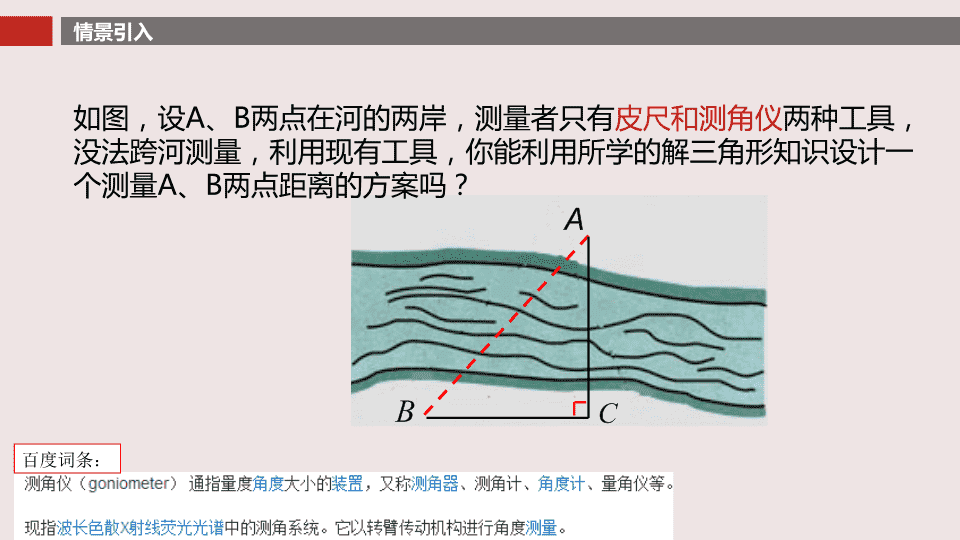
全国高中青年数学教师优质课评比《正弦定理》第一课\n《正弦定理》第一课学习目标通过观察、实验、验证、猜想、证明，从特殊到一般得到正弦定理；能证明正弦定理，了解正弦定理的一些推导方法；初步熟知正弦定理的两个重要应用。\n情景引入如图，设A、B两点在河的两岸，测量者只有皮尺和测角仪两种工具，没法跨河测量，利用现有工具，你能利用所学的解三角形知识设计一个测量A、B两点距离的方案吗？百度词条：\n情景引入如图，设两点在河的两岸，测量者为了得到两点之间的距离.测量者在的同侧河岸选定一个点,测出的距离是.，根据这些数据能解决这个问题吗？\n数学建模任意三角形中，有大角对大边，小角对小边的边角关系。D\n探究1直角三角形边角数量关系\n探究2斜三角形边角数量关系实验1实验2实验3\n猜想对于任意的斜三角形也存在以下边角数量关系：探究2斜三角形边角数量关系\n证明1探究2斜三角形边角数量关系钝角三角形呢？D\n正弦定理（lawofsines）在任意一个三角形中，各边和它所对的角的正弦的比相等.即概念生成，突出核心是否可以用其他的方法证明正弦定理?\n其他证明方法介绍证明2D\n定义：一般地，把三角形的三个角A、B、C和它们的对边a、b、c叫做三角形的元素，已知三角形的几个元素求其他的元素的过程叫做解三角形。定理应用，解决引例\n学以致用\n定理应用总结已知三角形的任意两个角与一边，解三角形.正弦定理（lawofsines）\n学以致用\n定理应用总结已知三角形的任意两边与其中一边的对角，解三角形.正弦定理（lawofsines）\n1、定理应用归纳已知三角形的任意两个角与一边，解三角形。正弦定理（lawofsines）如：2、已知三角形任意两边与其中一边的对角，解三角形。如：还有其它情况吗？\n2、正弦定理的主要应用：已知三角形的两角及一边，解三角形；已知三角形的两边和其中一边的对角，解三角形；3、转化划归思想、分类讨论的思想、方程思想等.课堂小结，总结回顾\n1、探索整理正弦定理的其他证明方法；2、通过以下题目，在“已知三角形两条边和其中一边的对角”的条件下进一步探究正弦定理的应用：课后作业\n谢谢观看\n谢谢！