【高中数学课件】一元二次不等式ppt课件 18页

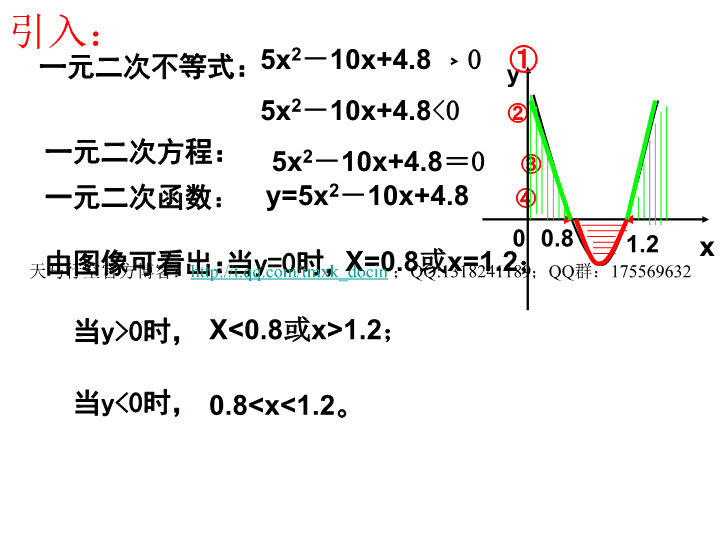
一元二次不等式天马行空官方博客：http://t.qq.com/tmxk_docin；QQ:1318241189；QQ群：175569632\n考试大纲(1)会从实际情景中抽象出一元二次不等式模型.(2)通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.(3)会解一元二次不等式,给定的一元二次不等式,会设计求解的程序框图.天马行空官方博客：http://t.qq.com/tmxk_docin；QQ:1318241189；QQ群：175569632\n引入：5x2－10x+4.8<0②一元二次不等式：一元二次方程：5x2－10x+4.8＝0③y=5x2－10x+4.8④0.81.2xy0由图像可看出：当y=0时，X=0.8或x=1.2；当y>0时，X<0.8或x>1.2；0.80;(2)-x2-2x+3≥0;(3)x2-2x+1<0;(4)x2-2x+2<0.反思：求解一元二次不等式首先要看对应一元二次方程根的情况！\n求解一元二次不等式首先要看对应一元二次方程根的情况！你能简述求解不等式ax2+bx+c<0(a>0)的步骤吗？流程图吗输入a,b,c△＝b2-4ac△>0N输出”解集为ф”Y输出{x|x10解：由题意，得：⊿=25a2－241.当⊿=25a2－24>0，2.当⊿=25a2－24=0，3.当⊿=25a2－24<0,解集为：解集为：解集为：R.二、典型题选讲（含参不等式的解法）\n变式1.x2+5ax+6a2>0解：因式分解，得:（x+3a)(x+2a)>0，方程（x+3a)(x+2a)＝0的两根为－3a、－2a.①当－3a>－2a即a<0时，解集为：{x︱x>－3a或x<－2a};②当－3a=－2a即a=0时，解集为：{x︱x∈R且x≠0}；③当－3a<－2a即a>0时，综上：当a>0时，解集为：{x︱x>－2a或x<－3a}.当a=0时，解集为：{x︱x∈R且x≠0};当a<0时，解集为：{x︱x>－3a或x<－2a};解集为：{x︱x>－2a或x<－3a}.原不等式为x2>0\n变式2.ax2+(6a+1)x+6>0二、当a≠0时，①当a<0时，一、当a=0时，②当a>0时，⑴⑶⑵∴综上，得\n注：解形如ax2+bx+c>0的不等式时分类讨论的标准有：1、讨论a与0的大小；2、讨论⊿与0的大小；3、讨论两根的大小；\n例2关于x的二次不等式a2x2+6ax+9－b2≤0的解集是[－1，2]，求a,b解：依题意知方程a2x2+6ax+9—b2=0的两根为—1,2∴\n（1）二次不等式ax2+bx+c>0恒成立例题：已知关于x的不等式：(a-2)x2+(a-2)x+1≥0恒成立，解：由题意知：①当a-2=0，即a=2时，不等式化为②当a-2≠0，即a≠2时，原题等价于综上：试求a的取值范围.1≥0，它恒成立，满足条件.知识概要（2）二次不等式ax2+bx+c<0恒成立（3）二次不等式ax2+bx+c≥0恒成立（4）二次不等式ax2+bx+c≤0恒成立(二)含参不等式恒成立的问题借助图象\n例2：解关于x的不等式x2-(a+1)x+a>0变形1：解关于x的不等式x2-ax-(a+1)>0(a≠0)引申1：解关于x的不等式ax2-(a+1)x+1>0(a≠0)分类讨论！\n变形2：求函数的定义域。引申2：若的定义域为R,求b范围。拓展：若的值域为R,求b范围。\n作业与思考R-12-2-2≤a≤6思考题：作业：73页第1、2题