高中数学优质课教学设计及课件算法案例作课课件 14页

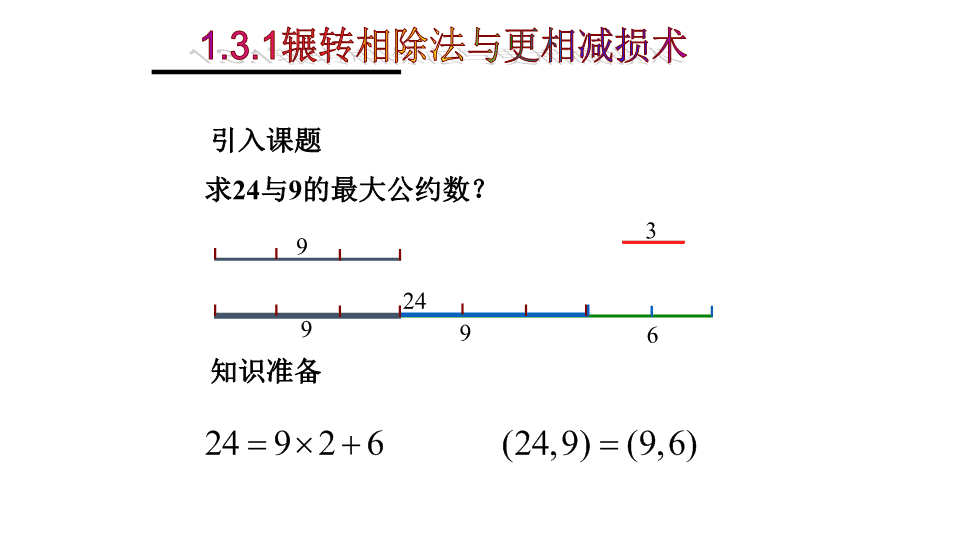
1.3算法案例辗转相除法与更相减损术郑州一中胡莉萍人教版（数学）必修三\n引入课题求24与9的最大公约数？知识准备1.3.1辗转相除法与更相减损术2493996\n1.3.1辗转相除法与更相减损术(一）自主学习请同学们结合课本的基础知识，思考解决《学习指导书》第1-2页问题。\n1.3.1辗转相除法与更相减损术(二）交流研讨请同学们讨论各自的疑惑及感悟，提出问题，并相互解决。\n1.关于辗转相除法的算理问题所以1.3.1辗转相除法与更相减损术(三）精讲\n1.关于辗转相除法的算理问题1.3.1辗转相除法与更相减损术(三）精讲以上满足：\n第二步，计算m除以n所得的余数r.第三步，m=n，n=r.第四步，若r=0，则m，n的最大公约数等于m；否则，返回第二步.第一步，给定两个正整数m，n.2.设计算法之算法步骤1.3.1辗转相除法与更相减损术(三）精讲\n（1）确立循环体:求m除以n的余数r,m=n,n=r（2）初始化变量：输入m,n（3）设定循环控制条件：r=0？2.设计算法之构造循环结构1.3.1辗转相除法与更相减损术(三）精讲\n求m除以n的余数r开始输入m，nm=nn=rr=0？是输出m结束否1.3.1辗转相除法与更相减损术\n例1用更相减损术求98与63的最大公约数.解：由于63不是偶数，把98和63以大数减小数，并辗转相减，如图所示：98－63＝3563－35＝2835－28＝728－7＝2121－7＝1414－7＝7所以，98与63的最大公约数是7．3.更相减损术\n名称辗转相除法更相减损术区别联系小结辗转相除法与更相减损术的比较:（1）以除法为主.（2）两个整数差值较大时运算次数较少.（3）相除余数为零时得结果.（1）以减法为主.（2）两个整数差值较大时运算次数较多.（3）相减，两数相等得结果，相减前要做是否都是偶数的判断.（1）都是求最大公约数的方法.（2）二者的实质都是递推的过程.（3）二者都要用循环结构来实现.\n开始i=m+1输入：m,nmMODi=0且nMODi=0?i=i-1输出：i结束是否m>n?t=m,m=n,n=t否是穷举法程序框图1.3.1辗转相除法与更相减损术\n两个正整数的最小公倍数的算法最小公倍数＝求m除以n的余数r开始输入m，nm=nn≠0？否输出是n=r1.3.1辗转相除法与更相减损术\n1.必做题：用辗转相除法求下列两数的最大公约数，并用更相减损术检验你的结果：（1）228，48；（2）185，98.2.选做题：求225，135最小公倍数．3.拓展延伸：请查阅相关书籍资料画出更相减损术这种算法的程序框图，并用语句来描述这个算法．1.3.1辗转相除法与更相减损术(四）自我测评