高中数学：正弦定理课件人教新课标必修5 21页

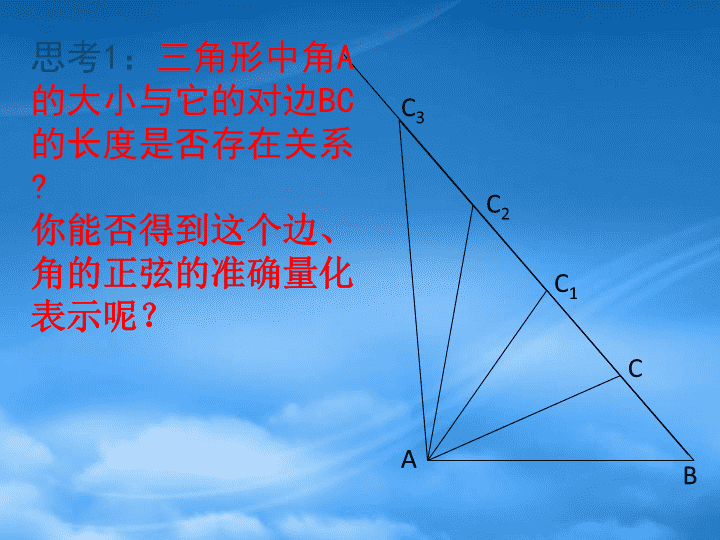
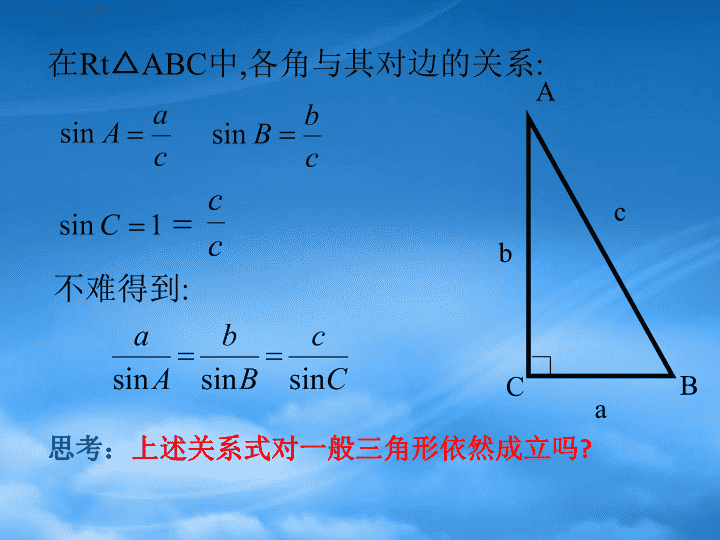
正弦定理\nABC3C2C1C思考1：三角形中角A的大小与它的对边BC的长度是否存在关系?你能否得到这个边、角的正弦的准确量化表示呢？\n在Rt△ABC中,各角与其对边的关系:不难得到:CBAabc思考：上述关系式对一般三角形依然成立吗?\n所以CD=asinB=bsinA,即同理可得DCabAB图1过点C作CD⊥AB于D,此时有若三角形是锐角三角形,如图1,探究一\n且仿上可得D若三角形是钝角三角形,以上等式仍然成立吗?此时也有交BC延长线于D,过点A作AD⊥BC，CAcbB图2探究二\n思考2：是否可以用向量方法证明正弦定理?BcaCADb利用向量的数量积，产生边的长与内角的三角函数的关系来证明.j\n证明：过A作单位向量垂直于∴asinC=csinA.同理，过点C作与垂直的单位向量，可得BCA则两边同乘以单位向量\n正弦定理:在一个三角形中,各边和它所对角的正弦的比相等.即?思考:这个比值会是什么呢?\n探究：OC/cbaCBA作外接圆O,过B作直径BC/,连AC/,\n剖析定理、加深理解②已知两角和一边，求其他角和边.①已知两边和其中一边的对角，求另一边的对角，进而可求其他的边和角.思考：利用正弦定理可以解决哪些问题？正弦定理解三角形：已知三角形的几个元素求其他元素的过程\n例题讲解已知两角和任意边，求其他两边和一角解：\n例题讲解已知两边和其中一边的对角,求其他边和角解：\n变式一：在△ABC中，已知a=20cm，b=cm，A=600，解三角形（角度精确到10,边长精确到1cm）.\n变式二：\n一般地，已知两边和其中一边的对角解三角形，有两解、一解、无解三种情况.已知a，b，A，解三角形（大边对大角）\n已知a，b，A，解三角形当A为钝角或直角时：AABCBC无解有一解\n已知a，b，A，解三角形当A为锐角时：ABC只有一解无解一解两解\n思考：如果已知a，b及角A，如何表示三角形的面积?ABCacbD\n练习：在△ABC中，A=60°,b=1,面积为\n课堂小结（1）三角形常用公式：（2）正弦定理应用范围：①已知两角和任意边，求其他两边和一角②已知两边和其中一边的对角，求另一边的对角。(注意解的情况)正弦定理：＝2R\n