函数单调性课件-ppt-高中数学-精品 26页

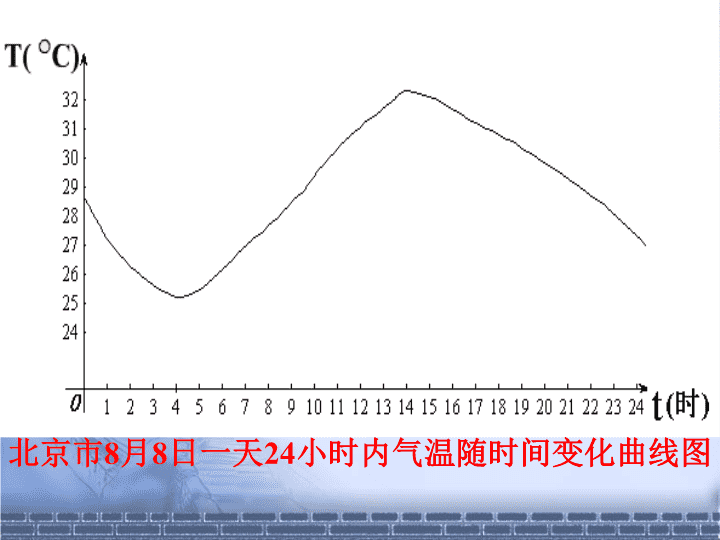
函数的单调性\n数与形,本是相倚依焉能分作两边飞数无形时少直觉形少数时难入微数形结合百般好隔离分家万事休切莫忘,几何代数统一体永远联系莫分离——华罗庚\n北京市8月8日一天24小时内气温随时间变化曲线图\n广元市年生产总值统计表年份生产总值（亿元）\n苍溪县日平均出生人数统计表年份人数（人）\n能用图象上动点P（x，y）的横、纵坐标关系来说明上升或下降趋势吗？xyoxyoxyo在某一区间内，当x的值增大时,函数值y也增大——图像在该区间内逐渐上升；当x的值增大时,函数值y反而减小——图像在该区间内逐渐下降。函数的这种性质称为函数的单调性局部上升或下降下降上升\ny246810O-2x84121620246210141822I\n对区间I内x1，x2，当x1单调区间\n（2）函数单调性是针对某个区间而言的，是一个局部性质;（1）如果函数y=f(x)在区间I是单调增函数或单调减函数，那么就说函数y=f(x)在区间I上具有单调性。在单调区间上，增函数的图象是上升的，减函数的图象是下降的。注意：判断1：函数f(x)=x2在是单调增函数；xyo\n（2）函数单调性是针对某个区间而言的，是一个局部性质;（1）如果函数y=f(x)在区间I是单调增函数或单调减函数，那么就说函数y=f(x)在区间I上具有单调性。在单调区间上，增函数的图象是上升的，减函数的图象是下降的。注意：判断2：定义在R上的函数f(x)满足f(2)>f(1)，则函数f(x)在R上是增函数；（3）x1,x2取值的任意性yxO12f(1)f(2)\n下表是函数中y随x的变化情况x…-4-3-2-101234……16941014916…分析函数值的变化可得到函数的单调性。\n例1.画出下列函数图像，并写出单调区间：数缺形时少直观xy_____________,讨论1：根据函数单调性的定义，2试讨论　　　　　　　在　　　和　　　上的单调性？？\n单调区间的书写：函数在其定义域内某一点处的函数值是确定的，讨论函数在某点处的单调性无意义。若函数在区间端点处有定义，则写成闭区间，当然写成开区间也可以，若函数在区间端点处无定于，则必须写成开区间。\n变式2：讨论的单调性成果交流变式1：讨论的单调性xyy=-x2+21-1122-1-2-2_______;_______.例2.画出下列函数图像，并写出单调区间：\n单调增区间单调减区间a>0a<0的对称轴为返回\n成果运用若二次函数在区间上单调递增，求a的取值范围。\n成果运用若二次函数在区间上单调递增，求a的取值范围。解：二次函数的对称轴为,由图象可知只要，即即可.oxy1xy1o\n例3.判断函数在定义域上的单调性.1.任取x1，x2∈D，且x1