高中数学_直线与圆的位置关系课件 15页

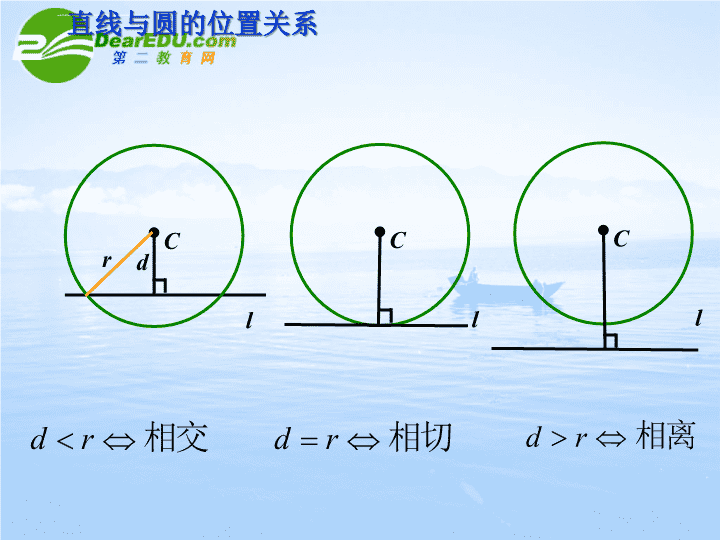
2.3直线与圆的位置关系\n想一想，平面几何中，直线与圆有哪几种位置关系？在初中，我们怎样判断直线与圆的位置关系？平面几何中，直线与圆有三种位置关系：（1）直线和圆有两个公共点，直线与圆相交；（1）（2）直线和圆只有一个公共点，直线与圆相切；（2）（3）直线和圆没有公共点，直线与圆相离．（3）问题引入\nCldrClCl直线与圆的位置关系\n问题的引入2、现在，如何用直线方程和圆的方程判断它们之间的位置关系？先看以下问题，看看你能否从问题中总结来．\n已知直线与圆，判断它们的位置关系。已知圆的圆心是O(0,0),半径是r=1,圆心到直线的距离所以，此直线与圆相切xyop构建新知\n已知直线与圆，判断它们的位置关系。建立方程组②①由①可知，代入②中得，化简得，方程组有唯一一个解即此直线与圆只有一个公共点，从而直线与圆相切构建新知\n判断直线与圆的位置关系有两种方法：代数法：根据直线与圆的方程组成的方程组解的情况来判断．如果有两组实数解时，直线与圆相交；有一组实数解时，直线与圆相切；无实数解时，直线与圆相离．几何法：根据圆心到直线的距离d与圆的半径r的关系来判断．如果dr，直线与圆相离．回顾我们前面提出的问题：如何用直线和圆的方程判断它们之间的位置关系？构建新知\n解法一：圆可化为其圆心C的坐标为（0，1），半径长为，点C（0，1）到直线l的距离所以，直线l与圆相交．分析：依据圆心到直线的距离与半径长的关系，判断直线与圆的位置关系（几何法）；例1、如图，已知直线l：和圆心为C的圆，判断直线l与圆的位置关系；\n解法二：所以，直线与圆有两个交点，直线l与圆相交。分析:根据直线与圆的方程组成的方程组解的情况来判断（代数法）①②代入②，由①可得消去y,得\n例2设直线和圆相切，求实数m的值。解法一：已知圆的圆心为O(0,0),半径r=1,则O到已知直线的距离由已知得d=r,即解得m=O(0,2)xy\nO2xy解法二：把直线方程与圆的方程联立得把①代入②中得由直线和圆相切可得：\n(1)证明：无论a为何实数，直线l与圆C恒相交(2)试求直线l被圆C截得弦长的最大值C(2,4)xyAB0dD\n另解：（1）因为l：y=a(x-1)+4过定点N（1，4）N与圆心C（2，4）相距为1显然N在圆C内部，故直线l与圆C恒相交（2）在y=ax+4-a中,a为斜率，当a=0时，l过圆心，弦AB的最大值为直径的长，等于6C(2,4)xyAB0N\n练习：1、判断直线与圆的位置关系。2、以C(1,3)为圆心，为半径的圆与直线相切，求实数m的值\n把直线方程代入圆的方程得到一元二次方程求出△的值确定圆的圆心坐标和半径r计算圆心到直线的距离d判断d与圆半径r的大小关系归纳小节直线和圆的位置关系的判断方法几何方法代数方法