高中数学_任意角与弧度制_教学课件 16页

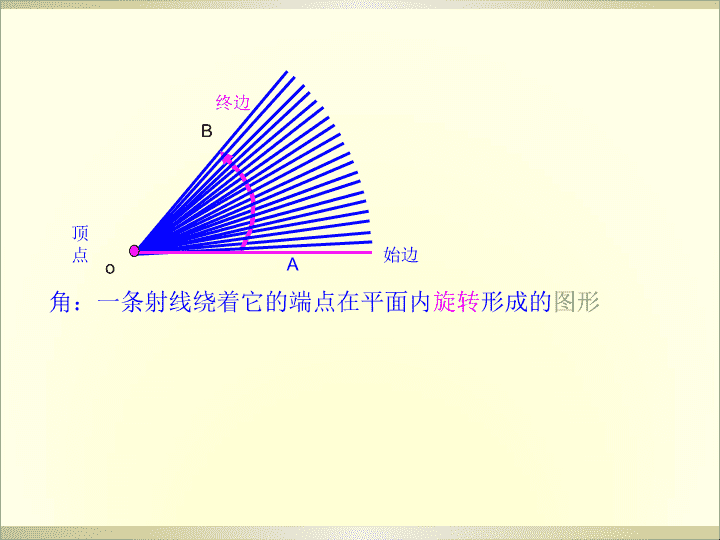
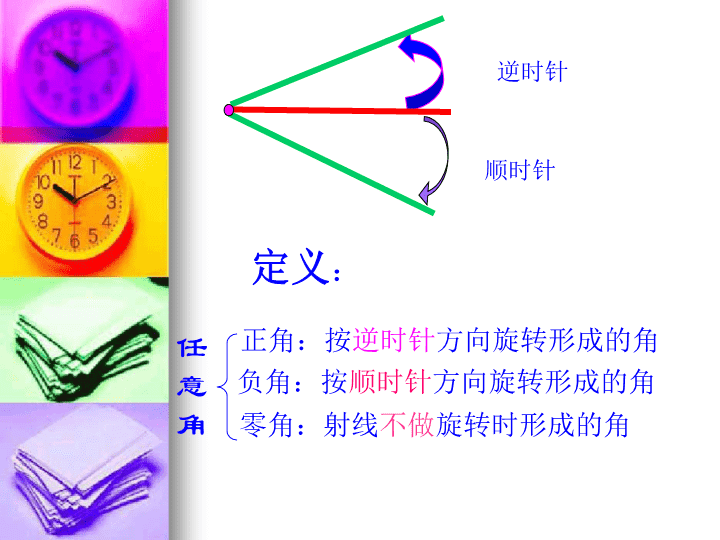
§1.1.1角的概念的推广\noAB始边终边顶点角：一条射线绕着它的端点在平面内旋转形成的图形\n逆时针顺时针定义：正角：按逆时针方向旋转形成的角负角：按顺时针方向旋转形成的角零角：射线不做旋转时形成的角任意角\n为了研究方便，我们往往在平面直角坐标系中来讨论角。象限角:(1)角的顶点与坐标原点重合(2)始边与X轴的非负半轴重合终边落在第几象限就称角是第几象限角oxy轴线角:终边落在坐标轴上就称角是轴限角\n请在同一坐标系上画出30°,390°,-330°,并找出它们的共同点?xyo3003900-3300\n注:（1）K∈Z（2）是任意角（3）相等的角终边一定相同，但终边相同的角不一定相等，终边相同的角有无数多个，它们相差360°的整数倍S={β|β=α+k·3600,K∈Z}与角终边相同的角的表示：\n例1在0º到360º范围内，找出与下列各角终边相同的角，并判断它是哪个象限的角.(1)－120º；(2)640º；(3)-950º12′.⑶∵－950º12'=129º48'－3×360º，∴129º48'的角与－950º12'的角终边相同，它是第三象限角．解：⑴∵－120º=240º－360º，∴240º的角与－120º的角终边相同，它是第三象限角．⑵∵640º=280º+360º，∴280º的角与640º的角终边相同，它是第四象限角．\n【变式训练1】-330°是第象限角;1065°是第象限角.解析:∵-330°=-360°+30°,30°是第一象限角,∴-330°是第一象限角.∵1065°=2×360°+345°,345°是第四象限角,∴1065°是第四象限角.答案:一四\n例2写出与下列各角终边相同的角的集合S，并把S中在－360º~720º间的角写出来：(1)60º；(2)－21º；(3)363º14′解：(1)S={β|β=60º+k·360º，k∈Z}S中在－360º～720º间的角是60º－1×360º=－300º；60º+0×360º=60º；60º+1×360º=420º\n(2)S={β|β=－21º+k·360º，k∈Z}S中在－360º～720º间的角是－21º+0×360º=－21º；－21º+1×360º=339º；－21º+2×360º=699º．(3)S={β|β=363º14‘+k·360º，k∈Z}S中在－360º～720º间的角是363º14'－2×360º=－356º46'；363º14'－1×360º=3º14'；363º14'+0×360º=363º14'．\n\n\n【例3】如图.(1)分别写出终边落在OA,OB位置上的角的集合;(2)写出终边落在阴影部分(包括边界)的角的集合.分析:(1)根据图示,首先确定终边满足条件的一个角α,再利用终边相同的角的集合进行表示.(2)首先确定终边落在阴影部分的边界位置的角,再用不等式表示阴影部分的角,最后组成集合.解:(1)终边落在OA位置上的角的集合为{α|α=90°+45°+k·360°,k∈Z}={α|α=135°+k·360°,k∈Z},终边落在OB位置上的角的集合为{β|β=-30°+k·360°,k∈Z}.(2)由题图可知,阴影部分角的集合可表示为{α|-30°+k·360°≤α≤135°+k·360°,k∈Z}.\n\n小结：1.任意角的概念正角：射线按逆时针方向旋转形成的角负角：射线按顺时针方向旋转形成的角零角：射线不作旋转形成的角1)置角的顶点于原点2)始边重合于X轴的非负半轴2.象限角3)终边落在第几象限就是第几象限角3.终边与角α相同的角α＋K·360°，K∈Z轴线角:终边落在坐标轴上就称角是轴限角\n知识回顾KnowledgeReview祝您成功！