高中数学函数的奇偶性ppt课件 22页

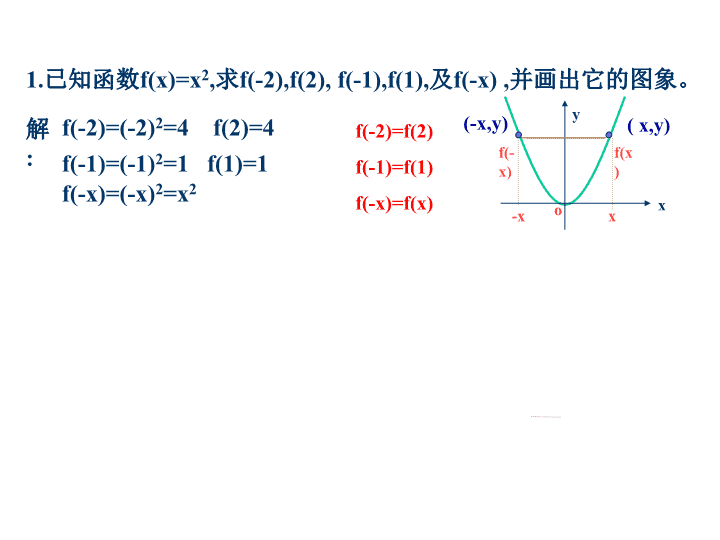
1.3.2函数的奇偶性\n1.已知函数f(x)=x2,求f(-2),f(2),f(-1),f(1),及f(-x),并画出它的图象。解:f(-2)=(-2)2=4f(2)=4f(-1)=(-1)2=1f(1)=1f(-x)=(-x)2=x2f(-2)=f(2)f(-1)=f(1)f(-x)=f(x)-xxf(-x)f(x)xyo(x,y)(-x,y)\n1.偶函数的概念:偶函数定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=f(x),那么函数f(x)就叫偶函数.\n2.已知f(x)=x3,画出它的图象,并求出f(-2),f(2),f(-1),f(1)及f(-x)解:f(-2)=(-2)3=-8f(2)=8f(-1)=(-1)3=-1f(1)=1f(-x)=(-x)3=-x3f(-2)=-f(2)f(-1)=-f(1)f(-x)=-f(x)-xf(-x)xf(x)xyo(-x,-y)(x,y)\n1.奇函数的概念:奇函数定义:如果对于f(x)定义域内的任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫奇函数.\n☆奇函数、偶函数定义的说明:(1).函数具有奇偶性的前提：定义域关于原点对称。[a,b][-b,-a]xo（2）.奇、偶函数定义的逆命题也成立，即：若f(x)为奇函数,则f(-x)=－f(x)成立。若f(x)为偶函数,则f(-x)=f(x)成立。（3）如果一个函数f(x)是奇函数或偶函数,那么我们就说函数f(x)具有奇偶性。\n练习1.说出下列函数的奇偶性:偶函数奇函数奇函数奇函数①f(x)=x4________④f(x)=x-1__________②f(x)=x________奇函数⑤f(x)=x-2__________偶函数③f(x)=x5__________⑥f(x)=x-3_______________说明：对于形如f(x)=xn的函数，若n为偶数，则它为偶函数。若n为奇数，则它为奇函数。\n例1.判断下列函数的奇偶性(1)f(x)=x3+2x(2)f(x)=2x4+3x2解:∵f(-x)=(-x)3+2(-x)=-x3-2x=-(x3+2x)即f(-x)=-f(x)∴f(x)为奇函数∵f(-x)=2(-x)4+3(-x)2=2x4+3x2∴f(x)为偶函数定义域为R解:定义域为R即f(-x)=f(x)\n⑴先求定义域，看是否关于原点对称;⑵再判断f(－x)=-f(x)或f(-x)=f(x)是否恒成立。用定义判断函数奇偶性的步骤:\n练习2.判断下列函数的奇偶性(2)f(x)=-x2+1∴f(x)为奇函数∵f(-x)=-(-x)2+1=-x2+1∴f(x)为偶函数(1)f(x)=x-1x解：定义域为﹛x|x≠0﹜解：定义域为R∵f(-x)=(-x)-1-x=-x+1x即f(-x)=-f(x)即f(-x)=f(x)\n(3).f(x)=5(4)f(x)=0解:(3)f(x)的定义域为R∵f(-x)=f(x)=5∴f(x)为偶函数解:(4)定义域为R∵f(-x)=f(x)=0又f(-x)=-f(x)=0∴f(x)为既奇又偶函数yox5oyx说明:函数f(x)=0(定义域关于原点对称），为既奇又偶函数。\n(5).f(x)=x+1(6).f(x)=x2x∈[-1,3]解:(5)∵f(-x)=-x+1-f(x)=-x-1∴f(-x)≠f(x)且f(-x)≠–f(x)∴f(x)为非奇非偶函数解:（6）∵定义域不关于原点对称∴f(x)为非奇非偶函数yoxox-13y\n奇函数说明：根据奇偶性,偶函数函数可划分为四类:既奇又偶函数非奇非偶函数\nxoy-aa(a,f(a))(-a,f(-a))偶函数的图象关于y轴对称，反过来，如果一个函数的图象关于y轴对称，那么这个函数是偶函数.\nxoy(a,f(a))(-a,f(-a))-aa奇函数的图象关于原点对称，反过来，如果一个函数的图象关于原点对称，那么这个函数是奇函数.\noyx例3已知函数y=f(x)是偶函数，它在y轴右边的图象如图，画出y=f(x)在y轴左边的图象。\n例2.根据下列函数图象,判断函数奇偶性.yxyxyxyxy\n用定义法判断函数奇偶性解题步骤:(1)先确定函数定义域,并判断定义域是否关于原点对称;(2)求f(-x)，找f(x)与f(-x)的关系;若f(-x)=f(x),则f(x)是偶函数;若f(-x)=-f(x),则f(x)是奇函数.(3)作出结论.f(x)是偶函数或奇函数或非奇非偶函数或即是奇函数又是偶函数。\n2.奇偶函数图象的性质:⑴奇函数的图象关于原点对称.反过来,如果一个函数的图象关于原点对称,那么这个函数为奇函数.⑵偶函数的图象关于y轴对称.反过来,如果一个函数的图象关于y轴对称,那么这个函数为偶函数.注：奇、偶函数图象的性质可用于：①.简化函数图象的画法。②.判断函数的奇偶性。\n课堂小结1奇偶性定义:对于函数f(x),在它的定义域内，①若有f(-x)=-f(x),则f(x)叫做奇函数；②若有f(-x)=f(x),则f(x)叫做偶函数。2图象性质:奇函数的图象关于原点对称;偶函数的图象关于y轴对称.3判断奇偶性方法：图象法，定义法。4定义域关于原点对称是函数具有奇偶性的前提\n奇偶函数定义图像性质定义域对称图像法、定义法\n作业：课本P39AT6BT3