1. 您所在位置：首页 > 中小学教育 > 高中教育 > 课件 > 高中数学课件圆与圆的位置关系

高中数学课件圆与圆的位置关系 54页

  • 1.56 MB
  • 2022-08-13 发布

高中数学课件圆与圆的位置关系

  • 54页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
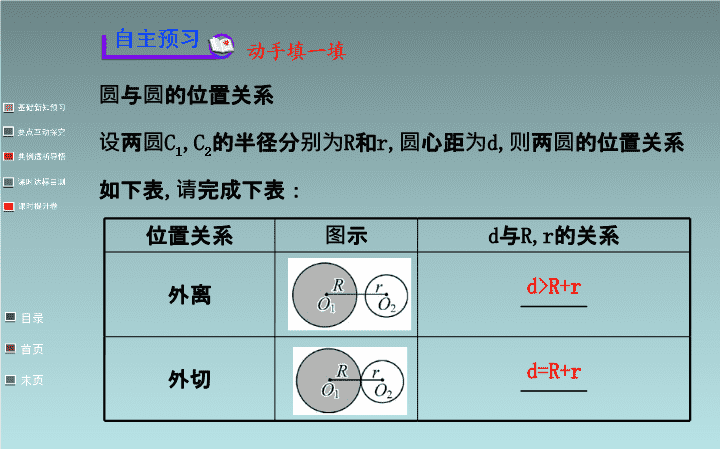
4.2.2圆与圆的位置关系\n1.理解圆与圆的五种位置关系.2.会利用两点间的距离公式求两圆的圆心距.3.会用连心线的长判断两圆的位置关系.\n圆与圆的位置关系设两圆C1,C2的半径分别为R和r,圆心距为d,则两圆的位置关系如下表,请完成下表：位置关系图示d与R,r的关系外离______外切______d>R+rd=R+r\n位置关系图示d与R,r的关系相交____________内切________内含________|R-r|1),若两圆相交,则r的取值范围是.(3)若圆O1：x2+y2=4与圆O2：(x-a)2+y2=1外切,则a=______.\n【解析】(1)因为R=5,r=2,d=3,所以d=R-r,所以两圆内切.答案：内切(2)因为圆心距d=|O1O2|=2,且两圆相交,所以r-10)的公共弦长为2,则a=.2.(2013·烟台高一检测)已知两圆C1：x2+y2-2x-6y+1=0和圆C2：x2+y2-10x-12y+45=0.求两圆的公共弦所在直线的方程和公共弦的长.\n【解题指南】1.先求出公共弦所在的直线方程,利用圆x2+y2=4的半径和圆心到直线的距离及半弦长求解.2.先求两圆的公共弦所在的直线方程,然后求圆心C1到公共弦所在直线的距离d,最后利用公共弦的长即可得解.\n【解析】1.两圆方程作差知公共弦所在直线方程为如图.由已知得|AC|=，｜OA｜=2.因为a>0,所以|OC|＝=1,所以a=1.答案：1\n2.设两圆的交点为A(x1,y1)，B(x2,y2)，则A，B两点满足方程组将两个方程相减得4x+3y-22=0，即为两圆公共弦所在直线的方程.易知圆C1的圆心(1，3)，半径r=3，则点C1到直线4x+3y-22=0的距离故公共弦AB的长为\n【技法点拨】求两圆公共弦长及公共弦所在直线的方程的两种方法(1)方法一：解方程组求出两圆交点坐标,然后由两点间距离公式求弦长,由两点坐标求公共弦所在直线方程.本方法运算量较大,一般不常用.(2)方法二：\n【变式训练】已知圆O：x2+y2=25和圆C：x2+y2-4x-2y-20=0相交于A,B两点,求公共弦AB的长.【解析】两圆方程相减得弦AB所在直线的方程为4x+2y-5=0.圆O：x2+y2=25的圆心到直线AB的距离所以公共弦AB的长为|AB|=\n类型三与两圆相切有关的问题通过解答与两圆相切有关的问题,试总结处理两圆相切问题的两个步骤.1.(2013·哈尔滨高二检测)半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是()A.(x-4)2+(y-6)2=6B.(x+4)2+(y-6)2=6或(x-4)2+(y-6)2=6C.(x-4)2+(y-6)2=36D.(x+4)2+(y-6)2=36或(x-4)2+(y-6)2=36\n2.求与圆x2+y2-2x=0外切且与直线x+y=0相切于点M(3,-)的圆的方程.\n【解题指南】1.已知半径,确定圆的方程的关键是确定圆心坐标.2.两圆外切时圆心距等于两半径之和,当直线与圆相切时圆心到直线的距离等于圆的半径长,据此列方程组求解.\n【解析】1.选D.由题意可设圆的方程为(x-a)2+(y-6)2=36，由题意，得所以a2=16,所以a=±4.\n2.设所求圆的方程为(x-a)2+(y-b)2=r2(r＞0),由题知所求圆与圆x2+y2-2x=0外切，则=r+1.①又所求圆过点M(3，-)的切线为直线x+y=0,故②③解由①②③组成的方程组得a=4,b=0,r=2或a=0,b=,r=6.故所求圆的方程为(x-4)2+y2=4或x2+(y+)2=36.\n【技法点拨】处理两圆相切问题的两个步骤(1)定性，即必须准确把握是内切还是外切，若只是告诉相切，则必须分两圆内切、外切两种情况讨论.(2)转化思想，即将两圆相切的问题转化为两圆的圆心距等于两圆半径之差的绝对值(内切时)或两圆半径之和(外切时).\n【变式训练】求和圆(x-2)2+(y+1)2=4相切于点(4,-1)且半径为1的圆的方程.\n【解析】设所求圆的圆心为P(a,b)，所以①(1)若两圆外切，则有②由①②，解得a=5,b=-1.所以所求圆的方程为(x-5)2+(y+1)2=1.\n(2)若两圆内切，则有③由①③,解得a=3,b=-1.所以所求圆的方程为(x-3)2+(y+1)2=1.综上可知,所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.\n1.圆C1：x2+y2-4x=0和C2：x2+y2+4y=0的位置关系是()A.外切B.相离C.内切D.相交【解析】选D.两圆化为标准方程为：圆C1：(x-2)2+y2=4,圆C2：x2+(y+2)2=4,所以r1=r2=2,d=|C1C2|因此|r2-r1|+1,所以a2+b2>3+2.答案：a2+b2>3+2\n6.判断下列两圆的位置关系.(1)(x+2)2+(y-2)2=1和(x-2)2+(y-5)2=16.(2)x2+y2+6x-7=0和x2+y2+6y-27=0.\n【解析】(1)根据题意得,两个圆的半径分别为r1=1和r2=4,两圆的圆心距d=r1+r2,所以两圆外切.(2)将圆的一般方程化为标准方程,得(x+3)2+y2=16,x2+(y+3)2=36.故两圆的半径分别为r1=4和r2=6,两圆的圆心距显然2<<10,即|r1-r2|

您可能关注的文档

相关文档

最近下载