【教案】高中数学《函数图象的变换》教案 4页

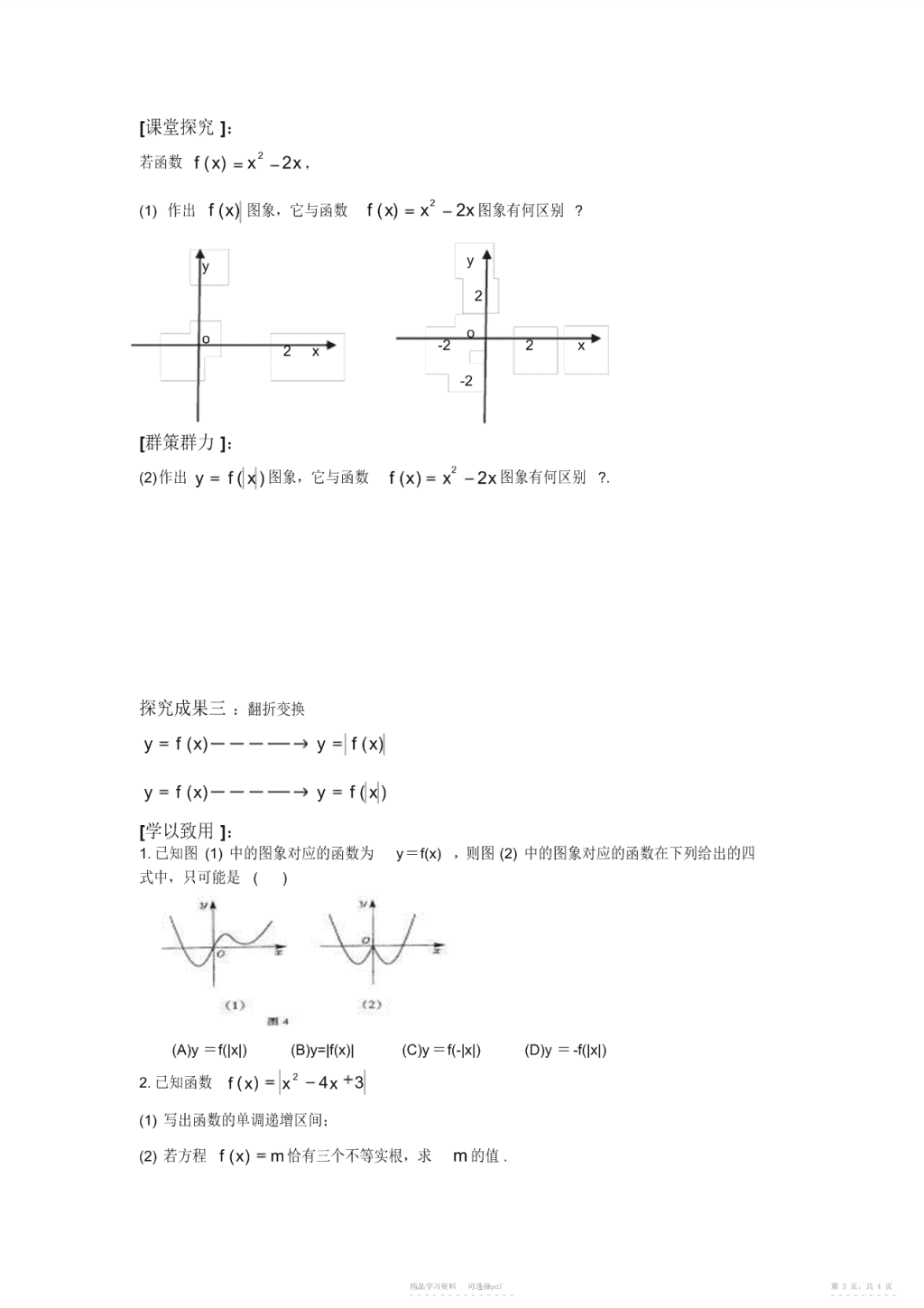
函数图象的变换[学习目标]：1.能利用一次函数、二次函数、反比例函数图象按照图象变换法则作图.2.会对已知函数yf(x)图象进行平移、对称、翻折变换，画出yf(xc)、yf(x)c、yf(x)、yf(x)、yf(x)、yf(x)、yf(x)的图象3.能借助函数图象解决与函数性质相关的问题.4.在数学活动中感受数学思想方法之巧、体会数学思想方法之灵活；同时通过本节课的学习，培养数形结合的学习习惯和能力,培养学生主动学习、合作交流的意识.[课前准备]：2已知函数f(x)x,2(1)求f(x)2,f(x)2，并画出其图象，指出它与函数f(x)x有何区别？2(2)求f(x)2，f(x)2并画出其图象，指出它与函数f(x)x有何区别？yy22oo-22x-22x-2-2[课堂探究]：如何由函数yf(x)的图象得到函数yf(xc)的图象？函数yf(x)c的图象呢？探究成果一：平移变换yf(x)yf(xc)yf(x)yf(x)c精品学习资料可选择pdf第1页，共4页-----------------------\n[学以致用]：11.函数g(x)1的图象的对称中心为().x22.函数yx1的单调递减区间是.[课堂探究]：若函数f(x)x1，请画出函数yf(x)图象，两函数图象有什么关系?y1o-11x-1探究成果二：对称变换yf(x)yf(x)yf(x)yf(x)yf(x)yf(x)[学以致用]:11.与曲线y关于原点对称的曲线为（）x11111A．yB．yC．yD．y1x1x1x1x2.函数y1x1的图象与x轴所围成的封闭图形的面积为精品学习资料可选择pdf第2页，共4页-----------------------\n[课堂探究]：2若函数f(x)x2x，2(1)作出f(x)图象，它与函数f(x)x2x图象有何区别?yy2oo-22x2x-2[群策群力]：2(2)作出yf(x)图象，它与函数f(x)x2x图象有何区别?.探究成果三：翻折变换yf(x)yf(x)yf(x)yf(x)[学以致用]：1.已知图(1)中的图象对应的函数为y＝f(x)，则图(2)中的图象对应的函数在下列给出的四式中，只可能是()(A)y＝f(|x|)(B)y=|f(x)|(C)y＝f(-|x|)(D)y＝-f(|x|)22.已知函数f(x)x4x3(1)写出函数的单调递增区间；(2)若方程f(x)m恰有三个不等实根，求m的值.精品学习资料可选择pdf第3页，共4页-----------------------\n[盘点收获]如何由yf(x)的图象得到下列函数的图象?yf(xc)yf(x)cyf(x)yf(x)yf(x)yf(x)yf(x)检验成果：11.函数y的图象是（）x1yyyyO-11x-1OxO1xxO-1（A）（B）（C）（D）2.函数f(x)是R上的减函数，A(0,1),B(3,-1)是图象上的两点，则∣f(x)∣<1的解集是3.已知f(x)为定义在R上的偶函数,当x,0[)时,f(x)x1，则f(x)10的解集为精品学习资料可选择pdf第4页，共4页-----------------------