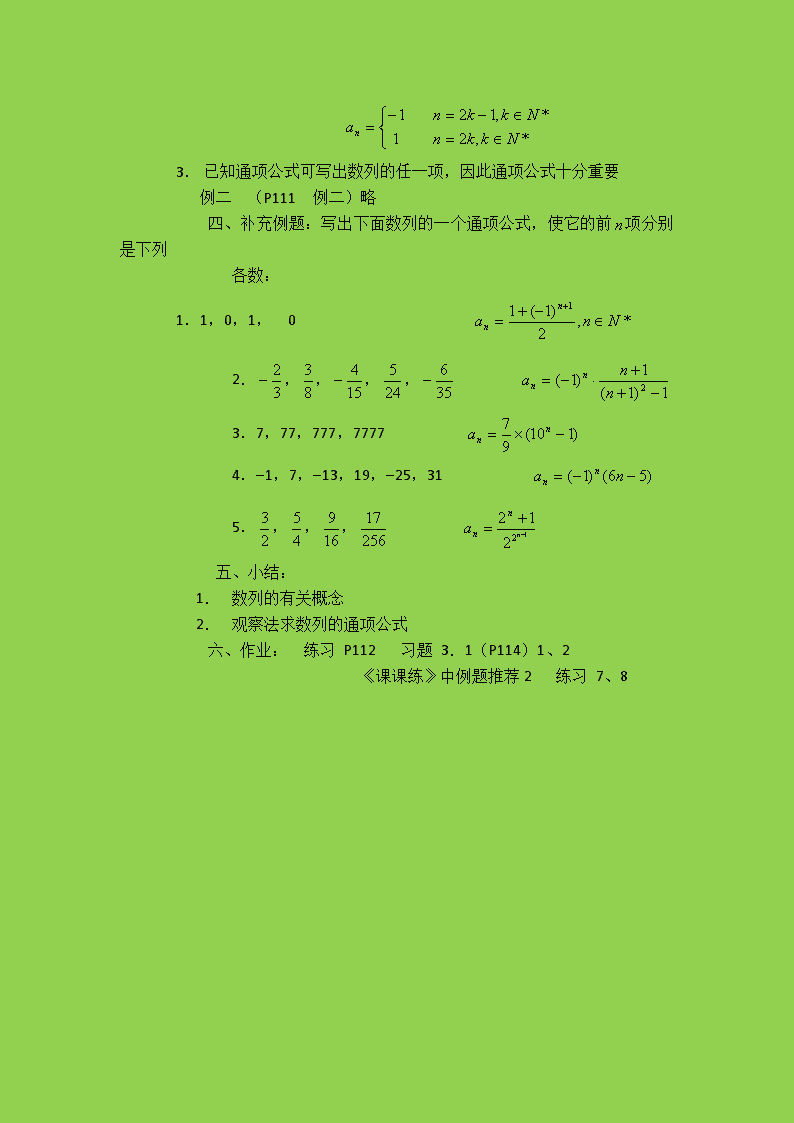高中数学数列教案一 7页

第三章数列第一教时教材：数列、数列的通项公式目的：要求学生理解数列的概念及其几何表示，理解什么叫数列的通项公式，给出一些数列能够写出其通项公式，已知通项公式能够求数列的项。过程：一、从实例引入（P110）1．堆放的钢管4,5,6,7,8,9,102．正整数的倒数3．4．-1的正整数次幂：-1,1,-1,1,…5．无穷多个数排成一列数：1,1,1,1,…二、提出课题：数列1．数列的定义：按一定次序排列的一列数（数列的有序性）2．名称：项，序号，一般公式，表示法3．通项公式：与之间的函数关系式如数列1：数列2：数列4：4．分类：递增数列、递减数列；常数列；摆动数列；有穷数列、无穷数列。5．实质：从映射、函数的观点看，数列可以看作是一个定义域为正整数集N*（或它的有限子集{1，2，…，n}）的函数，当自变量从小到大依次取值时对应的一列函数值，通项公式即相应的函数解析式。6．用图象表示：—是一群孤立的点例一（P111例一略）三、关于数列的通项公式1．不是每一个数列都能写出其通项公式（如数列3）2．数列的通项公式不唯一如数列4可写成和\n1．已知通项公式可写出数列的任一项，因此通项公式十分重要例二（P111例二）略四、补充例题：写出下面数列的一个通项公式，使它的前项分别是下列各数：1．1，0，1，02．，，，，3．7，77，777，77774．-1，7，-13，19，-25，315．，，，五、小结：1．数列的有关概念2．观察法求数列的通项公式六、作业：练习P112习题3．1（P114）1、2《课课练》中例题推荐2练习7、8\n第二教时教材：数列的递推关系目的：要求学生进一步熟悉数列及其通项公式的概念；了解数列递推公式的意义，会根据给出的递推公式写出数列的前n项。过程：一、复习：数列的定义，数列的通项公式的意义（从函数观点出发去刻划）二、例一：若记数列的前n项之和为Sn试证明：证：显然时，当即时∴∴注意：1°此法可作为常用公式2°当时满足时，则例二：已知数列的前n项和为①②求数列的通项公式。解：1．当时，当时，经检验时也适合2．当时，当时，∴三、递推公式（见课本P112-113略）以上一教时钢管的例子\n从另一个角度，可以：“递推公式”定义：已知数列的第一项，且任一项与它的前一项（或前项）间的关系可以用一个公式来表示，这个公式就叫做这个数列的递推公式。例三（P113例三）略例四已知，求．解一：可以写出：，，，，……观察可得：解二：由题设：∴∴例五已知，求．解一：观察可得：解二：由∴即∴∴四、小结：由数列和求通项\n递推公式（简单阶差、阶商法）五、作业：P114习题3．13、4《课课练》P116-118课时2中例题推荐1、2课时练习6、7、8\n第三教时教材：等差数列（一）目的：要求学生掌握等差数列的意义，通项公式及等差中项的有关概念、计算公式，并能用来解决有关问题。过程：一、引导观察数列：4，5，6，7，8，9，10，……3，0，-3，-6，……，，，，……12，9，6，3，……特点：从第二项起，每一项与它的前一项的差是常数—“等差”二、得出等差数列的定义：（见P115）注意：从第二项起，后一项减去前一项的差等于同一个常数。1．名称：AP首项公差2．若则该数列为常数列3．寻求等差数列的通项公式：由此归纳为当时（成立）注意:1°等差数列的通项公式是关于的一次函数2°如果通项公式是关于的一次函数，则该数列成AP证明：若它是以为首项，为公差的AP。3°公式中若则数列递增，则数列递减4°图象：一条直线上的一群孤立点三、例题：注意在中，，，四数中已知三个可以求出另一个。例一（P115例一）例二（P116例二）注意：该题用方程组求参数例三（P116例三）此题可以看成应用题\n四、关于等差中项：如果成AP则证明：设公差为，则∴例四《教学与测试》P77例一：在-1与7之间顺次插入三个数使这五个数成AP，求此数列。解一：∵∴是-1与7的等差中项∴又是-1与3的等差中项∴又是1与7的等差中项∴解二：设∴∴所求的数列为-1，1，3，5，7五、小结：等差数列的定义、通项公式、等差中项六、作业：P118习题3．21-9