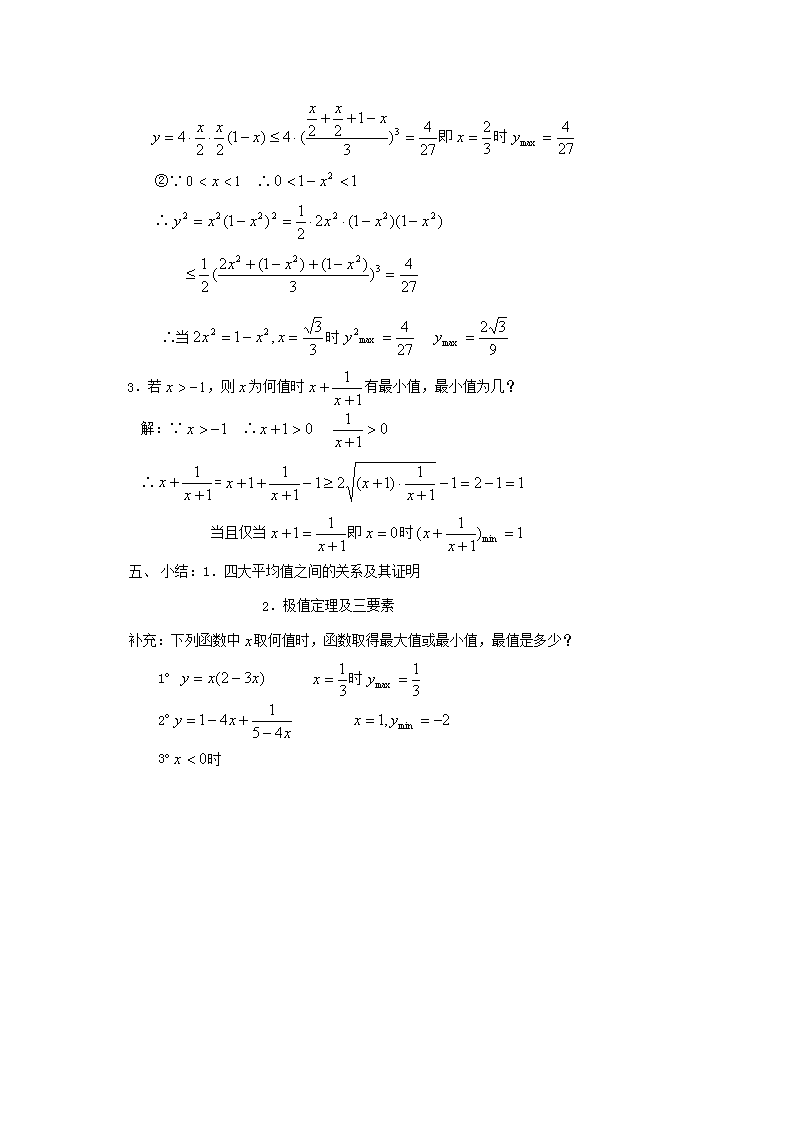高中数学 不等式课时复习教案04 教案 3页

第四教时不等式教材：极值定理目的：要求学生在掌握平均不等式的基础上进而掌握极值定理，并学会初步应用。过程：一、复习：算术平均数与几何平均数定义，平均不等式二、若，设求证：加权平均；算术平均；几何平均；调和平均证：∵∴即：（俗称幂平均不等式）由平均不等式即：综上所述：例一、若求证证：由幂平均不等式：三、极值定理已知都是正数，求证：1°如果积是定值，那么当时和有最小值2°如果和是定值，那么当时积有最大值\n证：∵∴1°当(定值)时，∴∵上式当时取“=”∴当时有2°当(定值)时，∴∵上式当时取“=”∴当时有注意强调：1°最值的含义（“≥”取最小值，“≤”取最大值）2°用极值定理求最值的三个必要条件：一“正”、二“定”、三“相等”一、例题1．证明下列各题：⑴证：∵∴于是⑵若上题改成，结果将如何？解：∵于是从而⑶若则解：若则显然有若异号或一个为0则∴2．①求函数的最大值②求函数的最大值解：①∵∴∴当即时\n即时②∵∴∴∴当时3．若，则为何值时有最小值，最小值为几？解：∵∴∴=当且仅当即时一、小结：1．四大平均值之间的关系及其证明2．极值定理及三要素补充：下列函数中取何值时，函数取得最大值或最小值，最值是多少？1°时2°3°时