【教案】高中数学新课立体几何教案3 6页

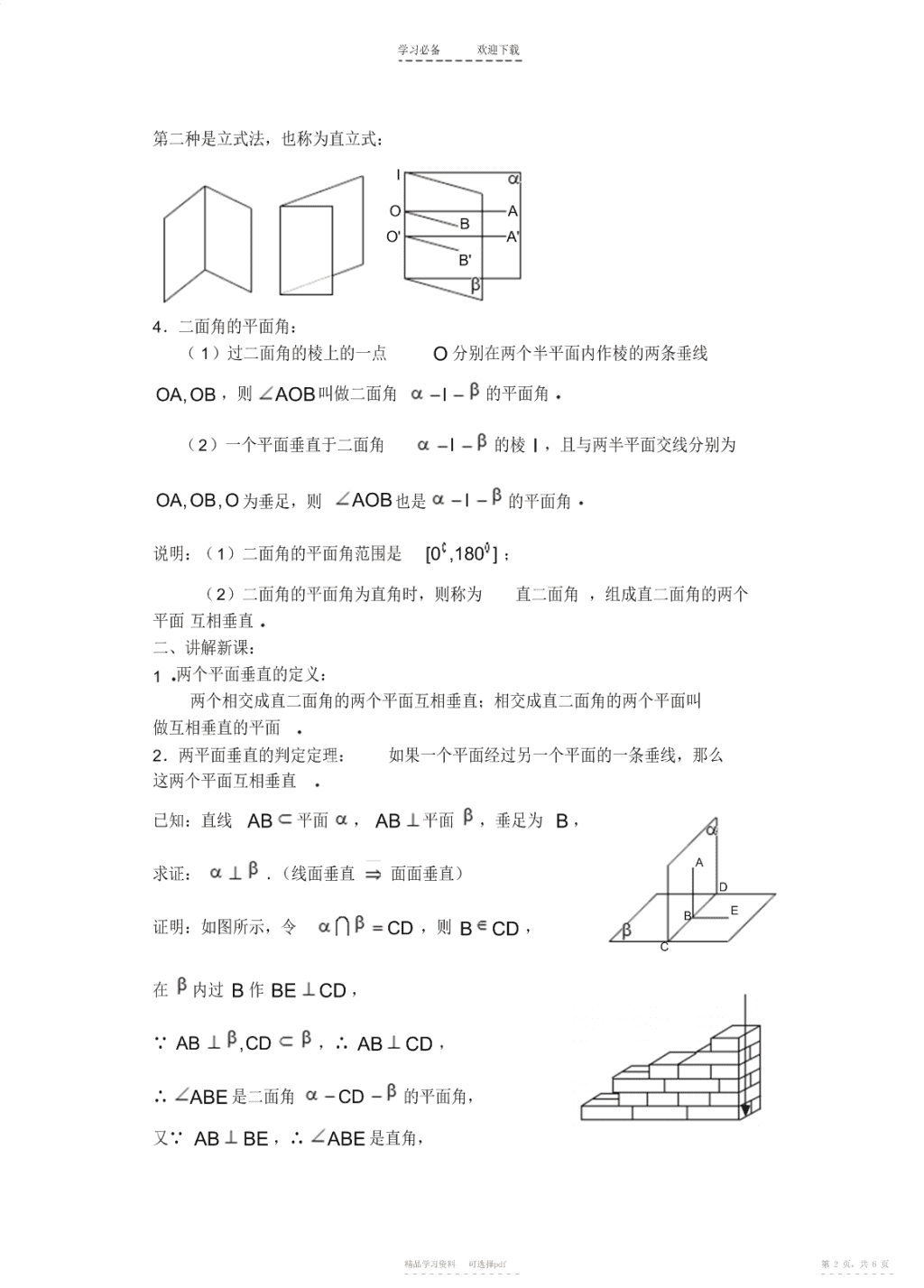
学习必备欢迎下载课题：9．7直线与平面所成的角和二面角(三)教学目的：1．两个平面垂直的定义、画法．2．两个平面垂直的判定定理．3．两个平面垂直的性质定理．理解面面垂直问题可能化为线面垂直的问题教学重点：两个平面垂直的判定和性质教学难点：两个平面垂直的判定及应用授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪教学过程：一、复习引入：1．直线和平面所成角（1）定义：平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角一直线垂直于平面，所成的角是直角一直线平行于平面或在平面内，所成角为0角直线和平面所成角范围：0，2（2）定理：斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角2．公式：已知平面的斜线a与内一直线b相交P成θ角，且a与相交成1角，a在上的射影ca与b相交成2角，则有cos1cos2cos1Ac2O3二面角的概念：平面内的一条直线把平面分为Bb两个部分，其中的每一部分叫做半平面；从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，每个半平面叫做二面角的面若棱为l，两个面分别为,的二面角记为l；二面角的图形表示：第一种是卧式法，也称为平卧式：KADGJELBICFH精品学习资料可选择pdf第1页，共6页-----------------------\n学习必备欢迎下载第二种是立式法，也称为直立式：lOABO'A'B'4．二面角的平面角：（1）过二面角的棱上的一点O分别在两个半平面内作棱的两条垂线OAOB,，则AOB叫做二面角l的平面角（2）一个平面垂直于二面角l的棱l，且与两半平面交线分别为OAOBO,,为垂足，则AOB也是l的平面角说明：（1）二面角的平面角范围是[0,180]；（2）二面角的平面角为直角时，则称为直二面角，组成直二面角的两个平面互相垂直二、讲解新课：1两个平面垂直的定义：两个相交成直二面角的两个平面互相垂直；相交成直二面角的两个平面叫做互相垂直的平面2．两平面垂直的判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直已知：直线AB平面，AB平面，垂足为B，A求证：．（线面垂直面面垂直）DEB证明：如图所示，令CD，则BCD，C在内过B作BECD，∵AB,CD，∴ABCD，∴ABE是二面角CD的平面角，又∵ABBE，∴ABE是直角，精品学习资料可选择pdf第2页，共6页-----------------------\n学习必备欢迎下载所以，与所成的二面角是直角，即．实例：建筑工地在砌墙时，常用铅垂的线来检查所砌的墙是否和水平面垂直3．两平面垂直的性质定理：若两个平面互相垂直，那么在一个平面内垂直于它们的交线的直线垂直于另一个平面已知：,CDAB,,ABCD于点B，求证：AB．（面面垂直线面垂直）证明：在内过B作BECD，则由题意得ABE是CD的平面角，∵知ABBE，又∵ABCD，∴AB．三、讲解范例：例1如图，已知AB是圆O的直径，PA垂直于O所在的平面，C是圆周上不同于,AB的任一点，求证：平面PAC平面PBC．分析：根据“面面垂直”的判定定理，要证明两平面互P相垂直，只要在其中一个平面中寻找一条与另一平面垂直的直线即可C解：∵AB是圆O的直径，∴ACBC，又∵PA垂直于O所在的平面，∴PABC，ABO∴BC平面PAC，又BC在平面PBC中，所以，平面PAC平面PBC．说明：由于平面PAC与平面PBC相交于PC，所以如果平面PAC平面PBC，则在平面PBC中，垂直于PC的直线一定垂直于平面PAC，这是寻找两个平面的垂线的常用方法例2．已知a,,，求证：a．证明：设AB,AC，在内取点P，过P作PMAB于M，PNAC于点N，∵，∴PM，a又∵a，∴PMa，同理可得PNa，MANBPC精品学习资料可选择pdf第3页，共6页-----------------------\n学习必备欢迎下载∴a．例3．已知在一个60的二面角的棱长有两点,AB，ACBD,C分别是在这个二面角的两个平面内，且垂直于线段AB，又知ABAB4cmAC,6cmBD,8cm，求CD的长解：由已知DCAABAB,BD,CABD,18060120，22222∴|CD|(CAABBD)|CA||AB||BD|268cos120222164826868，2|CD|217(cm)四、课堂练习：1．直角ABC的斜边AB在平面内，ACBC,与所成角分别为30,45，CD是斜边AB上的高线，求CD与平面所成角的正弦值解：过点C作CH于点H，连接AHBHOH,,，则CAH30，CBH45，CDH为所求CD与所成角，记为，令CHa，则AC2,aBC2a，CACBC23则在RtABC中，有CDaAB3HCH3在RtCDH中，sinADBCD23∴CD与平面所成角的正弦值.2精品学习资料可选择pdf第4页，共6页-----------------------\n学习必备欢迎下载2．如果二面角l的平面角是锐角，点P到,,l的距离分别为22,4,42，求二面角的大小AP分析：点P可能在二面角l内部，也可能CB在外部，应区别处理l图1解：如图1是点P在二面角l的内部时，图2是点P在二面角l外部时，∵PA∴PAl∵ACl∴面PAClP同理，面PBCl而面PAC面PBCPCA∴面PAC与面PBC应重合即ACPB,,,在同一平面内，BC则ACB是二面角l的平面角l图2PA221在RtAPC中，sinACPPB422∴ACP30PB42在RtBPC中，sinBCP∴BCP45PC422故ACB304575（图1）或ACB453015（图2）即二面角l的大小为75或15D'C'说明：作一个垂直于棱的平面，此平面与两个半平面的交线所B'成的角就是二面角的平面角A'3．如图，正方体的棱长为1，BCBC'O，求：O（1）AO与AC所成角；CD（2）AO与平面ABCD所成角的正切值；E（3）平面AOB与平面AOC所成角AB解：（1）∵AC//AC∴AO与AC所成角就是OAC精品学习资料可选择pdf第5页，共6页-----------------------\n学习必备欢迎下载∵OCOBAB,平面BC∴OCOA（三垂线定理）2在RtAOC中，OC,AC2∴OAC302（2）作OEBC，平面BC平面ABCD∴OE平面ABCD，OAE为OA与平面ABCD所成角12125OE5在RtOAE中，OE,AE1()∴tanOAE222AE5（3）∵OCOAOC,OB∴OC平面AOB又∵OC平面AOC∴平面AOB平面AOC即平面AOB与平面AOC所成角为90说明：本题包含了线线角，线面角和面面角三类问题，求角度问题主要是求两条异面直线所成角(0,]，直线和平面所成角[0,]，二面角[0,]三种；求角22度问题解题的一般步骤是：（1）找出这个角；（2）证明该角符合题意；（3）作出这个角所在的三角形，解三角形，求出角；求角度问题不论哪种情况都归结到两条直线所成角问题，即在线线成角中找到答案五、小结：1．两个平面垂直的定义、画法2．两个平面垂直的判定方法（判定方法有两种，一是利用定义，二是利用判定定理．）3．应用两个平面垂直的判定定理的关键是将面面垂直的问题转化为线面垂直的问题；4．两个平面垂直的性质.六、课后作业：七、板书设计（略）八、课后记：精品学习资料可选择pdf第6页，共6页-----------------------