【教案】高中数学函数单调性教案新人教版必修 5页

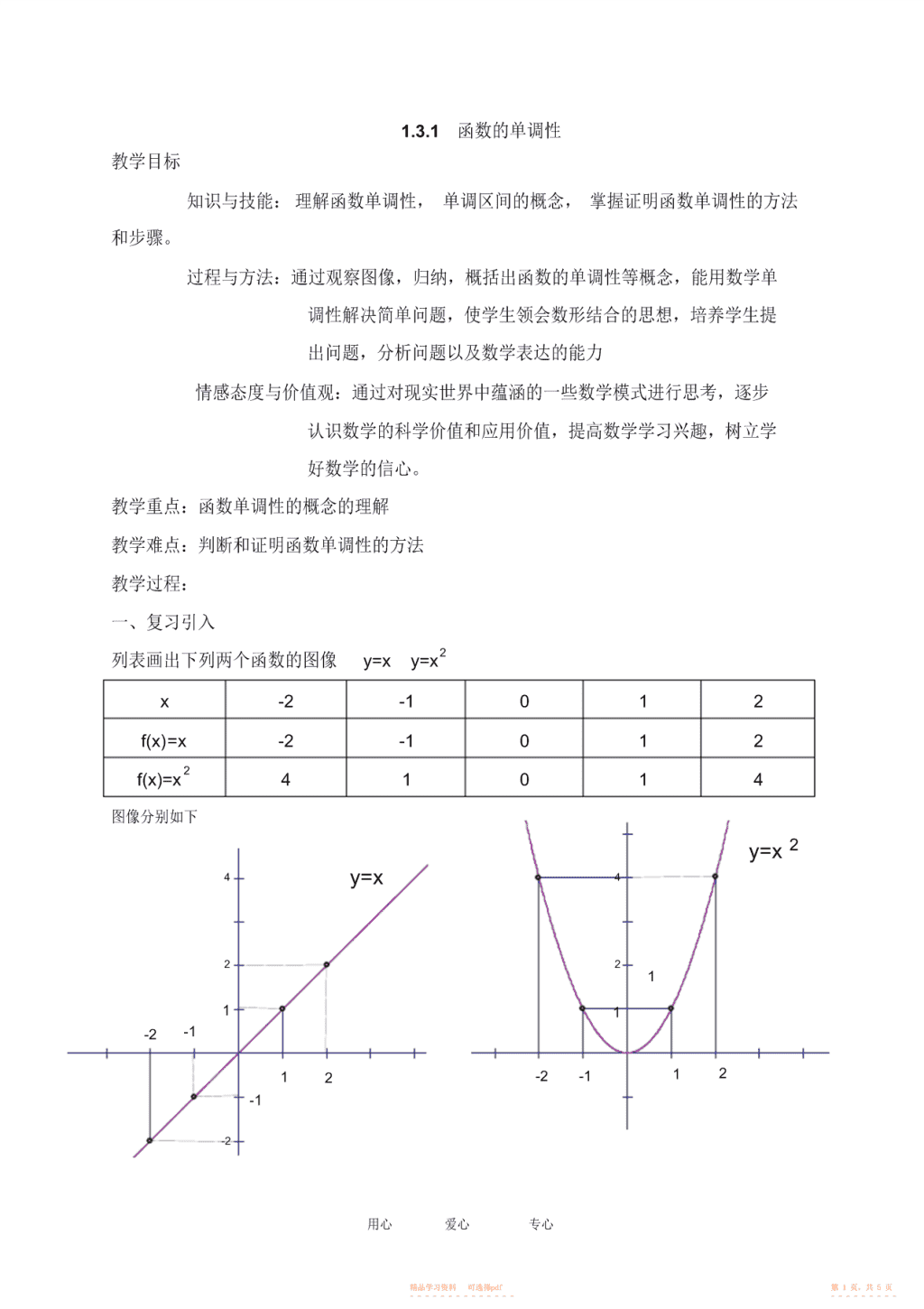
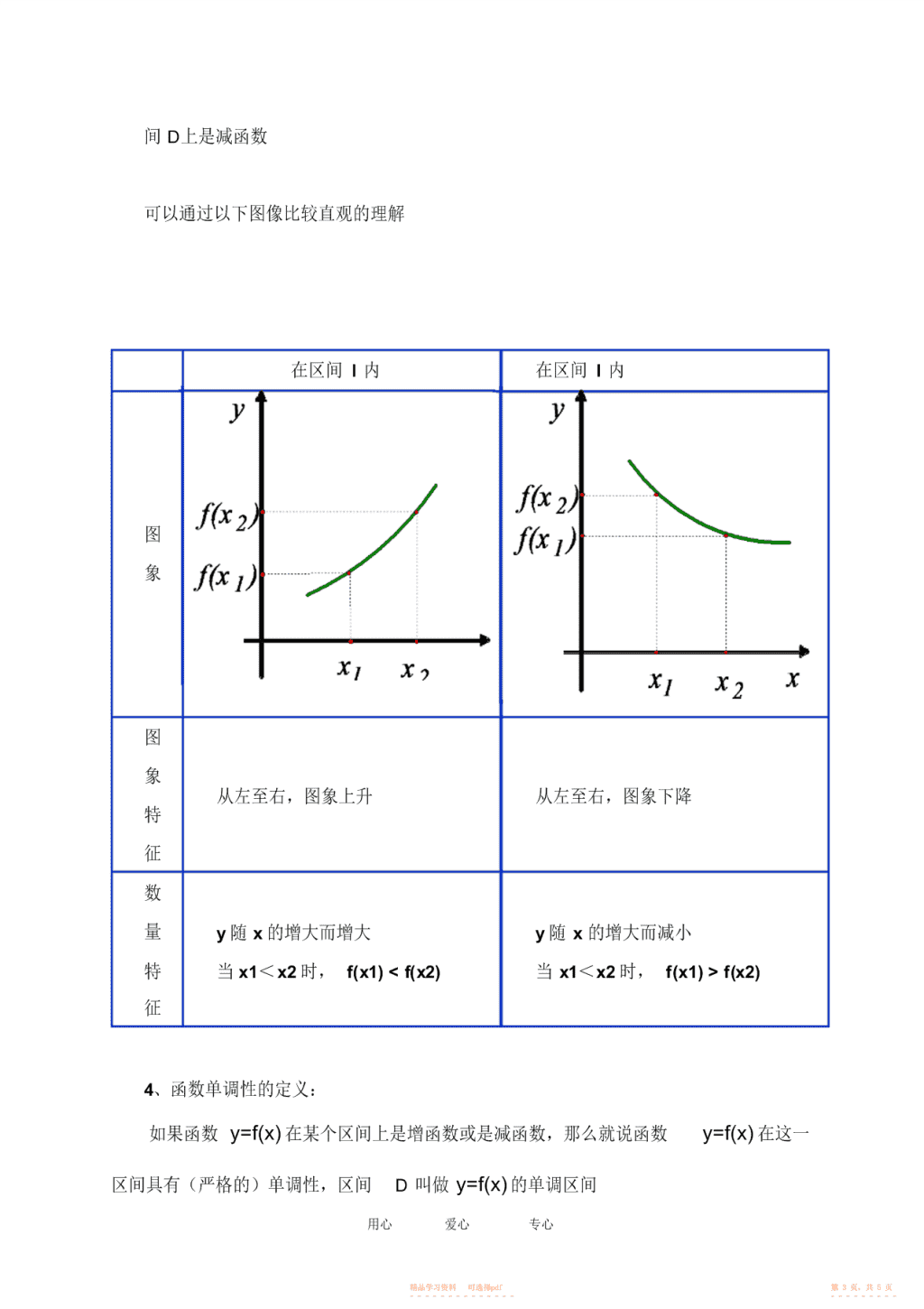
1.3.1函数的单调性教学目标知识与技能：理解函数单调性，单调区间的概念，掌握证明函数单调性的方法和步骤。过程与方法：通过观察图像，归纳，概括出函数的单调性等概念，能用数学单调性解决简单问题，使学生领会数形结合的思想，培养学生提出问题，分析问题以及数学表达的能力情感态度与价值观：通过对现实世界中蕴涵的一些数学模式进行思考，逐步认识数学的科学价值和应用价值，提高数学学习兴趣，树立学好数学的信心。教学重点：函数单调性的概念的理解教学难点：判断和证明函数单调性的方法教学过程：一、复习引入2列表画出下列两个函数的图像y=xy=xx-2-1012f(x)=x-2-10122f(x)=x41014图像分别如下y=x24y=x422111-2-112-2-112-1-2用心爱心专心精品学习资料可选择pdf第1页，共5页-----------------------\n观察表格，图像，找出x与y之间的关系（1）f(x)=x○1从左至右图象上升还是下降______?○2在区间____________上，随着x的增大，f(x)的值随着________．2（2）f(x)=x○1在区间____________上，f(x)的值随着x的增大而________．○2在区间____________上，f(x)的值随着x的增大而________．二、探究新知21、如函数f(x)=x在（0，+∞）上，y随着x的增大而增大，在区间（0，+∞）上，22任取两个x1，x2，得到f(x1)=x1f(x2)=x2，x1x2时，都有f(x1)>f(x2)，那么就说函数在f(x)在区用心爱心专心精品学习资料可选择pdf第2页，共5页-----------------------\n间D上是减函数可以通过以下图像比较直观的理解在区间I内在区间I内图象图象从左至右，图象上升从左至右，图象下降特征数量y随x的增大而增大y随x的增大而减小特当x1＜x2时，f(x1)f(x2)征4、函数单调性的定义：如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，区间D叫做y=f(x)的单调区间用心爱心专心精品学习资料可选择pdf第3页，共5页-----------------------\n三、例题讲解例1如图，是定义在闭区间[-5，5]上的函数yf(x)的图象，根据图象说出yf(x)的单调区间，以及在每一单调区间上，函数yf(x)是增函数还是减函数.y-5-2O135x解：函数yf(x)的单调区间有[-5，-2)，[-2，1)，[1，3)，[3，5]，其中yf(x)在区间[-5，-2)，[1，3)上是减函数，在区间[-2，1)，[3，5]上是增函数.k例2物理学中的玻意耳定律P=（k为正常数）告诉我们，对于一定量的气体，当其V体积V减少时，压强P将增大。试用函数的单调性证明之。k分析：按题意，只要证明函数P=在区间（0，+∞）上是减函数即可。V判断函数单调性的方法步骤利用定义证明函数f(x)在给定的区间D上的单调性的一般步骤：①任取x1，x2∈D，且x1