【教案】高中数学必修1《函数的单调性》教案 6页

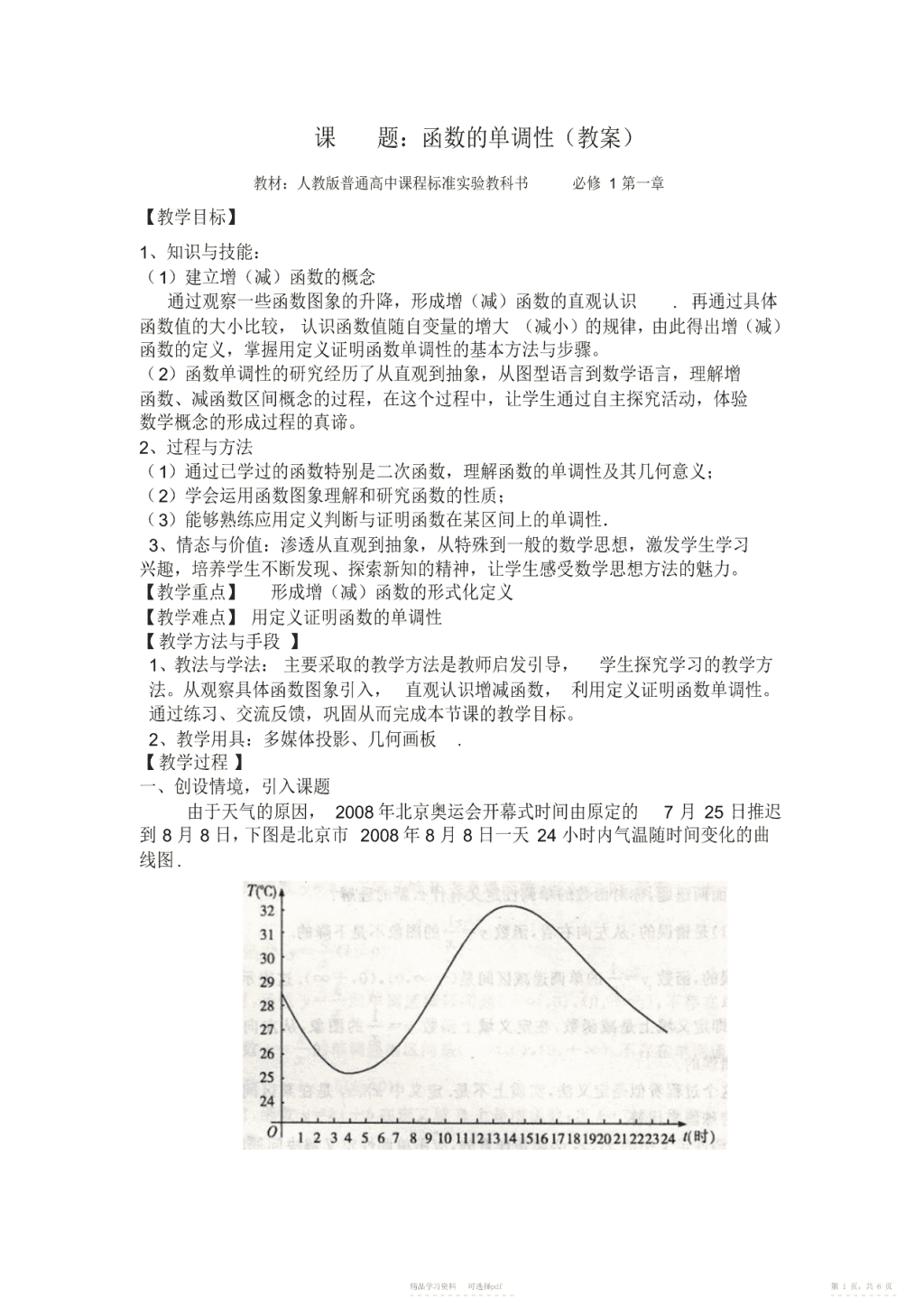
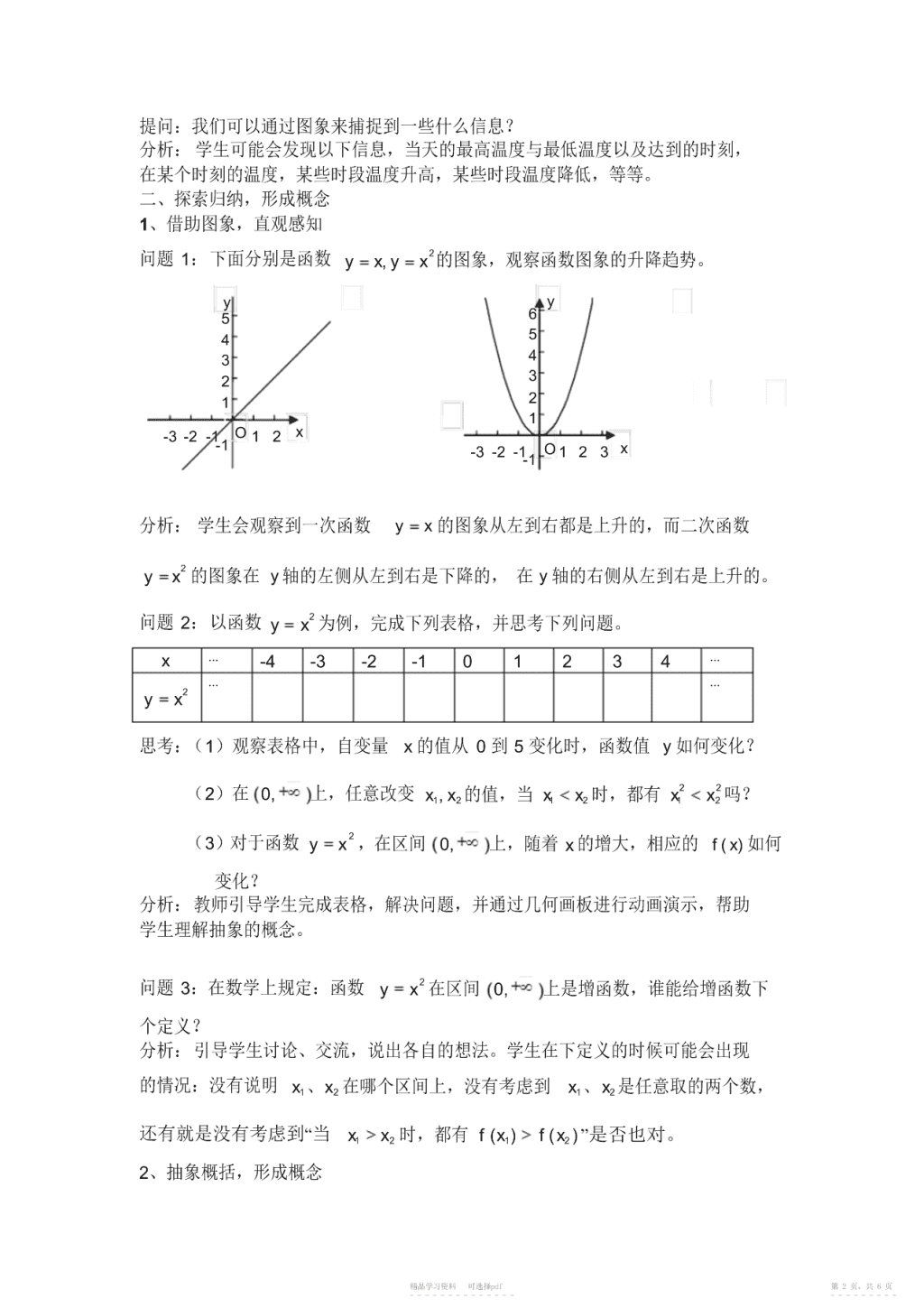
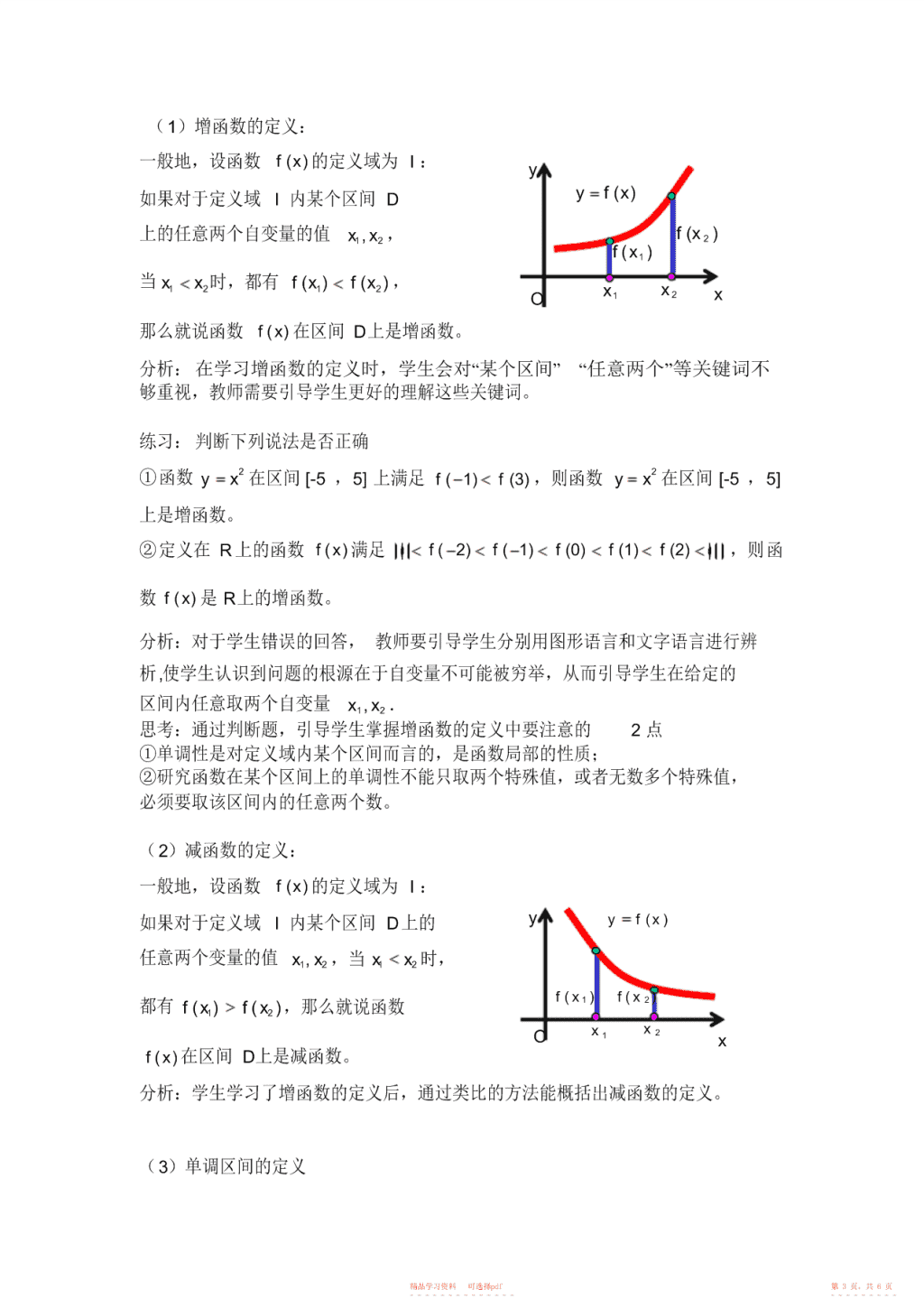
课题：函数的单调性（教案）教材：人教版普通高中课程标准实验教科书必修1第一章【教学目标】1、知识与技能：（1）建立增（减）函数的概念通过观察一些函数图象的升降，形成增（减）函数的直观认识.再通过具体函数值的大小比较，认识函数值随自变量的增大（减小）的规律，由此得出增（减）函数的定义，掌握用定义证明函数单调性的基本方法与步骤。（2）函数单调性的研究经历了从直观到抽象，从图型语言到数学语言，理解增函数、减函数区间概念的过程，在这个过程中，让学生通过自主探究活动，体验数学概念的形成过程的真谛。2、过程与方法（1）通过已学过的函数特别是二次函数，理解函数的单调性及其几何意义；（2）学会运用函数图象理解和研究函数的性质；（3）能够熟练应用定义判断与证明函数在某区间上的单调性．3、情态与价值：渗透从直观到抽象，从特殊到一般的数学思想，激发学生学习兴趣，培养学生不断发现、探索新知的精神，让学生感受数学思想方法的魅力。【教学重点】形成增（减）函数的形式化定义【教学难点】用定义证明函数的单调性【教学方法与手段】1、教法与学法：主要采取的教学方法是教师启发引导，学生探究学习的教学方法。从观察具体函数图象引入，直观认识增减函数，利用定义证明函数单调性。通过练习、交流反馈，巩固从而完成本节课的教学目标。2、教学用具：多媒体投影、几何画板.【教学过程】一、创设情境，引入课题由于天气的原因，2008年北京奥运会开幕式时间由原定的7月25日推迟到8月8日，下图是北京市2008年8月8日一天24小时内气温随时间变化的曲线图.精品学习资料可选择pdf第1页，共6页-----------------------\n提问：我们可以通过图象来捕捉到一些什么信息？分析：学生可能会发现以下信息，当天的最高温度与最低温度以及达到的时刻，在某个时刻的温度，某些时段温度升高，某些时段温度降低，等等。二、探索归纳，形成概念1、借助图象，直观感知2问题1：下面分别是函数yxy,x的图象，观察函数图象的升降趋势。yy56543432121-3-2-1O12x-1-3-2-1O123x-1分析：学生会观察到一次函数yx的图象从左到右都是上升的，而二次函数2yx的图象在y轴的左侧从左到右是下降的，在y轴的右侧从左到右是上升的。2问题2：以函数yx为例，完成下列表格，并思考下列问题。x⋯-4-3-2-101234⋯2⋯⋯yx思考：（1）观察表格中，自变量x的值从0到5变化时，函数值y如何变化？22（2）在0,上，任意改变xx1,2的值，当x1x2时，都有x1x2吗？2（3）对于函数yx，在区间0,上，随着x的增大，相应的fx()如何变化？分析：教师引导学生完成表格，解决问题，并通过几何画板进行动画演示，帮助学生理解抽象的概念。2问题3：在数学上规定：函数yx在区间0,上是增函数，谁能给增函数下个定义？分析：引导学生讨论、交流，说出各自的想法。学生在下定义的时候可能会出现的情况：没有说明x1、x2在哪个区间上，没有考虑到x1、x2是任意取的两个数，还有就是没有考虑到“当x1x2时，都有fx()1fx(2)”是否也对。2、抽象概括，形成概念精品学习资料可选择pdf第2页，共6页-----------------------\n（1）增函数的定义：一般地，设函数fx()的定义域为I：yy)x(f如果对于定义域I内某个区间D上的任意两个自变量的值xx1,2，x(f2)x(f1)当xx时，都有fx()fx()，1212xx2O1x那么就说函数fx()在区间D上是增函数。分析：在学习增函数的定义时，学生会对“某个区间”“任意两个”等关键词不够重视，教师需要引导学生更好的理解这些关键词。练习：判断下列说法是否正确22①函数yx在区间[-5，5]上满足f(1)f(3)，则函数yx在区间[-5，5]上是增函数。②定义在R上的函数f(x)满足f(2)f(1)f(0)f(1)f(2)，则函数fx()是R上的增函数。分析：对于学生错误的回答，教师要引导学生分别用图形语言和文字语言进行辨析,使学生认识到问题的根源在于自变量不可能被穷举，从而引导学生在给定的区间内任意取两个自变量x1,x2．思考：通过判断题，引导学生掌握增函数的定义中要注意的2点①单调性是对定义域内某个区间而言的，是函数局部的性质；②研究函数在某个区间上的单调性不能只取两个特殊值，或者无数多个特殊值，必须要取该区间内的任意两个数。（2）减函数的定义：一般地，设函数fx()的定义域为I：如果对于定义域I内某个区间D上的yyx(f)任意两个变量的值xx1,2，当x1x2时，(fx1)(fx2)都有fx()1fx(2)，那么就说函数Ox1x2xfx()在区间D上是减函数。分析：学生学习了增函数的定义后，通过类比的方法能概括出减函数的定义。（3）单调区间的定义精品学习资料可选择pdf第3页，共6页-----------------------\n如果函数yfx()在区间D上是增函数或减函数，那么就说函数yfx()在这一区间具有（严格的）单调性，区间D叫做yfx()的单调区间。三、巩固基础，演练提升1、例题例1如图是定义在区间[－5，5]上的函数y=f(x)，根据图象说出函数的单调区间，以及在每一单调区间上，它是增函数还是减函数？分析：教师提示利用函数单调性的几何意义，学生先思考或讨论后再回答，教师点拨、提示并及时评价学生。图象上升则在此区间上是增函数，图象下降则在此区间上是减函数。另外，教师还要提醒学生注意单调区间的书写。k例2物理学中的玻意耳定律P=（k为正常数）告诉我们，对于一定量的气体，V当其体积V减少时，压强P将增大。试用函数的单调性证明之。分析：学生先思考或讨论，再到黑板上书写，当学生没有证明思路时，教师再提示，及时纠正学生解答过程出现的问题，并标出关键的地方，以便学生总结定义法的步骤。最后教师指出，已知函数的解析式判断函数的单调性时，常用单调性的定义来解决。2、练习（1）画出下列函数的图象，并根据图象说出函数yfx()的单调区间，以及在各单调区间上函数yfx()是增函数还是减函数。22①yx4x4②y3x（2）证明函数fx()2x1在R上是减函数。分析：在第1题的教学中，教师让学生出黑板画出函数的图象，并且根据单调性的几何意义写出单调区间。第2题可以让学生先画出函数的图象，体会一下函数的单调性，再用单调性的定义证明。让学生掌握判断函数单调性的两种方法：图象法与定义法。精品学习资料可选择pdf第4页，共6页-----------------------\n四、归纳小结，提高认识1、小结（1）通过增（减）函数概念的形成，你学习到了什么？（2）增（减）函数的图象有什么特点？如何根据图象指出单调区间？（3）怎样用定义证明函数的单调性？分析：以问题的形式出现，引导学生回顾单调性定义的探究过程，回顾用定义证明函数单调性的步骤，鼓励学生积极回答，然后老师再从知识点及数学思想方法两方面总结．2、作业（必做题）<1>根据下图说出函数的单调区间，以及在每一单调区间上，函数是增函数还是减函数。y-1O245x<2>证明：2①函数fx()x1在(,0)上是减函数1②函数fx()1在(,0)上是增函数x（选做题）研究一次函数ymxbx(R)的单调性，并证明你的结论。板书设计1、增函数的定义例1、练习1、2、减函数的定义例2、练习2、3、单调区间精品学习资料可选择pdf第5页，共6页-----------------------\n课题：函数的单调性（教案说明）教材：人教版普通高中课程标准实验教科书必修1第一章“函数单调性”是一个重要的数学概念，本设计致力于展示概念是如何生成的，在概念的发生、发展中，通过层层设问，调动学生的思维，突出培养学生的思维能力，体现教师是如何活用教材。对于函数单调性，学生的认知困难主要在两个方面：（1）用准确的数学符号语言刻画图象的上升与下降，这种由形到数的翻译，从直观到抽象的转变对高一的学生是比较困难的；（2）单调性的证明是学生在函数内容中首次接触到的代数论证内容，而学生在代数方面的推理论证能力是比较薄弱的．根据以上的分析和教学大纲的要求，确定了本节课的重点和难点．围绕本节课的重点和难点，并根据学生现有的认知水平和心理特征，教师在教学的过程中注意到以下几个方面：（1）在探索概念阶段,让学生经历从直观到抽象、从特殊到一般、从感性到理性的认知过程，使得学生对概念的认识不断深入．（2）注重课堂问题的设计．通过让学生思考、讨论并解决问题，使得学生对函数的单调性有更加深刻的理解。（3）在应用概念阶段,通过对证明过程的分析，帮助学生掌握用定义证明函数单调性的方法和步骤．另外，根据本节课的特点，本节课使用多媒体投影和教具来辅助教学，为学生提供直观感性的材料，有助于学生对问题的理解和认识．精品学习资料可选择pdf第6页，共6页-----------------------