- 95.20 KB
- 2022-08-15 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
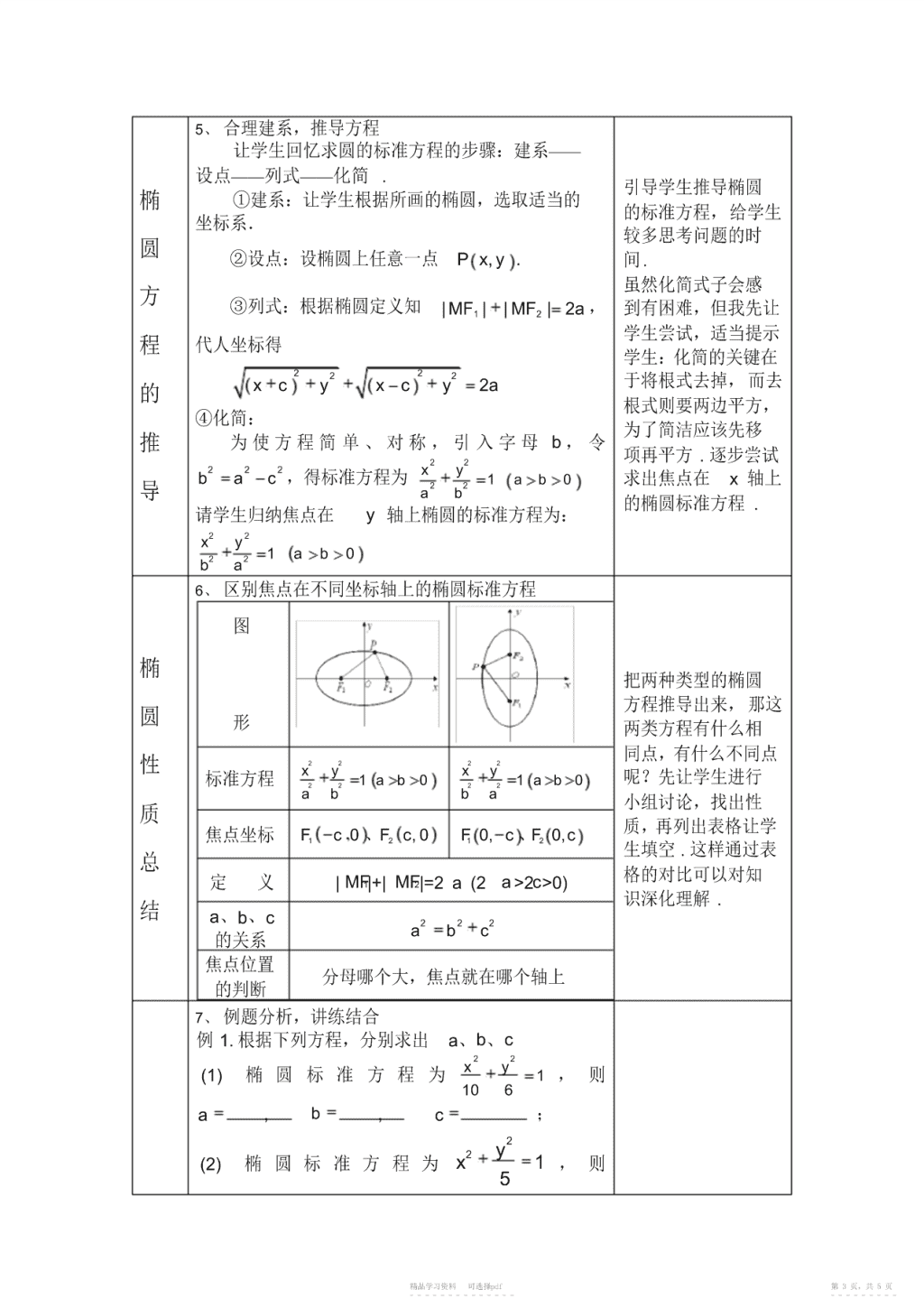
课题:椭圆的标准方程教材:人教版高中选修1-1(一)教材分析一.教材地位《椭圆的标准方程》是继学习必修2圆以后又一个二次曲线的实例.从知识上说,它是对前面所学的运用坐标法研究曲线的又一次实际演练,同时它也是进一步研究椭圆几何性质和双曲线、抛物线的基础;从方法上说,它为我们后面研究双曲线、抛物线这两种圆锥曲线提供了基本模式和方法.椭圆的标准方程是圆锥曲线方程研究的基础,它的学习方法对整个这一章具有导向和引领作用.二.教材特点1、由于本章节难度教大,学生普遍觉得比较困难.特别是缺乏数形结合能力,不善于简化平面几何问题.2、本章节的概念比较多,性质又比较相似,容易互相干扰而影响学习效果.三.教学重点、难点教学重点:掌握椭圆的定义及其标准方程;求椭圆标准方程的方法.教学难点:椭圆标准方程的推导和应用.(二)目的分析1.知识与技能目标:学习椭圆的标准方程及其应用;培养学生的数形结合的思想.2.过程与方法目标:通过椭圆定义,学生自主推导标准方程;通过观察图形逐渐培养学生对称的思想.3.情感态度与价值观:引导学生积极参与学习活动,培养学生的好奇心和学习兴趣;体验学习数学的成功与快乐,增强自信心.(三)、教法分析1、教法及设计目的应用实物模型导入新课,目的是要激发学生学习的兴趣,让他们观察椭圆的由来.在推导椭圆的标准方程时利用演示板来进行演示,先给学生直观的感性的认识.接着进行标准方程的推导,这样有利于培养学生的数形结合的能力.本课主要采用探究式教学方法,即“观察对象-问题引导-讨论探究-得出结论”的探究式教学方法.在教学上是以多媒体和演示板作为教学手段,始终坚持启发式教学,以学生为主体,引导学生思考并自己动手分析.2、学法及设计目的由于高二的学生思维比较活跃,又有了相应的知识基础,所以他们乐于探索新知识,虽然学习热情时起时落,但能在老师的引导下开展学习活动.在学习过程中可以安排学生进行小组讨论,注意要多利用定义来理解,要习惯动手画图,可以用类比法来记忆知识点.(四)、过程分析精品学习资料可选择pdf第1页,共5页-----------------------\n教学教学程序设计意图环节先用生活中的图片1、创设情境,引入课题来介绍,例如彗星运认图片展示生活中的椭圆行轨道等等这些例子来引出课题.识椭通过动画演示向学生说明椭圆的具体圆2、观察图形,探求规律画法,更直观形象.课件动态演示椭圆的形成过程让学生体会在变化中的变与不变及其内在联系.给学生提供一个动画手操作,合作学习的机会;通过实验让学出3、动手实验,亲身体会生去探究“满足什让学生拿出课前准备的硬纸板、细线、铅笔,同桌么样的条件下的点椭一起合作画椭圆的集合为椭圆”;让每个人都动手画图,圆自己思考问题,由此培养学生的自信心.4、归纳定义,学习定义(1)由学生画图及教师演示椭圆的形成过程,引导学生归纳椭圆的定义.定定义:平面内与两个定点F1、F2的距离之和等于常让学生通过反思画图数(大于∣F1F2∣)的点的轨迹叫椭圆.这两个过程,归纳定义,学义定点叫椭圆的焦点,两焦点的距离叫椭圆的焦习定义,为后面分析距.椭圆的标准方程做下椭(2)椭圆定义的再认识铺垫;比较深入地理问题:为什么要满足2a>2c呢?(1)当2a=2c时轨解椭圆定义的条件.圆迹是什么?(2)当2a<2c时轨迹又是什么?结论:(1)当2a>∣F1F2∣时,是椭圆;(2)当2a=∣F1F2∣时,是线段;(3)当2a<∣F1F2∣时轨迹不存在.精品学习资料可选择pdf第2页,共5页-----------------------\n5、合理建系,推导方程让学生回忆求圆的标准方程的步骤:建系——设点——列式——化简.引导学生推导椭圆椭①建系:让学生根据所画的椭圆,选取适当的的标准方程,给学生坐标系.较多思考问题的时圆②设点:设椭圆上任意一点Pxy.,间.虽然化简式子会感方③列式:根据椭圆定义知|MF1||MF2|2a,到有困难,但我先让学生尝试,适当提示程代人坐标得学生:化简的关键在2222xcyxcy2a于将根式去掉,而去的根式则要两边平方,④化简:为了简洁应该先移推为使方程简单、对称,引入字母b,令项再平方.逐步尝试22222xybac,得标准方程为1ab0求出焦点在x轴上22导ab的椭圆标准方程.请学生归纳焦点在y轴上椭圆的标准方程为:22xy221ab0ba6、区别焦点在不同坐标轴上的椭圆标准方程图椭把两种类型的椭圆方程推导出来,那这圆形两类方程有什么相同点,有什么不同点性2222xyxy呢?先让学生进行标准方程1ab01ab02222abba小组讨论,找出性质质,再列出表格让学焦点坐标F1c0、Fc2,0F10,c、F20,c生填空.这样通过表总格的对比可以对知定义|MF1|+|MF2|=2a(2a>2c>0)识深化理解.结a、b、c222abc的关系焦点位置分母哪个大,焦点就在哪个轴上的判断7、例题分析,讲练结合例1.根据下列方程,分别求出a、b、c22xy(1)椭圆标准方程为1,则106a,b,c;22y(2)椭圆标准方程为x1,则5精品学习资料可选择pdf第3页,共5页-----------------------\na,b,c;例1设计意图是:22加深学生对标准方(3)椭圆标准方程为x2y8,则程的理解和加深a、a,b,c.b、c关系式的应用.分析:本题的重点是第3小题,我提出3个问题:精①这个是不是标准方程②怎么化成标准方程③观察练习设计意图是:方程,分别求出a、b、c的值等于什么?第1题让学生自己讲学会将不同形式的方程转化成标准方程,可以对方分析,巩固定义.第程有更深刻的理解.2题已知a、b、c三精个量中的两个,只要书本课后练习P361、2确定焦点的位置就练22xy可以求出椭圆的方1.如果椭圆1上一点P到焦点F1的距离等10036程.并且与例1互为于6,那么点P到另一个焦点F2的距离是_____.逆向思维,可以加深2.写出适合下列条件的椭圆的标准方程:学生对方程和系数的理解.(1)a,4b1,焦点在x轴上;(2)a,4c15,焦点在x轴上.例2设计意图是:让学生巩固定义,学例2.已知椭圆两个焦点的坐标分别是F1()0,2、习求椭圆方程的方53法,学生要学会“先F1)0,2(并且经过点P(,);求它的标准方程.定位,再定量”.并22解法1:已知焦点,得出c;由定义,得出a;再由且学习了数形结合a、b、c的关系式得出b.由此解出方程.的思想,方程的思解法2:先设出方程,由焦点得c=2,列出a、b、c想.的关系式.运用方程的思想,联立方程组进行求解.解题时教师与学生一起分析题目,让学生观察焦点的位置,画出草图,设出方程.解题时可以安排小组讨论.而且要引起学生注意,a、b、c的关系式也是解决问题的一个重要条件,要学会运用好这个条件.8、巩固练习知变式题:1.已知椭圆的焦点在y轴上,且椭圆经过点P(-2,2)和Q(0,-3),求此椭圆的标准方程.识变式题:2.已知椭圆经过两个点P(-2,2)和巩Q(0,-3),求此椭圆的标准方程.这道题在设计上难通过引导分析:焦点分别在x轴和y轴时对应有不度逐步加深,目的是固同的方程,需要分2类来说明.要巩固知识,学习分与变式题1:与例2类似,可以让学生自主练习,巩类讨论的思想.固方程的求法和待定系数法.应变式题2:引导学生观察,两道题条件有什么不同?当椭圆的焦点不确定时,应该如何选择方程?是否用2类方程都适合呢?精品学习资料可选择pdf第4页,共5页-----------------------\n课本课主要探讨了椭圆定义并推导方程,掌握数最后进行课堂小形结合的思想,用定义法和待定系数法求椭圆的标结,先由学生小组讨堂准方程.论,再个别提问,然小本课的内容可用一句话概括为:一个定义,两后集体补充,最后教类方程,四种方法.师才引导和完善.结必做题:书本课后习题P422巩固椭圆标准方程作的相关知识.按照能当ab10c,25时,求椭圆的标准方程.力来选择作业也体业22现了分层教学的思xy布选做题:若方程1表示焦点在y轴想,还可以激发学生25m16m挑战自己的能力,激置上的椭圆,则m的取值范围是?发兴趣.(五)、评价分析这节课我使用了多媒体、演示板教学,激发学生的学习兴趣,使学生动手操作,学会探索.在教学中要关注到学生的基础薄弱,必须扎实基础,突出重点。在对学生评价时,不仅要看到学生学习的知识,更要肯定学生积极向上的态度和勇于探究的精神.精品学习资料可选择pdf第5页,共5页-----------------------