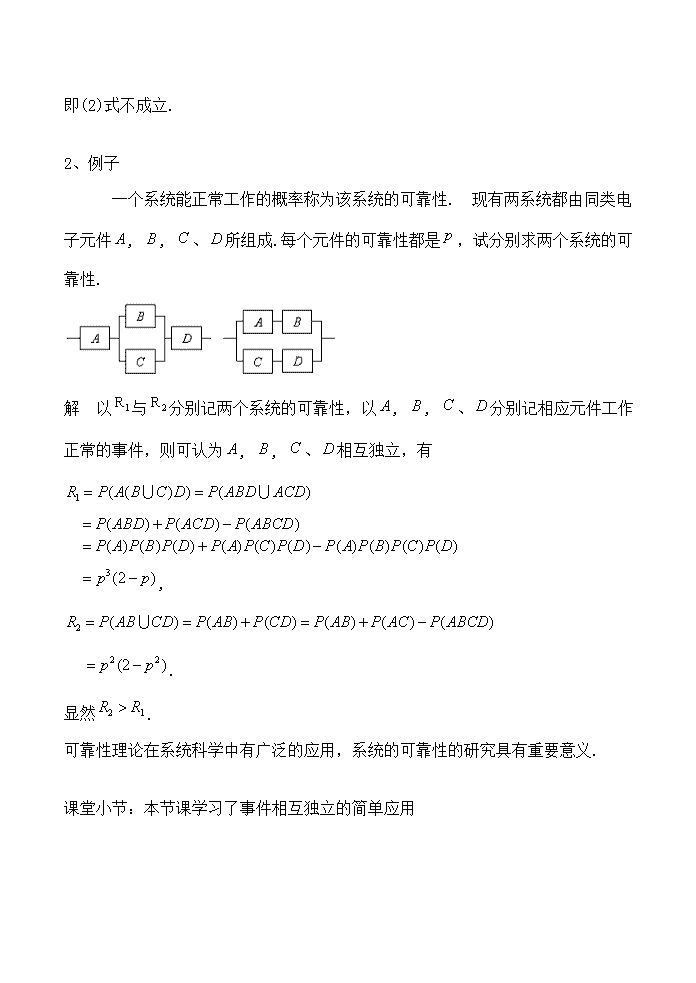高中数学独立性教案 3页

独立性教学目标：了解两个事件相互独立的概念及简单应用教学重点：了解两个事件相互独立的概念及简单应用教学过程一、复习引入：1.已知事件发生条件下事件发生的概率称为事件关于事件的条件概率，记作.2.对任意事件和，若，则“在事件发生的条件下的条件概率”，记作P(A|B)，定义为3.事件发生与否对事件发生的概率没有影响，即.称与独立二、讲解新课：1、多个事件的独立性对个事件，除考虑两两的独立性以外，还得考虑其整体的相互独立性.以三个事件,,为例.定义若\n(1)且(2)则称,,相互独立.(1)式表示,,两两独立，所以独立包含了两两独立.但,,的两两独立并不能代替三个事件相互独立，因为还有(2)式.那么(1)式是否包含(2)式呢？回答是否定的，有例如下：例一个均匀的正四面体，其第一面染成红色，第二面为白色，第三面为黑色，第四面红白黑三色都有.分别用,,记投一次四面体时底面出现红、白、黑的事件.由于在四面体中有两面出现红色，故；同理,；同时出现两色或同时出现三色只有第四面，故,因此,，，(1)式成立，,,两两独立.但,\n即(2)式不成立.2、例子一个系统能正常工作的概率称为该系统的可靠性.现有两系统都由同类电子元件,,、所组成.每个元件的可靠性都是，试分别求两个系统的可靠性.解以与分别记两个系统的可靠性，以,,、分别记相应元件工作正常的事件，则可认为,,、相互独立，有,.显然.可靠性理论在系统科学中有广泛的应用，系统的可靠性的研究具有重要意义.课堂小节：本节课学习了事件相互独立的简单应用