高中数学指数函数教案 4页

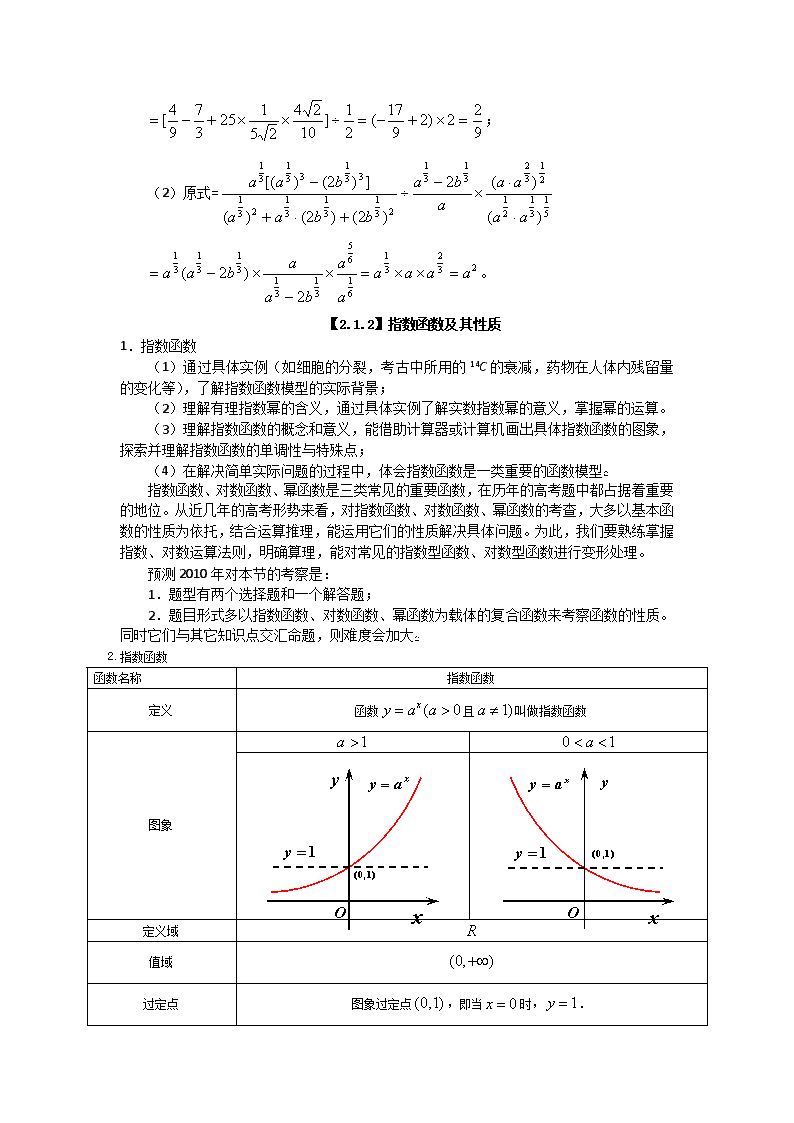
函数第二讲〖2.1〗指数函数（1）根式的概念①如果，且，那么叫做的次方根．当是奇数时，的次方根用符号表示；当是偶数时，正数的正的次方根用符号表示，负的次方根用符号表示；0的次方根是0；负数没有次方根．②式子叫做根式，这里叫做根指数，叫做被开方数．当为奇数时，为任意实数；当为偶数时，．③根式的性质：；当为奇数时，；当为偶数时，．（2）分数指数幂的概念①正数的正分数指数幂的意义是：且．0的正分数指数幂等于0．②正数的负分数指数幂的意义是：且．0的负分数指数幂没有意义．注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①②③四．【典例解析】题型1：指数运算例1．（1）计算：；（2）化简：。解：（1）原式=\n；（2）原式=。【2.1.2】指数函数及其性质1．指数函数（1）通过具体实例（如细胞的分裂，考古中所用的14C的衰减，药物在人体内残留量的变化等），了解指数函数模型的实际背景；（2）理解有理指数幂的含义，通过具体实例了解实数指数幂的意义，掌握幂的运算。（3）理解指数函数的概念和意义，能借助计算器或计算机画出具体指数函数的图象，探索并理解指数函数的单调性与特殊点；（4）在解决简单实际问题的过程中，体会指数函数是一类重要的函数模型指数函数、对数函数、幂函数是三类常见的重要函数，在历年的高考题中都占据着重要的地位。从近几年的高考形势来看，对指数函数、对数函数、幂函数的考查，大多以基本函数的性质为依托，结合运算推理，能运用它们的性质解决具体问题。为此，我们要熟练掌握指数、对数运算法则，明确算理，能对常见的指数型函数、对数型函数进行变形处理。预测2010年对本节的考察是：1．题型有两个选择题和一个解答题；2．题目形式多以指数函数、对数函数、幂函数为载体的复合函数来考察函数的性质。同时它们与其它知识点交汇命题，则难度会加大2.指数函数函数名称指数函数定义0101函数且叫做指数函数图象定义域值域过定点图象过定点，即当时，．\n奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内，越大图象越高；在第二象限内，越大图象越低．例1．（2008广东理7）设，若函数，有大于零的极值点，则（B）A．B．C．D．【解析】，若函数在上有大于零的极值点，即有正根。当有成立时,显然有,此时，由我们马上就能得到参数的范围为.题型5：指数函数的图像与应用例9．若函数的图象与x轴有公共点，则m的取值范围是（）A．m≤－1B．－1≤m<0C．m≥1D．00，即b<0.所以选D.点评：观察图象变化趋势，得到函数的单调性，结合指数函数的单调性，得到参数a的范围.根据所给函数式的平移变换规律，得到参数b的范围.也可以取x=1时的特殊点，得到，从而b<0.【例4】已知函数.（1）求该函数的图象恒过的定点坐标；（2）指出该函数的单调性.解：（1）当，即时，.所以，该函数的图象恒过定点.（2）∵是减函数，∴当时，在R上是增函数；当时，在R上是减函数.【例2】已知.（1）讨论的奇偶性；（2）讨论的单调性.解：（1）的定义域为R.∵.∴为奇函数.（2）设任意，且，则.由于，从而，即.∴，即.∴为增函数.点评：在这里，奇偶性与单调性的判别，都是直接利用知识的定义来解决.需要我们理解两个定义，掌握其运用的基本模式，并能熟练的进行代数变形，得到理想中的结果.【例3】求下列函数的单调区间：（1）；（2）.解：（1）设.由知，在上为减函数，在上为增函数.根据的单调性，当时，y关于u为增函数；当时，y关于u为减函数.∴当时，原函数的增区间为，减区间为；当时，原函数的增区间为，减区间为.（2）函数的定义域为.设.易知为减函数.而根据的图象可以得到，在区间与上，y关于u均为减函数.∴在上，原函数为增函数；在上，原函数也为增函数.