- 313.00 KB
- 2022-08-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
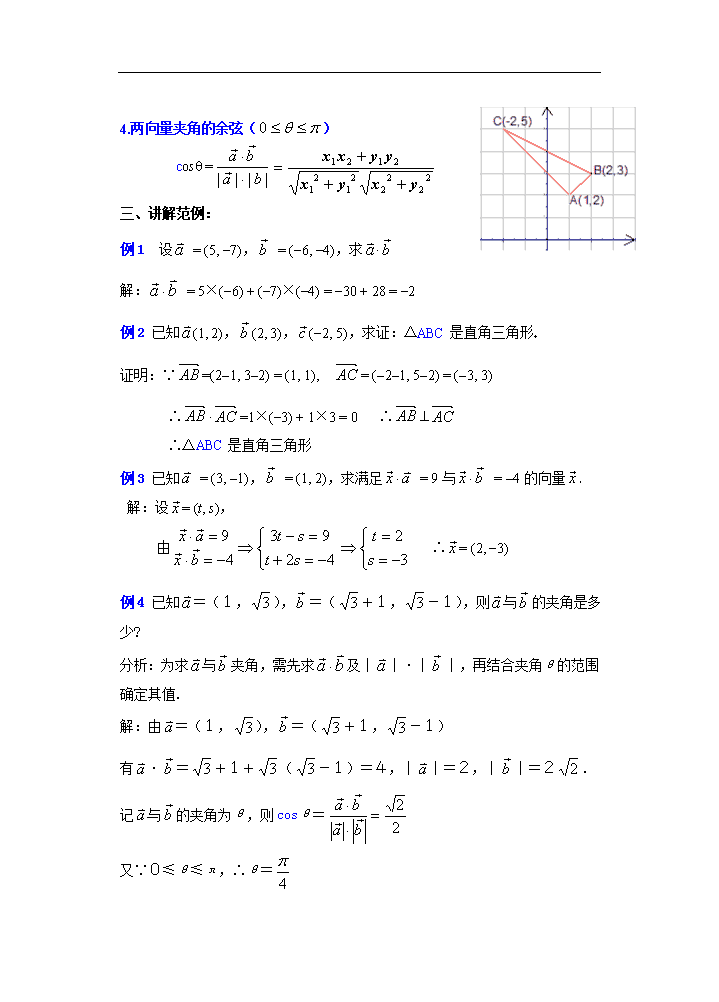
课题:平面向量数量积的坐标表示教学目的:⑴要求学生掌握平面向量数量积的坐标表示⑵掌握向量垂直的坐标表示的充要条件,及平面内两点间的距离公式⑶能用所学知识解决有关综合问题教学重点:平面向量数量积的坐标表示教学难点:平面向量数量积的坐标表示的综合运用授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:1.两个非零向量夹角的概念已知非零向量与,作=,=,则∠AOB=θ(0≤θ≤π)叫与的夹角.2.平面向量数量积(内积)的定义:已知两个非零向量与,它们的夹角是θ,则数量||||cosq叫与的数量积,记作×,即有×=||||cosq,(0≤θ≤π).并规定与任何向量的数量积为03.向量的数量积的几何意义:数量积×等于的长度与在方向上投影||cosq的乘积4.两个向量的数量积的性质:设、为两个非零向量,是与同向的单位向量1°×=×=||cosq;2°^Û×=03°当与同向时,×=||||;当与反向时,×=-||||特别的×=||2或\n4°cosq=;5°|×|≤||||5.平面向量数量积的运算律交换律:×=×数乘结合律:()×=(×)=×()分配律:(+)×=×+×二、讲解新课:⒈平面两向量数量积的坐标表示已知两个非零向量,,试用和的坐标表示设是轴上的单位向量,是轴上的单位向量,那么,所以又,,所以这就是说:两个向量的数量积等于它们对应坐标的乘积的和即2.平面内两点间的距离公式(1)设,则或(2)如果表示向量的有向线段的起点和终点的坐标分别为、,那么(平面内两点间的距离公式)3.向量垂直的判定设,,则\n4.两向量夹角的余弦()cosq=三、讲解范例:例1设=(5,-7),=(-6,-4),求×解:=5×(-6)+(-7)×(-4)=-30+28=-2例2已知(1,2),(2,3),(-2,5),求证:△ABC是直角三角形证明:∵=(2-1,3-2)=(1,1),=(-2-1,5-2)=(-3,3)∴×=1×(-3)+1×3=0∴^∴△ABC是直角三角形例3已知=(3,-1),=(1,2),求满足×=9与×=-4的向量解:设=(t,s),由∴=(2,-3)例4已知=(1,),=(+1,-1),则与的夹角是多少?分析:为求与夹角,需先求及||·||,再结合夹角θ的范围确定其值.解:由=(1,),=(+1,-1)有·=+1+(-1)=4,||=2,||=2.记与的夹角为θ,则cosθ=又∵0≤θ≤π,∴θ=\n评述:已知三角形函数值求角时,应注重角的范围的确定.例5如图,以原点和A(5,2)为顶点作等腰直角△ABC,使Ð=90°,求点和向量的坐标解:设点坐标(x,y),则=(x,y),=(x-5,y-2)∵^∴x(x-5)+y(y-2)=0即:x2+y2-5x-2y=0又∵||=||∴x2+y2=(x-5)2+(y-2)2即:10x+4y=29由∴点坐标或;=或例6在△ABC中,=(2,3),=(1,k),且△ABC的一个内角为直角,求k值解:当=90°时,×=0,∴2×1+3×k=0∴k=当=90°时,×=0,=-=(1-2,k-3)=(-1,k-3)∴2×(-1)+3×(k-3)=0∴k=当C=90°时,×=0,∴-1+k(k-3)=0∴k=四、课堂练习:1.若=(-4,3),=(5,6),则3||2-4=()A.23B.57C.63D.832.已知(1,2),(2,3),(-2,5),则△为()A.直角三角形B.锐角三角形C.钝角三角形D.不等边三角形3.已知=(4,3),向量是垂直的单位向量,则等于()\nA.或B.或C.或D.或4.=(2,3),=(-2,4),则(+)·(-)=.5.已知(3,2),(-1,-1),若点P(x,-)在线段的中垂线上,则x=.6.已知(1,0),(3,1),(2,0),且=,=,则与的夹角为.参考答案:1.D2.A3.D4.–75.6.45°五、小结两向量数量积的坐标表示长度、夹角、垂直的坐标表示六、课后作业:1.已知=(2,3),=(-4,7),则在方向上的投影为()A.B.C.D.2.已知=(λ,2),=(-3,5)且与的夹角为钝角,则λ的取值范围是()A.λ>B.λ≥C.λ<D.λ≤3.给定两个向量=(3,4),=(2,-1)且(+x)⊥(-),则x等于()A.23B.C.D.4.已知||=,=(1,2)且∥,则的坐标为.5.已知=(1,2),(1,1),=-k,若⊥,则=.6.已知=(3,0),=(k,5)且与的夹角为,则k的值为.7.已知=(3,-1),=(1,2),求满足条件x·=9与x·=-4的向量x.8.已知点A(1,2)和B(4,-1),问能否在y轴上找到一点C,使∠ABC=90°,若不能,说明理由;若能,求C点坐标.\n9.四边形ABCD中=(6,1),=(x,y),=(-2,-3),(1)若∥,求x与y间的关系式;(2)满足(1)问的同时又有⊥,求x,y的值及四边形ABCD的面积.参考答案:1.C2.A3.C4.(,2)或(-,-2)5.()6.-57.(2,-3)8.不能(理由略)9.(1)x+2y=0(2)S四边形ABCD=16七、板书设计(略)八、课后记及备用资料:已知=(3,4),=(4,3),求x,y的值使(x+y)⊥,且|x+y|=1.分析:这里两个条件互相制约,注意体现方程组思想.解:由=(3,4),=(4,3),有x+y=(3x+4y,4x+3y)又(x+y)⊥(x+y)·=03(3x+4y)+4(4x+3y)=0即25x+24y=0①又|x+y|=1|x+y|2=1(3x+4y)2+(4x+3y)2=1整理得:25x2+48xy+25y2=1即x(25x+24y)+24xy+25y2=1②由①②有24xy+25y2=1③将①变形代入③可得:y=±再代回①得: