高中数学 幂函数教案 湘教版 4页

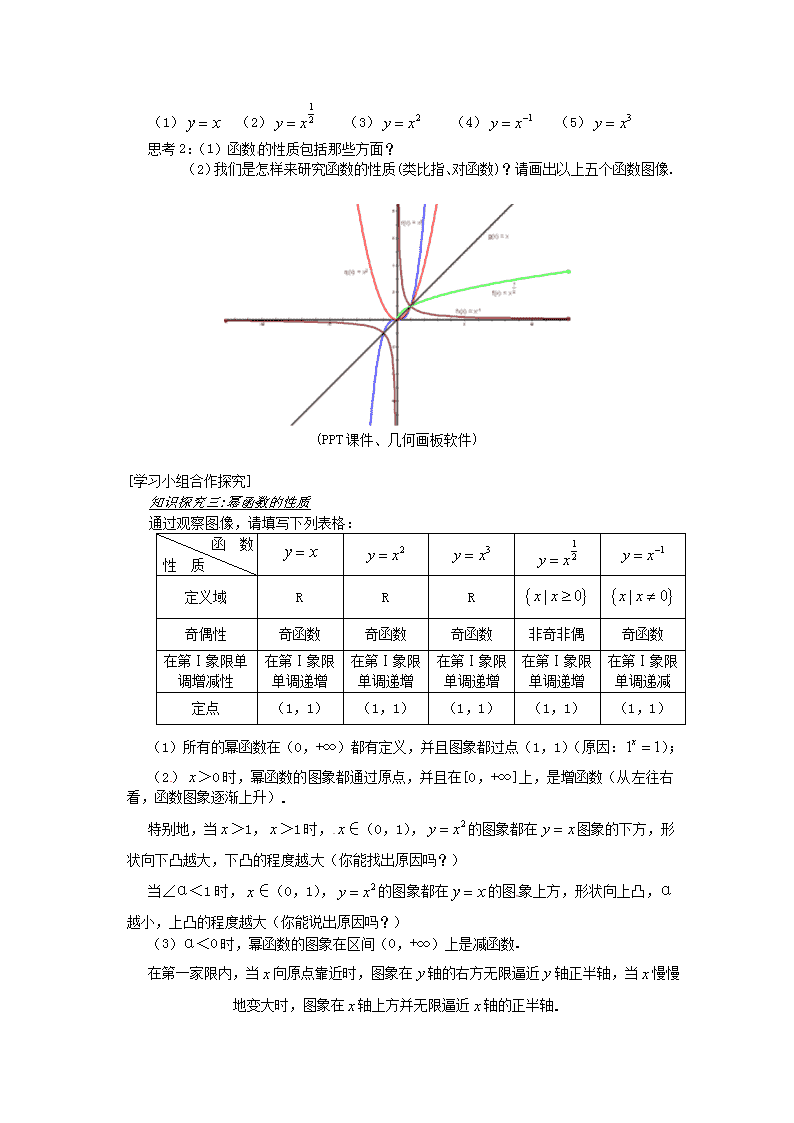
湖南省益阳市南县第一中学2013-2014学年高中数学幂函数教案湘教版教学目标：1．知识技能（1）理解幂函数的概念；（2）通过具体实例了解幂函数的图象和性质，并能进行初步的应用.2．过程与方法类比研究一般函数，指数函数、对数函数的过程与方法，后研幂函数的图象和性质.3．情感、态度、价值观（1）进一步渗透数形结合与类比的思想方法；（2）体会幂函数的变化规律及蕴含其中的对称性.重点、难点重点：从五个具体的幂函数中认识的概念和性质难点：从幂函数的图象中概括其性质学法与教学用具（1）学法：通过自主学习、合作交流、深入探究等教学设计，理解幂函数的定义和性质;（2）教学用具：多媒体辅助教学（PPT课件、几何画板软件）一、自主学习：通读教材教学过程：二、情景导入阅读教材P77的具体实例（1）~（5），思考下列问题.（1）它们的对应法则分别是什么？（2）以上问题中的函数有什么共同特征？答：(1)(2)三、探究新知知识探究一：幂函数的概念一般地，形如（R）的函数称为幂函数，其中是自变量，是常数.如等都是幂函数，幂函数与指数函数，对数函数一样，都是基本初等函数.【问题1】下列函数中，是幂函数为:①y=;②y=;③y=④y=-;⑤y=;⑥y=;⑦y=+思考1:幂函数和指数函数有什么相同点和区别?知识探究二::幂函数的图象[学生自主探究]研究下列五个函数\n（1）（2）（3）（4）（5）思考2：（1）函数的性质包括那些方面？（2）我们是怎样来研究函数的性质(类比指、对函数)？请画出以上五个函数图像.(PPT课件、几何画板软件)[学习小组合作探究]知识探究三:幂函数的性质通过观察图像，请填写下列表格：函数性质定义域RRR奇偶性奇函数奇函数奇函数非奇非偶奇函数在第Ⅰ象限单调增减性在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减定点（1，1）（1，1）（1，1）（1，1）（1，1）（1）所有的幂函数在（0，+∞）都有定义，并且图象都过点（1，1）（原因：）；（2）＞0时，幂函数的图象都通过原点，并且在[0，+∞]上，是增函数（从左往右看，函数图象逐渐上升）.特别地，当＞1，＞1时，∈（0，1），的图象都在图象的下方，形状向下凸越大，下凸的程度越大（你能找出原因吗？）当∠α＜1时，∈（0，1），的图象都在的图象上方，形状向上凸，α越小，上凸的程度越大（你能说出原因吗？）（3）α＜0时，幂函数的图象在区间（0，+∞）上是减函数.在第一家限内，当向原点靠近时，图象在轴的右方无限逼近轴正半轴，当慢慢地变大时，图象在轴上方并无限逼近轴的正半轴.[\n知识迁移与运用：【问题2】证明幂函数上是增函数证明：任取＜则==因＜0，＞0所以，即上是增函数.思考：我们知道，若得，你能否用这种作比的方法来证明上是增函数，利用这种方法需要注意些什么？【问题3】利用函数的性质，判断下列各组数的大小1.10.4,1.20.4；0.24-0.6,0.25-0.6；四．反馈练习：（1）设函数，当m=________时，为幂函数。（2）画出的大致图象，并求出其定义域、奇偶性，并判断和证明其单调性.（3）比较下列各组数的大小：①和②和③和④、和⑤和五．归纳小结：（1）我们今天学习了哪一类基本函数，它们定义是怎样描述的？（2）你能根据函数图象说出有关幂函数的性质吗？\n作业：P79习题2.3第2、3题