高中数学算法案例(全套)教案苏教版必修3 教案 12页

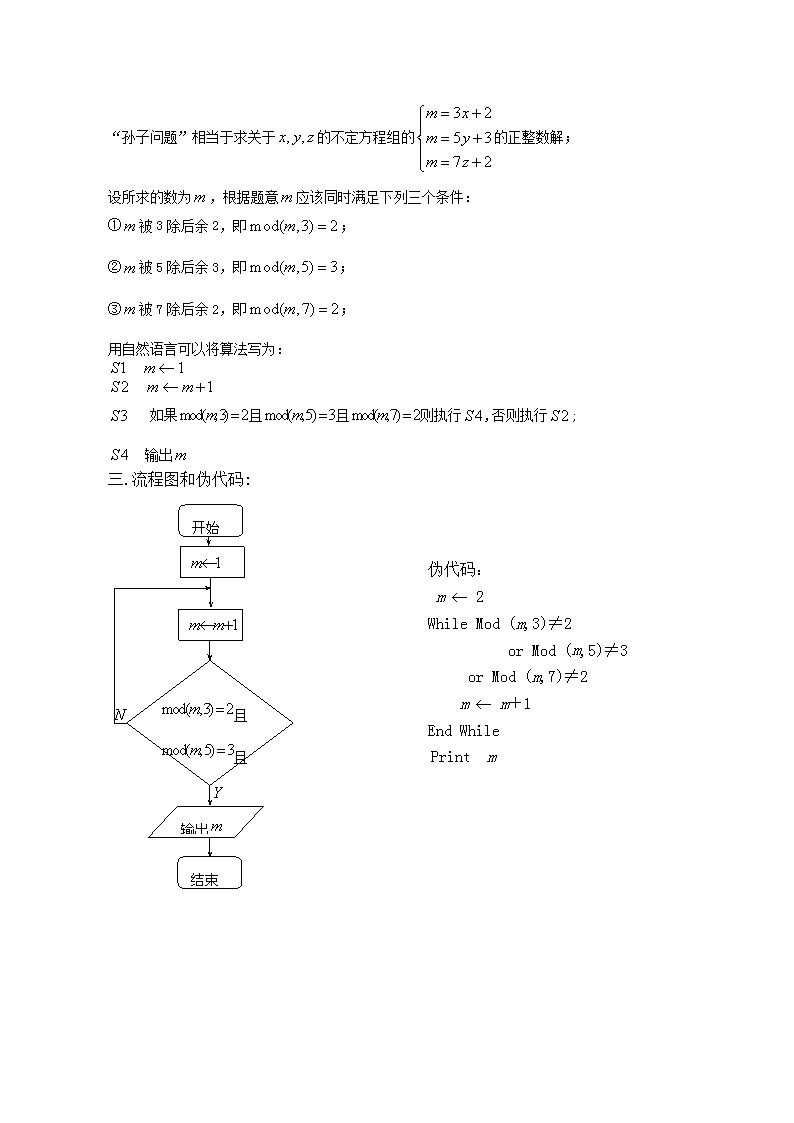
§1.4算法案例(1)教学目标：（1）介绍中国古代算法的案例－韩信点兵－孙子问题；（2）用三种方法熟练的表示一个算法；（3）让学生感受算法的意义和价值．教学重点、难点:不定方程解法的算法．教学过程：一、问题情境(韩信点兵-孙子问题)：韩信是秦末汉初的著名军事家。据说有一次汉高祖刘邦在卫士的簇拥下来到练兵场，刘邦问韩信有什么方法，不要逐个报数，就能知道场上的士兵的人数。韩信先令士兵排成3列纵队，结果有2个人多余；接着立即下令将队形改为5列纵队，这一改，又多出3人；随后他又下令改为7列纵队，这次又剩下2人无法成整行。在场的人都哈哈大笑，以为韩信不能清点出准确的人数，不料笑声刚落，韩信高声报告共有士兵2333人。众人听了一愣，不知道韩信用什么方法这么快就能得出正确的结果的。同学们，你知道吗？背景说明:1．类似的问题最早出现在我国的《算经十书》之一的《孙子算经》中原文是：“今有物，不知其数，三三数之，剩二，五五数之，剩三，七七数之，剩二，问物几何？答曰：「二十三」”2．孙子算经的作者及确实着作年代均不可考，不过根据考证，着作年代不会在晋朝之後，以这个考证来说上面这种问题的解法，中国人发现得比西方早，所以这个问题的推广及其解法，被称为中国剩余定理(孙子定理)。中国剩余定理在近代抽象代数学中占有一席非常重要的地位；3．该问题的完整的表述，后来经过宋朝数学家秦九韶的推广，又发现了一种算法，叫做“大衍求一术”。在中国还流传着这么一首歌诀：三人同行七十稀，五树梅花廿一枝，七子团圆月正半，除百零五便得知。它的意思是说：将某数（正整数）除以3所得的余数乘以70，除以5所得的余数乘以21，除以7所得的余数乘以15，再将所得的三个积相加，并逐次减去105，减到差小于105为止。所得结果就是某数的最小正整数值。用上面的歌诀来算《孙子算经》中的问题，便得到算式：2×70+3×21+2×15=233，233－105×2=23，即所求物品最少是23件。二.算法设计思想:\n“孙子问题”相当于求关于的不定方程组的的正整数解；设所求的数为，根据题意应该同时满足下列三个条件：①被3除后余2，即；②被5除后余3，即；③被7除后余2，即；用自然语言可以将算法写为：如果且且则执行,否则执行;输出三.流程图和伪代码:输出且且开始结束伪代码：m¬2WhileMod(m,3)≠2orMod(m,5)≠3orMod(m,7)≠2m¬m＋1EndWhilePrintm\n练习:有3个连续的自然数，其中最小的能被15整除，中间的能被17整除，最大的能被19整除，求满足要求的一组三个连续的自然数。伪代码：m¬2WhileMod(m,15)=0orMod(m+1,17)=0orMod(m+2,19)=0m¬m＋1EndWhilePrintm,m+1,m+2思考：以下伪代码是否可行？k¬1a¬15kWhileMod(a＋1,17)≠0or_Mod(a＋2,19)≠0k¬k＋1a¬15kEndWhilePrinta,a＋1,a＋2四、回顾小结：1．中国数学在世界数学史上的巨大贡献,韩信点兵－孙子问题的求解算法；2．利用循环结构实现整数的搜索；3．利用逻辑运算符Or和And实现多条件的判断。五【随堂演练】：1.下列各数中,被3,5,9除都余2的正整数是(A)A.17B.47C.29D.11\n2．有一堆火柴棒，三根三根的数，最后余下两根；五根无根的数，最后余下三根；七根七根的数，最后余下两根。那么这对火柴棒最少是__23________根.3.4.有一把围棋子,5个5个地数,最后余下2个;7个7个地数,最后余下3个;9个9个地数,最后余下4个.请设计一种算法,求出这把棋子至少有多少个.伪代码：m¬2WhileMod(m,3)≠2orMod(m,7)≠3orMod(m,9)≠4m¬m＋1EndWhilePrintm§1.4算法案例(2)教学目标：（1）理解辗转相除法与更相减损术中蕴含的数学原理，并能根据这些原理进行算法分析；（2）基本能根据算法语句与程序框图的知识设计完整的程序框图并写出算法程序；教学重点：理解辗转相除法与更相减损术求最大公约数的方法教学难点：把辗转相除法与更相减损术的方法转换成程序框图与程序语言．教学过程：一、问题情境在初中，我们已经学过求最大公约数的知识，你能求出18与30的公约数吗？\n我们都是利用找公约数的方法来求最大公约数，如果公约数比较大而且根据我们的观察又不能得到一些公约数，我们又应该怎样求它们的最大公约数？比如求8251与6105的最大公约数？这就是我们这一堂课所要探讨的内容．二、算法设计思想：1.辗转相除法：例1．求两个正数8251和6105的最大公约数．（分析：8251与6105两数都比较大，而且没有明显的公约数，如能把它们都变小一点，根据已有的知识即可求出最大公约数）解：8251＝6105×1＋2146显然8251和的2146最大公约数也必是2146的约数，同样6105与2146的公约数也必是8251的约数，所以8251与6105的最大公约数也是6105与2146的最大公约数．6105＝2146×2＋18132146＝1813×1＋3331813＝333×5＋148333＝148×2＋37148＝37×4＋0则37为8251与6105的最大公约数．以上我们求最大公约数的方法就是辗转相除法．也叫欧几里德算法，它是由欧几里德在公元前300年左右首先提出的．利用辗转相除法求最大公约数的步骤如下：第一步：用较大的数除以较小的数得到一个商和一个余数；第二步：若，则为的最大公约数；若，则用除数除以余数得到一个商和一个余数；第三步：若，则为的最大公约数；若，则用除数除以余数得到一个商和一个余数；……依次计算直至，此时所得到的即为所求的最大公约数．练习：利用辗转相除法求两数4081与20723的最大公约数（答案：53）2.更相减损术我国早期也有解决求最大公约数问题的算法，就是更相减损术．更相减损术求最大公约数的步骤如下：可半者半之，不可半者，副置分母之数，以少减多，更相减损，求其等也，以等数约之．翻译出来为：第一步：任意给出两个正数；判断它们是否都是偶数．若是，用2约简；若不是，执行第二步．\n第二步：以较大的数减去较小的数，接着把较小的数与所得的差比较，并以大数减小数．继续这个操作，直到所得的数相等为止，则这个数（等数）就是所求的最大公约数．例2．用更相减损术求98与63的最大公约数.解：由于63不是偶数，把98和63以大数减小数，并辗转相减，即：98－63＝3563－35＝2835－28＝728－7＝2121－7＝1414－7＝7所以，98与63的最大公约数是7．练习：用更相减损术求两个正数84与72的最大公约数．（答案：12）3.比较辗转相除法与更相减损术的区别（1）都是求最大公约数的方法，计算上辗转相除法以除法为主，更相减损术以减法为主，计算次数上辗转相除法计算次数相对较少，特别当两个数字大小区别较大时计算次数的区别较明显．（2）从结果体现形式来看，辗转相除法体现结果是以相除余数为0则得到，而更相减损术则以减数与差相等而得到．三．辗转相除法的流程图及伪代码（1）算理：所谓辗转相除法，就是对于给定的两个数，用较大的数除以较小的数。若余数不为零，则将余数和较小的数构成新的一对数，继续上面的除法，直到大数被小数除尽，则这时较小的数就是原来两个数的最大公约数。（2）算法步骤第一步：输入两个正整数m,n(m>n).第二步：计算a除以b所得的余数r.第三步：a=b,b=r.第四步：若r＝0,则a,b的最大公约数等于b；否则转到第二步.第五步：输出最大公约数b.（3）辗转相除法的程序框图及程序程序框图：\n输出b开始输入a,b结束伪代码:用较大的数除以较小的数，得到除式，直到.例1试画出求两个正整数a,b最小公倍数的流程图，并写出其伪代码。三个正整数？伪代码:Reada,bc¬abWhileMod(a,b)≠0r¬Mod(a,b)a¬b\nb¬rEndWhilePrintc/b2.更相减损术（1）算理：所谓更相减损术，就是对于给定的两个数，用较大的数减去较小的数，然后将差和较小的数构成新的一对数，再用较大的数减去较小的数，反复执行此步骤直到差数和较小的数相等，此时相等的两数便为原来两个数的最大公约数。（2）算法步骤第一步：输入两个正整数a,b(a>b);第二步：若a不等于b,则执行第三步；否则转到第五步；第三步：把a-b的差赋予r;第四步：如果b>r,那么把b赋给a,把r赋给b;否则把r赋给a，执行第二步；第五步：输出最大公约数b.程序框图：伪代码:Reada,bWhilea=br¬a-bIfb>rThena¬bb¬rElsea¬rEndIfEndWhilePrintbEnd3.比较辗转相除法与更相减损术的区别（1）都是求最大公约数的方法，计算上辗转相除法以除法为主，更相减损术以减法为主，计算次数上辗转相除法计算次数相对较少，特别当两个数字大小区别较大时计算次数的区别较明显．\n（2）从结果体现形式来看，辗转相除法体现结果是以相除余数为0则得到，而更相减损术则以减数与差相等而得到．四、回顾小结：比较辗转相除法与更相减损术的区别（1）都是求最大公约数的方法，计算上辗转相除法以除法为主，更相减损术以减法为主，计算次数上辗转相除法计算次数相对较少，特别当两个数字大小区别较大时计算次数的区别较明显。（2）从结果体现形式来看，辗转相除法体现结果是以相除余数为0则得到，而更相减损术则以减数与差相等而得到五【随堂演练】1.整数143和65的最大公约数为(A)A.13B.11C.5D.92.如果是整数,且,则与的最大公约数为(D)A.B.C.D.与的最大公约数3.用辗转相除法求85和51的最大公约数时,需要做除法的次数为__3________4分别用辗转相除法和更相减损法求91和49的最大公约数.5.91=49×1+4291-49=4249=42×1＋749-42=742=7×642-7=35∴(91,49)=735-7=28(91,49)=(42,49)=(7,49)=728-7=2121-7=1414-7=7\n6.根据更相减损法的思想，设计求两个整数的最小公倍数的算法过程，并画出流程图，写出伪代码。§1.4算法案例(3)教学目标：（1）二分法主要是采用了循环结构处理问题要会分析类似的问题；（2）GoTo语句的认识及其他语句的进一步熟悉；（3）能由流程图分析出期所含有的结构并用为代码表示出相应的算法．教学重点：二分法的算法思想和算法表示．教学过程：一、问题情境：必修1中我们学习了二分法求方程的近似解，大家还能想起二分法的求解步骤吗？二、案例讲解：案例：写出用区间二分法求解方程在区间内的一个近似解（误差不超过0.001）的一个算法．（１）算法设计思想：如图，如果估计出方程在某区间内有一个根，就能用二分法搜索求得符合误差限制的近似解．\n（２）算法步骤可以表示为：　　取的中点，间区间一分为二；　　若，则就是方程的根，否则判断根在的左侧还是后侧；若，则，以代替；若，则，以代替；　　若，计算终止，此时，否则转．（３）流程图：（4）伪代码1：结束开始Reada，b，cWhileAndIf<0ThenElseEndIfEndWhilePrint\n伪代码2：10Read20304050IfThenGoTo12060IfThen7080Else90100EndIf110IfThenGoTo20120Print二分搜索的过程是一个多次重复的过程，故可以用循环结构来处理（代码1），课本解法是采用语句实现的（代码2）。三、回顾小结：1．二分法的算法和用伪代码表示该算法；2．语句的使用；3．解决实际问题的过程：分析－画流程图－写伪代码。四、课外作业：课本复习题的第1题,课本复习题的第10题补充．一个三位数的十位和个位的数字互换，得到的一个新的三位数，新、旧两个三位数都能被4整除；设计一个算法，求满足条件的三位数的个数，并写出伪代码。