高中数学(指数函数)教案2 苏教版必修1 教案 8页

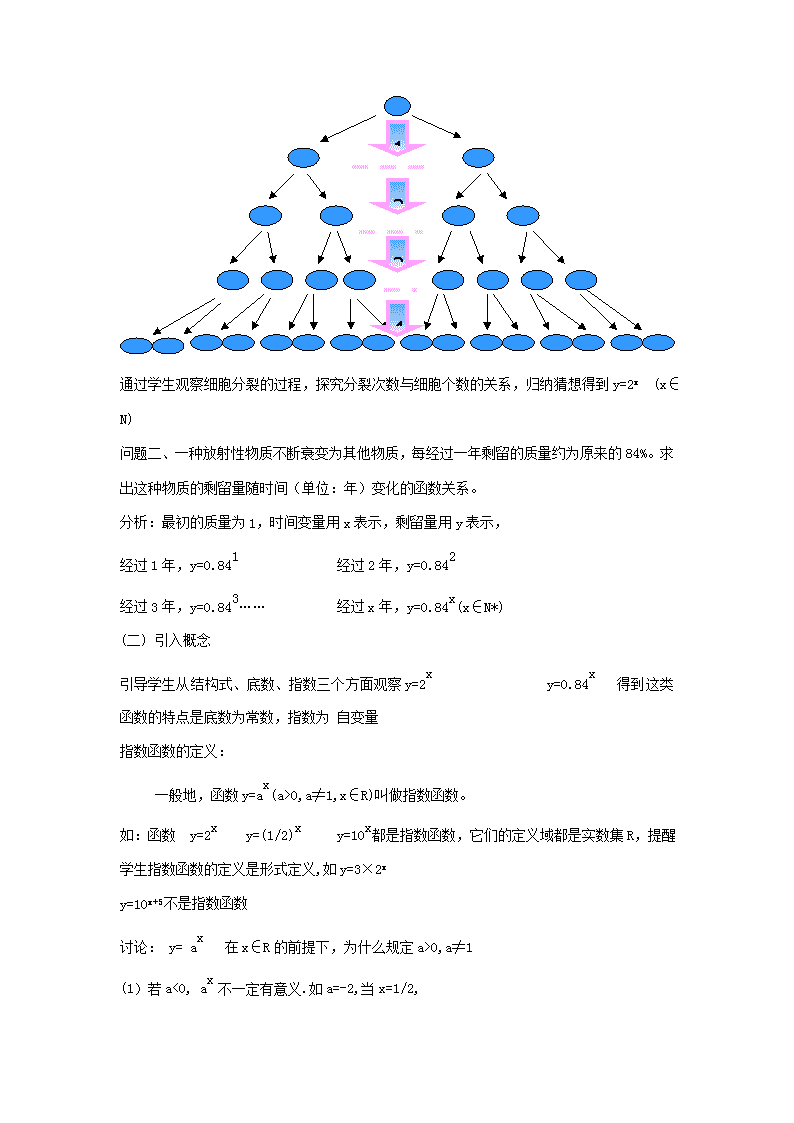
指数函数一、教学目标1、知识与技能：了解指数函数模型的实际背景，掌握指数函数的概念和意义，掌握指数函数的图象和性质。2、过程与方法：通过对指数函数的概念图象性质的学习,培养学生观察、分析、归纳猜想的能力,进一步体会数形结合的思想方法.3、情感、态度和价值观：通过对指数函数的研究,让学生体验从特殊到一般的学习规律，认识数学的应用价值,激发学生学习数学的兴趣，培养学生的创新意识。二、教学重点、难点重点：指数函数的图像和性质。难点：指数函数的图象性质与底数a的关系。突破难点的关键：寻找新知识生长点，建立新旧知识的联系，在理解概念的基础上充分结合图象，利用数形结合来扫清障碍。三、教学方法与手段本节课采用自主探究、合作交流的教学方法，借助多媒体，引导学生观察、分析、归纳、概括，调动学生参与课堂教学的主动性和积极性。四、教学过程(一)创设情境问题一、某种细胞分裂时，每次每个细胞分裂为2个，则1个这样的细胞第一次分裂后变为细胞2个，第2次分裂后就得到4个细胞，第3次分裂后就得到8个细胞，……分裂次数x与细胞个数y有什么关系\n1234通过学生观察细胞分裂的过程，探究分裂次数与细胞个数的关系，归纳猜想得到y=2x(x∈N)问题二、一种放射性物质不断衰变为其他物质，每经过一年剩留的质量约为原来的84%。求出这种物质的剩留量随时间（单位：年）变化的函数关系。分析：最初的质量为1，时间变量用x表示，剩留量用y表示，经过1年，y=0.841经过2年，y=0.842经过3年，y=0.843……经过x年，y=0.84x(x∈N*)(二)引入概念引导学生从结构式、底数、指数三个方面观察y=2xy=0.84x得到这类函数的特点是底数为常数，指数为自变量指数函数的定义：一般地，函数y=ax(a>0,a≠1,x∈R)叫做指数函数。如：函数y=2xy=(1/2)xy=10x都是指数函数，它们的定义域都是实数集R，提醒学生指数函数的定义是形式定义,如y=3×2xy=10x+5不是指数函数讨论：y=ax在x∈R的前提下，为什么规定a>0,a≠1(1）若a<0,ax不一定有意义.如a=-2,当x=1/2,\n（1）若a=0,则当x>0时，ax=0;x≤0时，ax无意义.(3)若a=1,则对于任意x∈R,ax=1为常量。练习若函数y=(a2-3a+3).ax是指数函数,则a=2（三）、图像与性质1、作出函数y=2x,y=(1/2)x的图象列出x、y的对应值表x…-3-2-10123…2x…1248…(1/2)x…8421…指导学生做出y=2xy=(1/2)x的图象观察两个函数图像的特点，借助几何画板直观展示底数不同的指数函数的图像，让学生观察底数的变化对于图像的影响。2、图像与性质01\n图象o1xyxyo1图像特征图像分布在一、二象限，在x轴的上方，过点（0，1）当x逐渐增大时，曲线从x轴的上方逐渐逼近轴当x逐渐减小时，曲线从x轴的上方逐渐逼近轴性质定义域R值域：（0，+∞）单调性在R上是减函数在R上是增函数函数值的变化规律当x=0时，y=1x<0时，y>1，x>0时，00时，y>1;3、指数函数性质的口诀：指数函数象束花，（0,1)这点把它扎，撇增捺减无例外，底互倒数纵轴夹，X=1为判底线，交点Y标看小大重视数形结合法，横轴上面图象察。4、练习（1）指数函数y=axy=bxy=cxy=dx的图象如下图所示，则底数a、b、c、d与正整数1共五个数，从大到小的顺序是b0,a≠1）的图像恒过定点(2009,2009)3、已知函数F(x)=ax(00，则00（3）若f(x1)>f(x2)，则x10.8b比较a、b的大小\n解：函数y=(0.8)x在实数集上是减函数。因为0.8a>0.8b所以a0，a≠1）比较m、n的大小答案：(1)mn;当a>1时，m解：原不等式可转化为23x+1>2-2因为y=2x在实数集上为增函数所以3x+1>-2解得x>-1所以，满足条件的取值集合是练习求满足下列条件的x值（1）4x＞23-2x（2）(五)总结巩固：1、指数函数的概念2、指数函数的图像与性质3、数学思想和方法（六）思考：1、比较a2x+1与ax+2（a>0且a≠1）的大小2、A先生从今天开始每天给你10万元，而你第一天给A先生1元，第二天给A先生2元，第三天给4元，第四天给8元……依此类推。（1）A先生要与你签订15天的合同，你同意吗？（2）A先生要与你签订30天的合同，你同意吗？五板书设计\n指数函数一、指数函数的定义二、图像与性质三、例题