高中数学 第2章(数列)教案 苏教版必修5 教案 4页

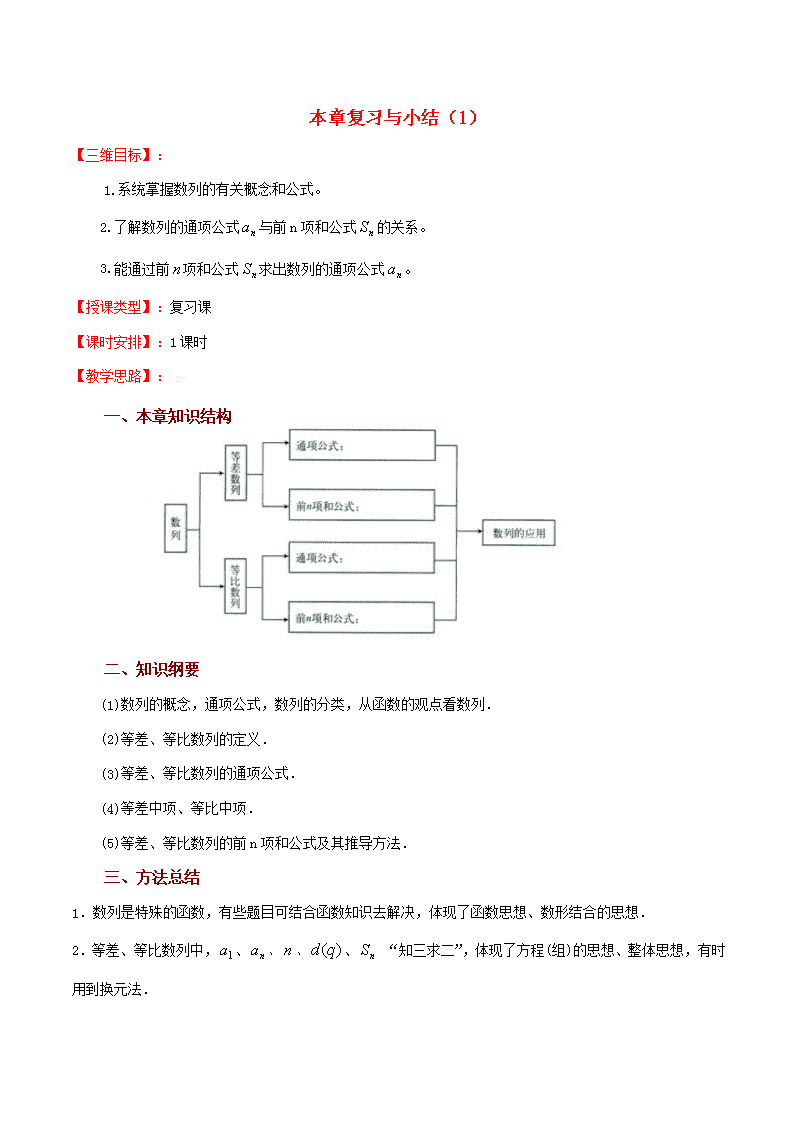
本章复习与小结（1）【三维目标】：1.系统掌握数列的有关概念和公式。2.了解数列的通项公式与前n项和公式的关系。3.能通过前项和公式求出数列的通项公式。【授课类型】：复习课【课时安排】：1课时【教学思路】：一、本章知识结构二、知识纲要(1)数列的概念，通项公式，数列的分类，从函数的观点看数列．(2)等差、等比数列的定义．(3)等差、等比数列的通项公式．(4)等差中项、等比中项．(5)等差、等比数列的前n项和公式及其推导方法．三、方法总结1．数列是特殊的函数，有些题目可结合函数知识去解决，体现了函数思想、数形结合的思想．2．等差、等比数列中，、、、、“知三求二”，体现了方程(组)的思想、整体思想，有时用到换元法．\n3．求等比数列的前项和时要考虑公比是否等于1，公比是字母时要进行讨论，体现了分类讨论的思想．4．数列求和的基本方法有：公式法，倒序相加法，错位相减法，拆项法，裂项法，累加法，等价转化等．四、知识内容：1.数列数列的通项公式：数列的前n项和：2.等差数列等差数列的定义：如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，公差通常用字母表示。等差数列的判定方法:（1）定义法：对于数列，若(常数)，则数列是等差数列。（2）等差中项：对于数列，若，则数列是等差数列。等差数列的通项公式：如果等差数列的首项是，公差是，则等差数列的通项为。说明：该公式整理后是关于的一次函数。等差数列的前项和：①②说明：对于公式②整理后是关于的没有常数项的二次函数。等差中项：如果，，成等差数列，那么叫做与的等差中项。即：或说明：在一个等差数列中，从第2项起，每一项（有穷等差数列的末项除外）都是它的前一项与后一项的等差中项；事实上等差数列中某一项是与其等距离的前后两项的等差中项。等差数列的性质：（1）等差数列任意两项间的关系：如果是等差数列的第项，是等差数列的第项，且，公差为，则有（2）对于等差数列，若，则。\n也就是：，如图所示：（3）若数列是等差数列，是其前n项的和，，那么，，成等差数列。如下图所示：3.等比数列等比数列的概念：如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列，这个常数叫做等比数列的公比，公比通常用字母表示（）。等比中项：如果在与之间插入一个数，使，，成等比数列，那么叫做与的等比中项。也就是，如果是的等比中项，那么，即。等比数列的判定方法：（1）定义法：对于数列，若，则数列是等比数列。（2）等比中项：对于数列，若，则数列是等比数列。等比数列的通项公式：如果等比数列的首项是，公比是，则等比数列的通项为。等比数列的前n项和：当时，等比数列的性质：①等比数列任意两项间的关系：如果是等比数列的第项，是等差数列的第项，且，公比为，则有②对于等比数列，若，则\n也就是：。如图所示：③若数列是等比数列，是其前n项的和，，那么，，成等比数列。如下图所示：4.数列前n项和（1）重要公式：；； （2）等差数列中，（3）等比数列中，（4）裂项求和：；（）