【教案】高中数学空间向量求距离教案人教新课标 4页

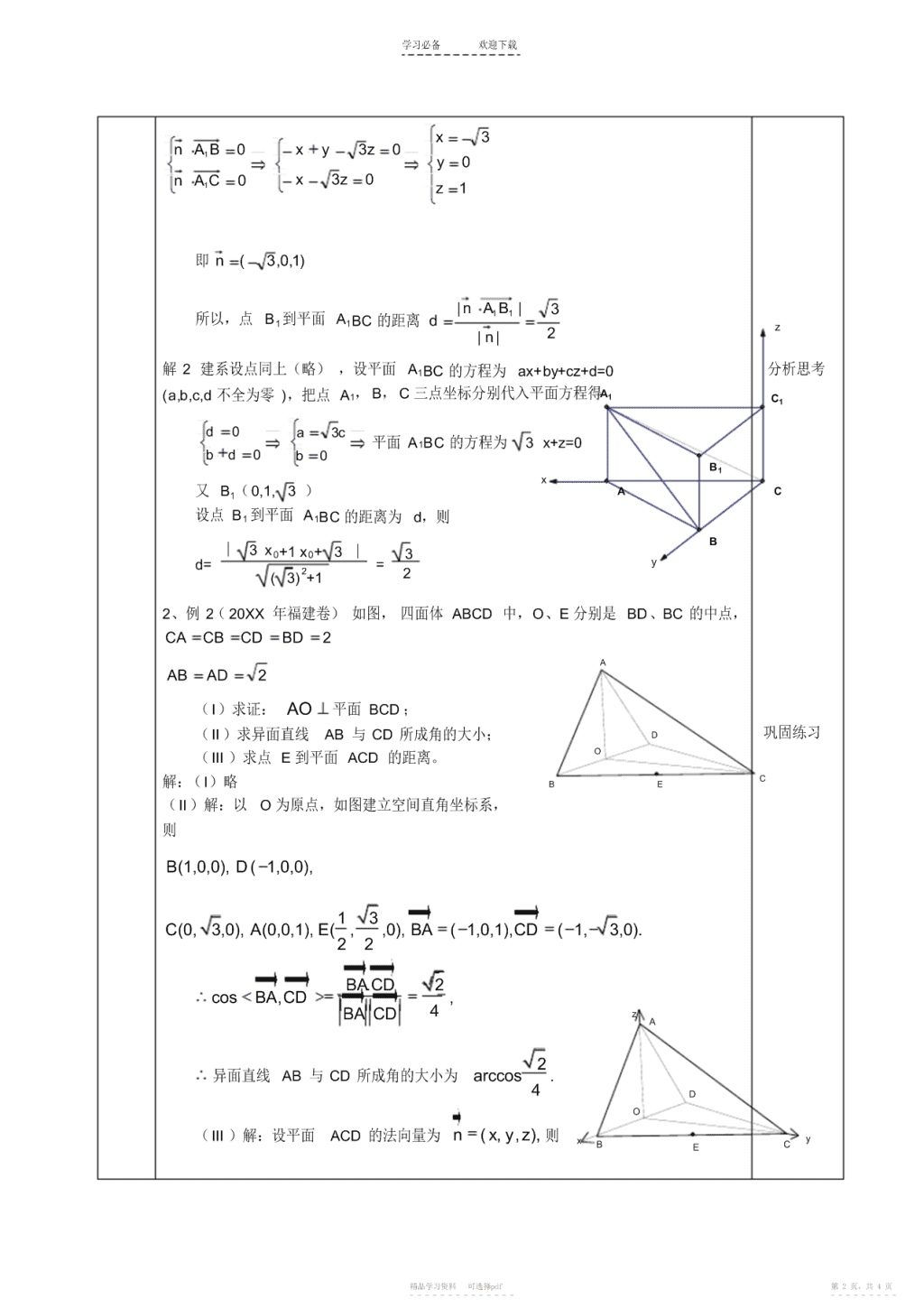
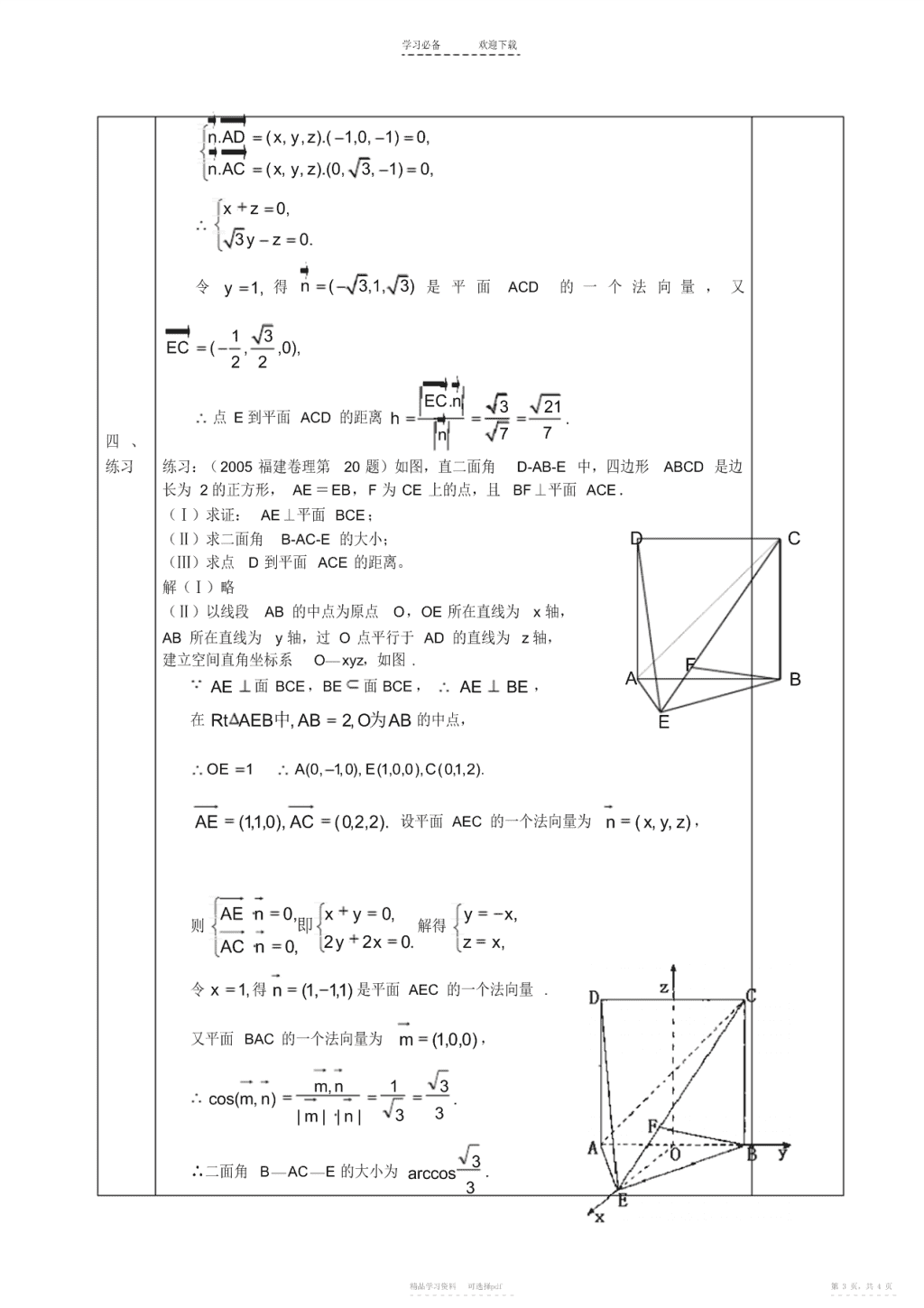
学习必备欢迎下载课题：空间的距离第一课时教学目标：知识与技能：能用向量方法进行有关距离的计算。过程与方法：分组合作，示范交流，应用小结。情感态度与价值观：掌握空间向量的应用。教学教师活动学生活动环节一、1、空间中的距离包括：两点间的距离，点到直线的距离，点到平面的距离，平行复习直线间的距离，异面直线直线间的距离，直线与平面的距离，两个平行平面间的距思考引入离。这些距离的定义各不相同，但都是转化为平面上两点间的距离来计算的。2、距离的特征：⑴距离是指相应线段的长度；⑵此线段是所有相关线段中最短的；⑶除两点间的距离外，其余总与垂直相联系。练习3、求空间中的距离有⑴直接法，即直接求出垂线段的长度；⑵转化法，转化为线面距或面面距，或转化为某三棱锥的高，由等积法或等面积法求解；⑶向量法求解。二、建构数学1、两点间的距离公式思考二、222设空间两点Axyz1,1,1,Bx2,yz2,2，则dABx1x2y1y2z1z2新课导入2、向量法在求异面直线间的距离设分别以这两异面直线上任意两点为起点和终点的向量为a，与这两条异面直线都垂直的向量为n，则两异面直线间的距离是a在n方向上的正射影向量的模。小结|an|d|n|4、向量法在求点到平面的距离中（1）设分别以平面外一点P与平面内一点M为起点和终点的向量为a，平面的法|an|向量为n，则P到平面的距离d等于a在n方向上正射影向量的模。d|n|（2）先求出平面的方程，然后用点到平面的距离公式：点P（x0,y0,z0）到平面︱Ax0+By0+Cz0+D︱AX+BY+CZ+D=0的距离d为：d=222A+B+C三、例1直三棱柱ABC-A1B1C1的侧棱AA1=3，底面ΔABC中，∠C=90°，AC=BC=1，例题分析例题求点B1到平面A1BC的距离。讲解解1：如图建立空间直角坐标系，由已知得直棱柱各顶点坐标如下：A（1,0,0），B（0,1,0），C（0,0,0）A1（1,0,3），B1（0,1,3），C1（0,0,3）∴A1B=（－1,1,－3），A1C=（－1,0,－3）B1A1=（1,－1,0）设平面A1BC的一个法向量为n(x,y,z)，则精品学习资料可选择pdf第1页，共4页-----------------------\n学习必备欢迎下载x3nA1B0xy3z0y0nA1C0x3z0z1即n()1,0,3|nA1B1|3所以，点B1到平面A1BC的距离dz|n|2解2建系设点同上（略），设平面A1BC的方程为ax+by+cz+d=0分析思考(a,b,c,d不全为零)，把点A1，B，C三点坐标分别代入平面方程得A1C1d0a3c平面A1BC的方程为3x+z=0bd0b0B1x又B1（0,1,3）AC设点B1到平面A1BC的距离为d，则B︱3x0+1x0+3︱3d==y22(3)+12、例2（20XX年福建卷）如图，四面体ABCD中，O、E分别是BD、BC的中点，CACBCDBD2AABAD2（I）求证：AO平面BCD；（II）求异面直线AB与CD所成角的大小；D巩固练习O（III）求点E到平面ACD的距离。C解：（I）略BE（II）解：以O为原点，如图建立空间直角坐标系，则B(1,0,0),D(1,0,0),13C(0,3,0),A(0,0,1),(,E,0),BA(1,0,1),CD(1,3,0).22BACD.2cosBACD,,BACD4zA2异面直线AB与CD所成角的大小为arccos.4DO（III）解：设平面ACD的法向量为n(,,),xyz则xyBEC精品学习资料可选择pdf第2页，共4页-----------------------\n学习必备欢迎下载nAD.(,,).(1,0,1)xyz0,nAC.(,,).(0,xyz3,1)0,xz0,3yz0.令y1,得n(3,1,3)是平面ACD的一个法向量，又13EC(,,0),22ECn.321点E到平面ACD的距离h.n77四、练习练习：（2005福建卷理第20题）如图，直二面角D-AB-E中，四边形ABCD是边长为2的正方形，AE＝EB，F为CE上的点，且BF⊥平面ACE．（Ⅰ）求证：AE⊥平面BCE；（Ⅱ）求二面角B-AC-E的大小；DC（Ⅲ）求点D到平面ACE的距离。解（Ⅰ）略（Ⅱ）以线段AB的中点为原点O，OE所在直线为x轴，AB所在直线为y轴，过O点平行于AD的直线为z轴，建立空间直角坐标系O—xyz，如图.FABAE面BCE，BE面BCE，AEBE，在RtAEB中,AB,2O为AB的中点，EOE1A,0(0,1),E0,0,1(),C2,1,0().AE0,1,1(),AC2,2,0().设平面AEC的一个法向量为n(x,y,z)，AEn,0xy,0yx,则即解得ACn,02y2x.0zx,令x,1得n,1()1,1是平面AEC的一个法向量.又平面BAC的一个法向量为m)0,0,1(，m,n13cos(m,n).|m||n|333∴二面角B—AC—E的大小为arccos.3精品学习资料可选择pdf第3页，共4页-----------------------\n学习必备欢迎下载（III）∵AD//z轴，AD=2，∴AD)2,0,0(，|ADn|22∴点D到平面ACE的距离d.3|n|33五、知识小结：小结向量法求距离课后学生做题思路清晰，运用公式恰当，完成教学目标。反思精品学习资料可选择pdf第4页，共4页-----------------------