高中数学 平均变化率教案教案 新人教A版选修2-2 教案 4页

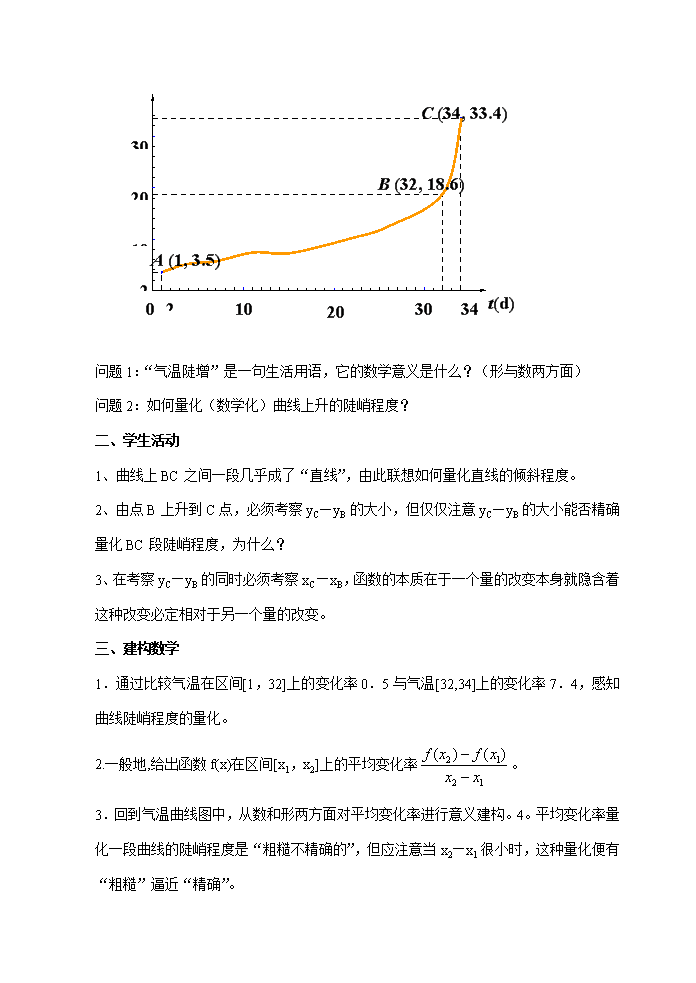
平均变化率一、教学目标1．感受平均变化率广泛存在于日常生活之中，经历运用数学描述和刻画现实世界的过程。体会数学的博大精深以及学习数学的意义。2．理解平均变化率的意义，为后续建立瞬时变化率和导数的数学模型提供丰富的背景。二、教学重点、难点重点：平均变化率的实际意义和数学意义难点：平均变化率的实际意义和数学意义三、教学过程一、问题情境1、情境：现有南京市某年3月和4月某天日最高气温记载.时间3月18日4月18日4月20日日最高气温3.5℃18.6℃33.4℃观察：3月18日到4月18日与4月18日到4月20日的温度变化，用曲线图表示为：（理解图中A、B、C点的坐标的含义）\nt(d)2030342102030A(1,3.5)B(32,18.6)0C(34,33.4)T(℃)210问题1：“气温陡增”是一句生活用语，它的数学意义是什么？（形与数两方面）问题2：如何量化（数学化）曲线上升的陡峭程度？二、学生活动1、曲线上BC之间一段几乎成了“直线”，由此联想如何量化直线的倾斜程度。2、由点B上升到C点，必须考察yC—yB的大小，但仅仅注意yC—yB的大小能否精确量化BC段陡峭程度，为什么？3、在考察yC—yB的同时必须考察xC—xB，函数的本质在于一个量的改变本身就隐含着这种改变必定相对于另一个量的改变。三、建构数学1．通过比较气温在区间[1，32]上的变化率0．5与气温[32,34]上的变化率7．4，感知曲线陡峭程度的量化。2.一般地,给出函数f(x)在区间[x1，x2]上的平均变化率。3．回到气温曲线图中，从数和形两方面对平均变化率进行意义建构。4。平均变化率量化一段曲线的陡峭程度是“粗糙不精确的”，但应注意当x2—x1很小时，这种量化便有“粗糙”逼近“精确”。\n四、数学运用例1、在经营某商品中，甲挣到10万元，乙挣到2万元，如何比较和评价甲，乙两人的经营成果？变：在经营某商品中，甲用5年时间挣到10万元，乙用5个月时间挣到2万元，如何比较和评价甲，乙两人的经营成果？小结：仅考虑一个变量的变化是不形的。例2、水经过虹吸管从容器甲中流向容器乙，ts后容器甲中水的体积（单位：），计算第一个10s内V的平均变化率。注：例3、已知函数，分别计算在下列区间上的平均变化率：（1）[1，3]；（2）[1，2]；（3）[1，1.1]；（4）[1，1.001]。\n五、课堂练习1、某婴儿从出生到第12个月的体重变化如图所示，试分别计算从出生到第3个月与第6个月到第12个月该婴儿体重的平均变化率。T(月)W(kg)639123.56.58.6112、已知函数f（x）=2x+1，g（x）=—2x，分别计算在区间[-3，-1]，[0，5]上f（x）及g（x）的平均变化率。（发现：y=kx+b在区间[m，n]上的平均变化率有什么特点？）六、回顾反思1、平均变化率一般的，函数在区间[x1，x2]上的平均变化率。２、平均变化率是曲线陡峭程度的“数量化”，曲线陡峭程度是平均变化率“视觉化”．七、作业