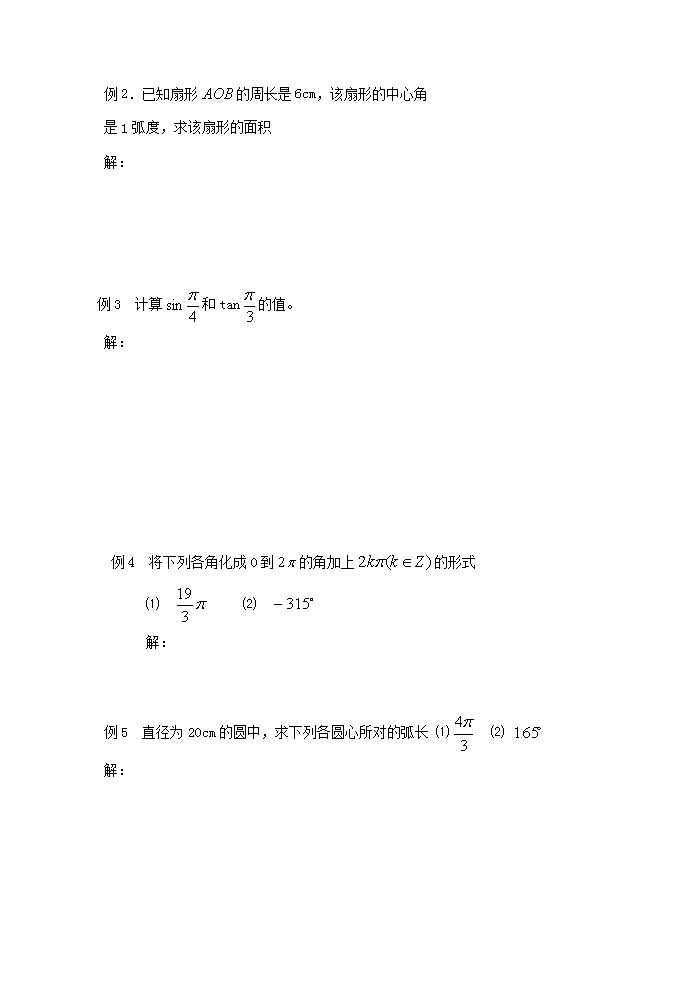高中数学(弧度制)教案5 新人教A版必修4 教案 5页

课题：弧度制（二）教学目的：巩固弧度制的理解，熟练掌握角度弧度的换算；掌握用弧度制表示的弧长公式、扇形面积公式．培养运用弧度制解决具体的问题的意识和能力教学重点：运用弧度制解决具体的问题．教学难点：运用弧度制解决具体的问题．教学过程：一、复习引入：1.360°=2prad180°=prad。2.初中学过的弧长公式、扇形面积公式：；二、讲解新课：1．弧长公式：由公式：比公式简单弧长等于弧所对的圆心角（的弧度数）的绝对值与半径的积2．扇形面积公式其中是扇形弧长，是圆的半径证：三、讲解范例：例1．求图中公路弯道处弧AB的长（精确到1m）图中长度单位为：m解：\n例2．已知扇形的周长是6cm，该扇形的中心角是1弧度，求该扇形的面积解：例3计算和tan的值。解：例4将下列各角化成0到的角加上的形式⑴⑵解：例5直径为20cm的圆中，求下列各圆心所对的弧长⑴⑵解：\n例6已知扇形周长为10cm，面积为6cm2，求扇形中心角的弧度数．解：班级姓名成绩1.圆的半径变为原来的2倍，而弧长也增加到原来的2倍，则()A.扇形的面积不变B.扇形的圆心角不变C.扇形的面积增大到原来的2倍D.扇形的圆心角增大到原来的2倍2.时钟经过一小时，时针转过了()A.radB.－radC.radD.－rad3.一个半径为R的扇形，它的周长是4R，则这个扇形所含弓形的面积是()4.圆的半径变为原来的，而弧长不变，则该弧所对的圆心角是原来的倍.5.若α＝－216°，l＝7π，则ｒ＝\n(其中扇形的圆心角为α，弧长为l，半径为r).6.在半径为的圆中，圆心角为周角的的角所对圆弧的长为.7.两个圆心角相同的扇形的面积之比为1∶2，则两个扇形周长的比为()A.1∶2B.1∶4C.1∶D.1∶88.在半径为1的单位圆中，一条弦AB的长度为，则弦AB所对圆心角α是()A.α＝B.α＜C.α＝D.α＝1209.时钟从6时50分走到10时40分，这时分针旋转了弧度.10.已知扇形AOB的面积是1cm2，它的周长是4cm，则弦AB的长等于cm.11.扇形的面积一定，问它的中心角α取何值时，扇形的周长L最小?\n12.在时钟上，自零时刻到分针与时针第一次重合，分针所转过角的弧度数是多少?