- 146.00 KB
- 2022-08-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
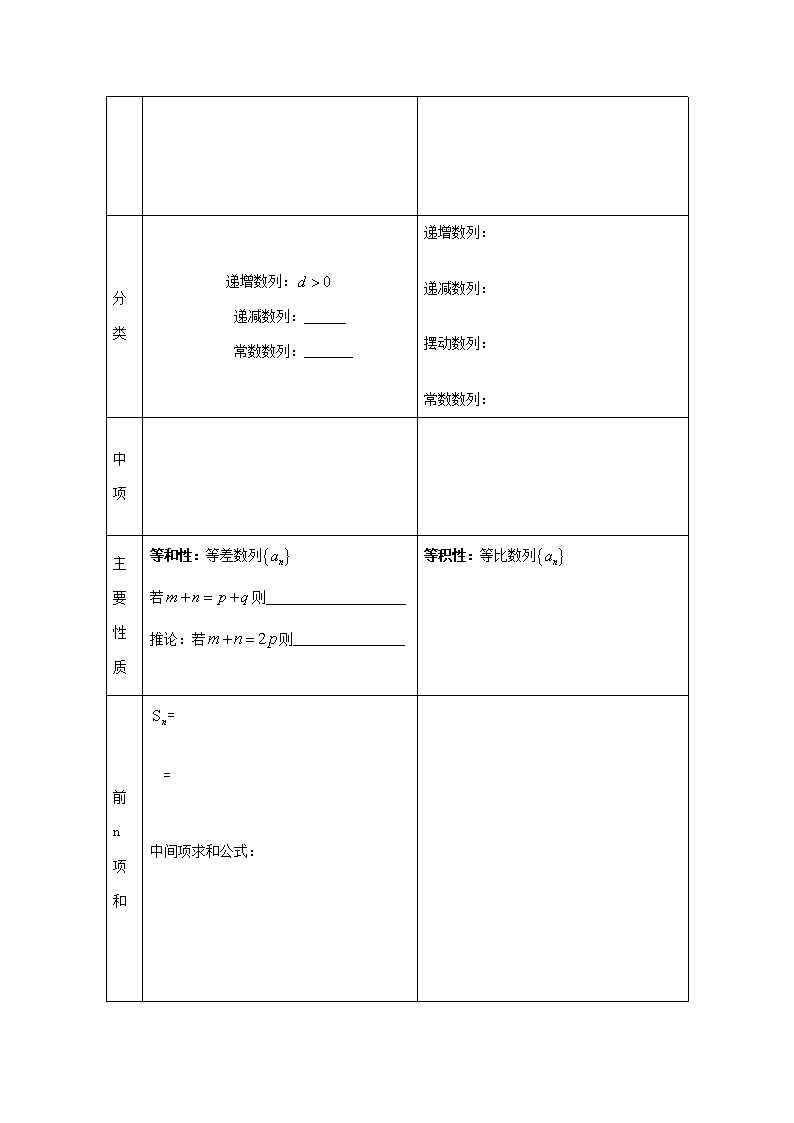
必修5数列基础知识一、等差数列与等比数列等差数列等比数列文字定义一般地,如果一个数列从第项起,每一项与它的前一项的是同一个常数,那么这个数列就叫等差数列,这个常数叫等差数列的公差。一般地,如果一个数列从第二项起,每一项与它的前一项的是同一个常数,那么这个数列就叫等比数列,这个常数叫等比数列的符号定义通项公式对应函数图像等差数列的通项公式是的一次函数。等比数列的通项公式类似于的指数函数,即:,其中\n分类递增数列:递减数列:常数数列:递增数列:递减数列:摆动数列:常数数列:中项主要性质等和性:等差数列若则推论:若则等积性:等比数列前n项和==中间项求和公式:\n对应函数图像是关于的一个的二次函数,即:()等比数列的前项和公式是一个平移加振幅的的指数函数,即:其它性质1、等差数列中连续项的和,组成的新数列是等差数列。即:等差,公差为2、从等差数列中抽取等距离的项组成的数列是一个等差数列。如:(下标成等差的子数列为数列)3、等差,则,,,是数列。1、等比数列中连续项的和,组成的新数列是数列。即:等比,公比为。2、从等比数列中抽取等距离的项组成的数列是一个等比数列。如:(下标成等差的子数列为数列)3、等比,则,,,是数列。其中\n4、在等差数列中,为等差数列4、等比数列中连续相同项数的积组成的新数列是等比数列。如:,,证明方法证明一个数列为等差数列的方法:1、定义法:2、中项法:证明一个数列为等比数列的方法:1、定义法:2、中项法:设元技巧三数等差:四数等差:三数等比:四数等比:联系1、若数列是等差数列,则数列是等比数列,公比为,其中是常数,是的公差。2、若数列是等比数列,且,则数列是等差数列,公差为,其中是常数且,是的公比。二、已知求的关递推公式:三、等差数列前项和的最值问题:1、若等差数列的首项,公差,则前项和有最大值。(ⅰ)若已知通项,则最大;(ⅱ)若已知,则当取最靠近对称轴的非零自然数时最大;2、若等差数列的首项,公差,则前项和有最小值\n(ⅰ)若已知通项,则最小;(ⅱ)若已知,则当取最靠近对称轴的非零自然数时最小;四、数列求和的常用方法:1、拆项分组法:即把每一项拆成几项,重新组合分成几组,转化为特殊数列求和。2、错项相减法:适用于差比数列(如果等差,等比,那么叫做差比数列)即把每一项都乘以的公比,向后错一项,再对应同次项相减,转化为等比数列求和。3、裂项相消法:即把每一项都拆成正负两项,使其正负抵消,只余有限几项,可求和。 适用于数列和(其中等差) 可裂项为:,五、根据递推公式求通项:已知,(是常数),求;例如:①、已知,,求;②、已知,,求;(提示:令,则,则数列是以为首项,3为公比的等比数列,所以,即)六、本章重要思想方法:方程思想;