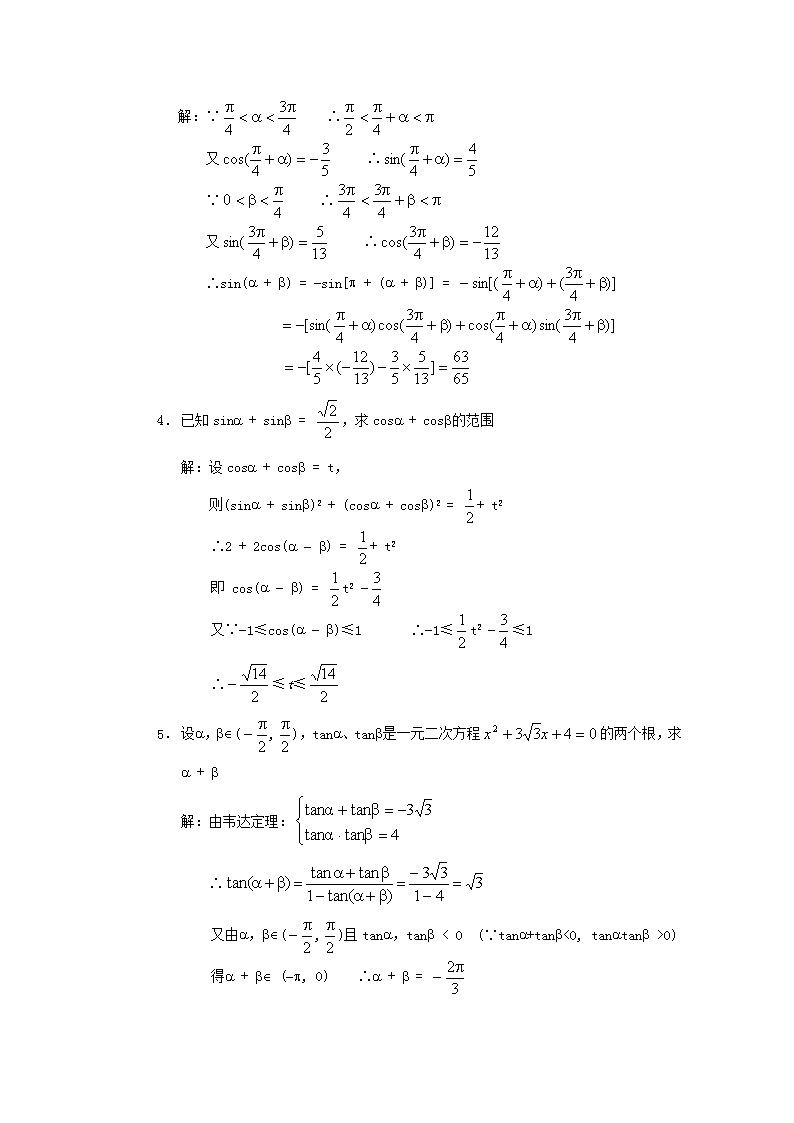高中数学 三角函数系列课时教案38 教案 3页

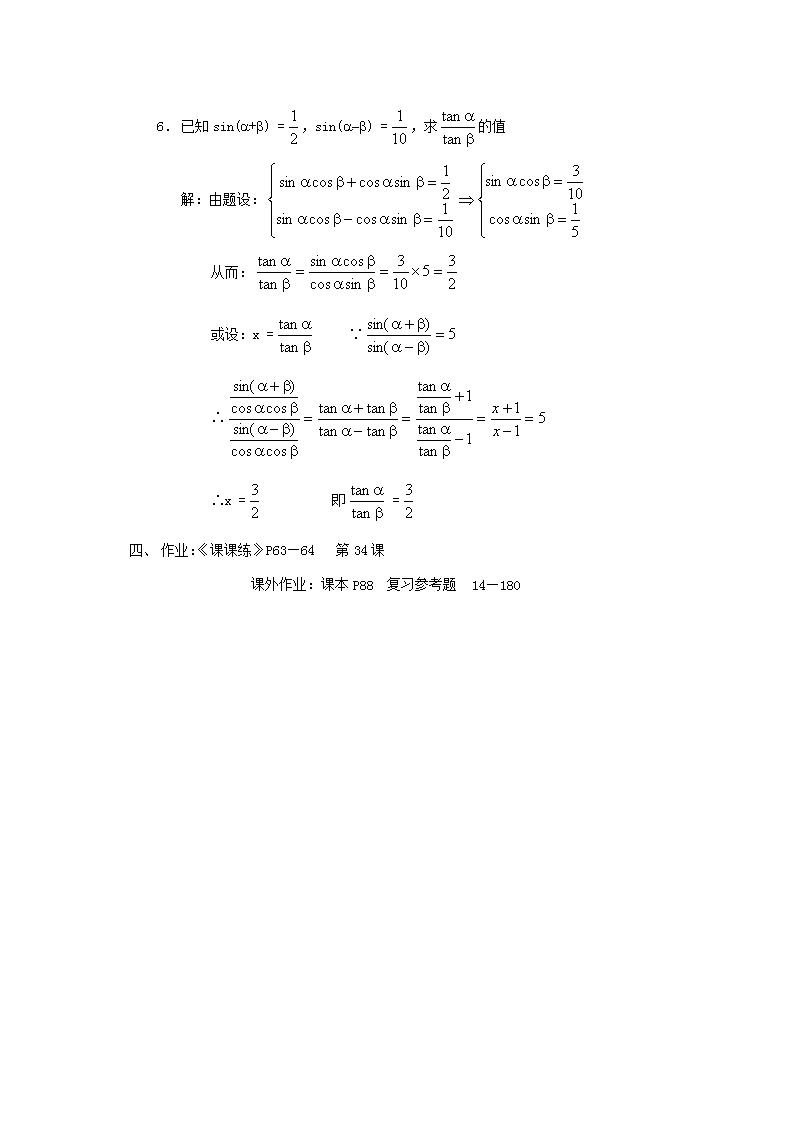
第三十八教时三角函数教材：复习两角和与差的三角函数（用《导学创新》）目的：通过复习让学生进一步熟悉有关内容，并正确运用有关技巧解决具体问题。过程：一、复习：有关公式二、强调有关解题技巧：化弦、辅助角、角变换、公式逆用、正余弦和积互换三、例题：1．在△ABC中，已知cosA=，sinB=，则cosC的值为…………（A）A.B.C.D.解：∵C=p-(A+B)∴cosC=-cos(A+B)又∵AÎ(0,p)∴sinA=而sinB=显然sinA>sinB∴A>B即B必为锐角∴cosB=∴cosC=-cos(A+B)=sinAsinB-cosAcosB=2．在△ABC中，ÐC>90°，则tanAtanB与1的关系适合………………（B）A.tanAtanB>1B.tanAtanB>1C.tanAtanB=1D.不确定解：在△ABC中∵ÐC>90°∴A,B为锐角即tanA>0,tanB>0又：tanC<0于是：tanC=-tan(A+B)=<0∴1-tanAtanB>0即：tanAtanB<1又解：在△ABC中∵ÐC>90°∴C必在以AB为直径的⊙O内（如图）ACDhh'C’过C作CD^AB于D，DC交⊙O于C’，设CD=h，C’D=h’，AD=p，BD=q，pqB则tanAtanB3．已知，，，，求sin(a+b)的值\n解：∵∴又∴∵∴又∴∴sin(a+b)=-sin[p+(a+b)]=1．已知sina+sinb=，求cosa+cosb的范围解：设cosa+cosb=t，则(sina+sinb)2+(cosa+cosb)2=+t2∴2+2cos(a-b)=+t2即cos(a-b)=t2-又∵-1≤cos(a-b)≤1∴-1≤t2-≤1∴≤t≤2．设a，bÎ(,)，tana、tanb是一元二次方程的两个根，求a+b解：由韦达定理：∴又由a，bÎ(,)且tana，tanb<0(∵tana+tanb<0,tanatanb>0)得a+bÎ(-p,0)∴a+b=\n1．已知sin(a+b)=，sin(a-b)=，求的值解：由题设：从而：或设：x=∵∴∴x=即=三、作业：《课课练》P63—64第34课课外作业：课本P88复习参考题14—180