高中数学 三角函数系列课时教案11 教案 2页

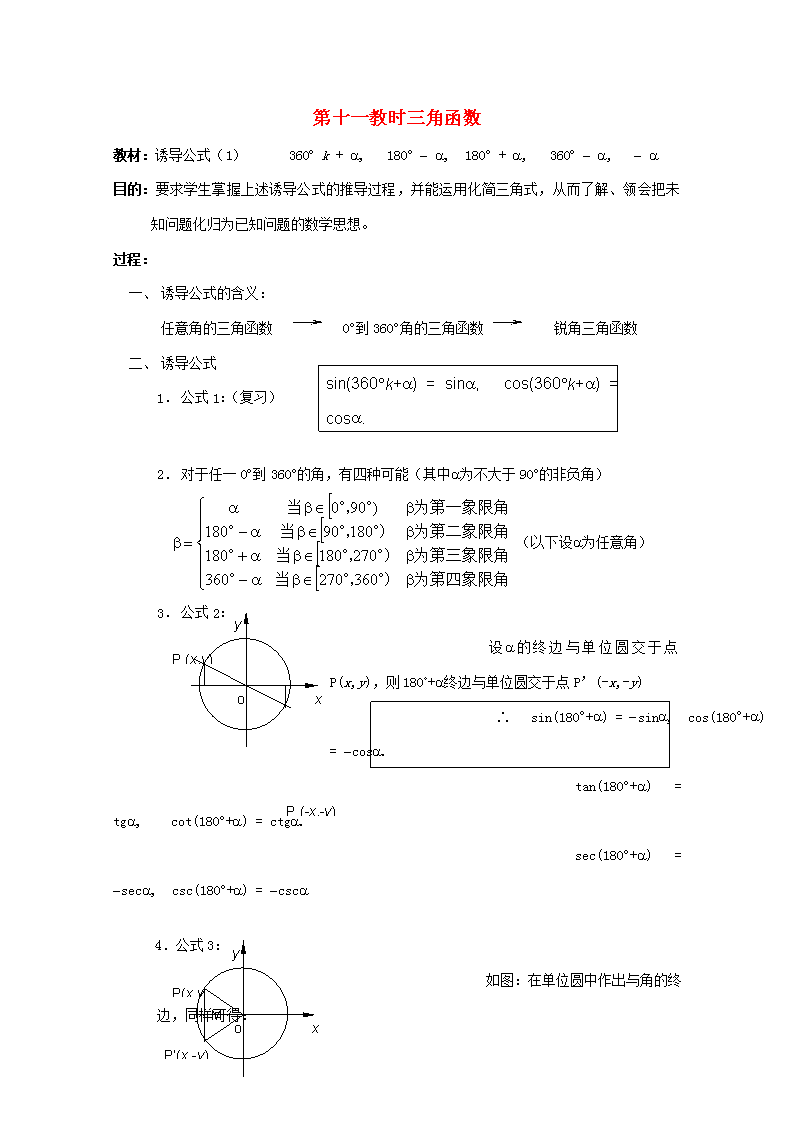
第十一教时三角函数教材：诱导公式（1）360°k+a,180°-a,180°+a,360°-a,-a目的：要求学生掌握上述诱导公式的推导过程，并能运用化简三角式，从而了解、领会把未知问题化归为已知问题的数学思想。过程：一、诱导公式的含义：任意角的三角函数0°到360°角的三角函数锐角三角函数sin(360°k+a)=sina,cos(360°k+a)=cosa.tan(360°k+a)=tga,cot(360°k+a)=ctga.sec(360°k+a)=seca,csc(360°k+a)=csca二、诱导公式1．公式1：（复习）2．对于任一0°到360°的角，有四种可能（其中a为不大于90°的非负角）（以下设a为任意角）xyoP(x,y)3．公式2：设a的终边与单位圆交于点P(x,y)，则180°+a终边与单位圆交于点P’(-x,-y)∴sin(180°+a)=-sina,cos(180°+a)=-cosa.P(-x,-y)tan(180°+a)=tga,cot(180°+a)=ctga.sec(180°+a)=-seca,csc(180°+a)=-cscaxyoP’(x,-y)P(x,y)M4．公式3：如图：在单位圆中作出与角的终边，同样可得：\nsin(-a)=-sina,cos(-a)=cosa.tan(-a)=-tana,cot(-a)=-cota.sec(-a)=seca,csc(-a)=-csca5．公式4：sin(180°-a)=sin[180°+(-a)]=-sin(-a)=sina,cos(180°-a)=cos[180°+(-a)]=-cos(-a)=-cosa,同理可得：sin(180°-a)=sina,cos(180°-a)=-cosa.tan(180°-a)=-tana,cot(180°-a)=-cota.sec(180°-a)=-seca,csc(180°-a)=csca6．公式5：sin(360°-a)=-sina,cos(360°-a)=cosa.tan(360°-a)=-tana,cot(360°-a)=-cota.sec(360°-a)=seca,csc(360°-a)=-csca三、小结：360°k+a,180°-a,180°+a,360°-a,-a的三角函数值等于a的同名三角函数值再加上一个把a看成锐角时原函数值的符号四、例题：P29—30例一、例二、例三P31—32例四、例五、例六略五、作业：P30练习P32练习P33习题4.5