高中物理有界磁场问题归类复习教案 8页

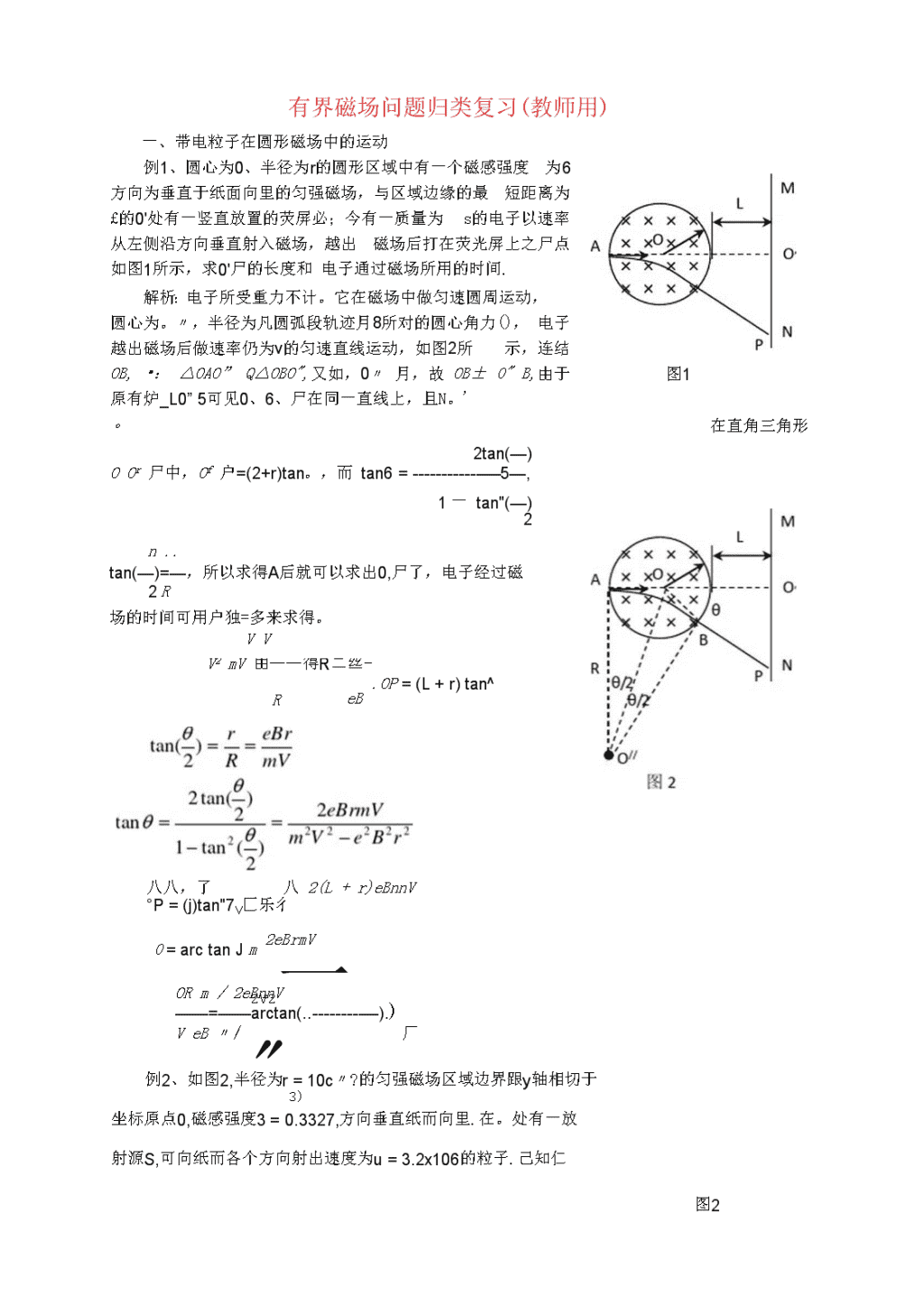
有界磁场问题归类复习(教师用)一、带电粒子在圆形磁场中的运动例1、圆心为0、半径为r的圆形区域中有一个磁感强度为6、方向为垂直于纸面向里的匀强磁场，与区域边缘的最短距离为£的0'处有一竖直放置的荧屏必；今有一质量为s的电子以速率〃从左侧沿方向垂直射入磁场，越出磁场后打在荧光屏上之尸点，如图1所示，求0'尸的长度和电子通过磁场所用的时间.解析：电子所受重力不计。它在磁场中做匀速圆周运动，圆心为。〃，半径为凡圆弧段轨迹月8所对的圆心角力()，电子越出磁场后做速率仍为v的匀速直线运动，如图2所示，连结OB,•：△OAO”Q△OBO",又如，0〃月，故OB±0"B,由于原有炉_L0”5可见0、6、尸在同一直线上，且N。'°2tan(—)OOr尸中，Of户=(2+r)tan。，而tan6=5—,1一tan"(—)2图1在直角三角形n..tan(—)=—，所以求得A后就可以求出0,尸了，电子经过磁2R场的时间可用户独=多来求得。VVV2mV由——得R二丝-.OP=(L+r)tan^ReB八八，了八2(L+r)eBnnV°P=(j)tan"7V匚乐彳0=arctanJm2V2一"3)2eBrmVORm/2eBnnV——=——arctan(..).)VeB〃/厂例2、如图2,半径为r=10c〃?的匀强磁场区域边界跟y轴相切于坐标原点0,磁感强度3=0.3327,方向垂直纸而向里.在。处有一放射源S,可向纸而各个方向射出速度为u=3.2x106的粒子.己知仁图2\n粒子质量机=6.64x10-”Ag,电量q=3.2xl0T9。，试画出。粒子通过磁场空间做圆周运动的圆心轨道，求出a粒子通过磁场空间的最大偏角.2解析：设粒子在洛仑兹力作用下的轨道半径为R,由氏=得RR=—=Bqm=0.20/7;=20cm6.64xI0-27x3.2x1060.332x3.2xlO-19虽然a粒子进入磁场的速度方向不确定，但粒子进场点是确定的，因此夕粒子作圆周运图2动的圆心必落在以0为圆心，半径R=20。〃的圆周上，如图2中虚线.由几何关系可知，速度偏转角总等于其轨道圆心角.在半径R一定的条件下，为使。粒子速度偏转角最大，即轨道圆心角最大，应使其所对弦最长.该弦是偏转轨道圆的弦，同时也是圆形磁场的弦.显然最长弦应为匀强磁场区域圆的直径.即&粒子应从磁场圆直径的A端射出.如图2,作出磁偏转角0及对应轨道圆心O',据几何关系得sing='=,，得。=60°,即a粒子穿过磁场空间的最大偏转角为60°.2R2二、带电粒子在半无界磁场中的运动例3、(1999年高考试题)如图3中虚线MN是一垂直纸面的平面与纸而的交线,在平面右侧的半空间存在一磁感应强度为氏方向垂直纸而向外的匀强磁场.。是上的一点，从。点可以向磁场区域发射电荷量为+外质量为卬、速率为血粒子，粒子射入磁场时的速度可在纸面内各个方向，己知先后射入的两个粒子恰好在磁场中给定的尸点相遇，尸到。点的距离为L,不计重力和粒子间的相互作用.(1)求所考察的粒子在磁场中的轨道半径.(2)求这两个粒子从。点射入磁场的时间间隔.解析：(1)粒子的初速度与匀强磁场的方向垂直,在洛仑兹力作用下,做匀速圆周运动.设圆半径为/?,则据牛顿第二定律可得：2Bqv=m—,解得R=—RBq⑵如图3所示，以0?为弦的可以画出两个半径相同的圆，分别表示在P点相遇的两个粒子的轨道，圆心分别为a和a,在。处两个圆的切线分别表示两个粒子的射入方向，它们之间的夹角为a,由几何关系知乙POQm乙P0z2a从。点射入到相遇，粒子在1的路径为半个圆周加2P弧长等于粒子在2的路径为半个圆周减仪尸弧长等于aR.1Ra粒子1的运动时间t^-T+—2v\ny/cmxxxxxxxx"~7\/cmXXXxXXXX图4iRa粒子2的运动时间—2vRa两个粒子射入的时间间隔△9=t-t,=2—v1|-1l由几何关系得kcos—。二一二一乙解得：a=2arccos——2222R山aLBq故Xt=-arccosBq2mv例4、如图4所示，在真空中坐标.my平面的x>0区域内，有磁感强度8=1.0xl0-2r的匀强磁场，方向与wy平面垂直，在x轴上的〃（1。,0）点，有一放射源，在my平而内向各个方向发射速率u=l.OxlO'm/s的带正电的粒子，粒子的质量为〃?=1.6x10-”匕，电量为9=1.6x1OF。，求带电粒子能打到轴上的范围.2解析：带电粒子在磁场中运动时有8少=〃?二，则Rnmv1.6xl0-25xl.OxlO4八，R=——=—=0.1///=lOcni.Bq1.0x10-2xL6xl0-"如图15所示,当带电粒子打到y轴上方的A点与P连线正好为其圆轨迹的直径时，A点既为粒子能打到y轴上方的最高点.因Op=R=\0cm,AP=2R=20cm,则OA=VAP—OP=10y/3cm.当带电粒子的圆轨迹正好与y轴下方相切于B点时，R点既为粒子能打到y轴下方的最低点，易得丽=R=10sn.综上，带电粒子能打到y轴上的范围为：一10c〃?vXXXdXXXX正电粒子（重力不计），从左侧两极板的中心处以不同速率P水平射入，欲使粒子不打在板上，求粒子速率U应满足什么条件.图5\n综上，要粒子不打在板上，其入射速率应满足:”驷或”坐出也.4〃？4md解析：如图4,设粒子以速率匕运动时，粒子正好打在左极板边缘（图4中轨迹1）,则其圆轨迹半径为凡=",又由8Gl=加上得当=0%，则粒4与4/77子入射速率小于匕时可不打在板上.设粒子以速率也运动时，粒子正好打在右极板边缘（图4中轨迹2）,由图可得兄2=乙2+（凡一“）2,则其圆轨迹半径为--2R,=,又由Bqv、=m二得匕=%（41十^）,则粒44-网-4〃W例6、长为£的水平极板间，有垂直纸面向内的匀强磁场，如图4所示，磁感强度为£板间距离也为乙板不带电，现有质量为山，电量为q的带正电粒子（不计重力），从左边极板间中点处垂直磁感线以速度/水平射入磁场，欲使粒子不打在极板上，可采用的办法是：A.使粒子的速度VBqL/mxD.使粒子速度的2/4冰火5%£/4s解析：由左手定则判得粒子在磁场中间向上偏，而作匀速圆周运动，很明显，圆周运动的半径大于某值八时粒子可以从极板右边穿出，而半径小于某值三时粒子可从极板的左边穿出，现在问题归结为求粒子能在右边穿出时r的最小值r：以及粒子在左图6边穿出时r的最大值毛，由几何知识得：粒子擦着板从右边穿出时，圆心在。点，有：=；=二+（八-£/2尸得八二5£/4,又由于八二卬匕/’的得匕=5的£/4典，J05万qZ.AU时粒子能从右边穿出。粒子擦着上板从左边穿出时，圆心在0'点，有八=£/4,又由r.=mVz/BcpL/\得Vz=BqL/\m・••V《BqU4m时粒子能从左边穿出o综上可得正确答案是A、B。四、带电粒子在“三角形磁场区域”中的运动例7、在边长为2a的AA8C内存在垂直纸面向里的磁感强度为8的匀强磁场，有一带正电ty,质量为6的粒子从距A点、氐”的D点垂子入射速率大于叱时可不打在板上.\n直AB方向进入磁场，如图5所示，若粒子能从AC间离开磁场，求粒子速率应满足什么条件及粒子从AC间什么范围内射出.解析：如图6所示，设粒子速率为匕时，其圆轨迹正好与AC边相切于E点.由图知，在中，印=R,@=,由cos30°=生得亘=-^一，解得g=3（2—JJ）〃，则aA2品I-R\通=空=在旦=（2百—3"22又由Bq%=，〃工得%=也&=3（”史）〃”,则要粒子能尺tnm从AC间离开磁场，其速率应大于%.如图7所示，设粒子速率为叱时，其圆轨迹正好与BC边相切于F点，与AC相交于G点.易知A点即为粒子轨迹的圆心，则/?2=而=芯=限.又由Bqv2=得％=史丝四，则要粒子能从AC间离开磁场，其速率应小于等・m于'综上，要粒子能从AC间离开磁场，粒子速率应满足3Q-6)aqBmm粒子从距A点（2、后一3）。~瓜的EG间射出.五、带电粒子在“宽度一定的无限长磁场区域”中的运动例8、如图11所示，A、B为水平放置的足够长的平行板，板间距离为4=1.0x10-2〃?，A板中央有一电子源P,在纸面内能向各个方向发射速度在0~3.2x107〃?/$范围内的电子，q为p点正上方b板上的一点，若垂直BQr~\XX：XX+纸而加一匀强磁场，磁感应强度8=9.1x10-37,已知电子的质量x'修x〃7=9,lxlO-3〃g,电子电量e=L6xl（）T'C,不计电子的重力和电子图8=间相互作用力，且电子打到板上均被吸收，并转移到大地.求：（1）沿PQ方向射出的电子击中A、B两板上的范围.（2）若从P点发出的粒子能恰好击中Q点，则电子的发射方向（用图中6角表示）与\n电子速度的大小I，之间应满足的关系及各自相应的取值范围.解析：如图12所示，沿PQ方向射出的电子最大轨迹半径由Bev=m9可得%=生，代入数据解得乙“=2x10々m=2d.x\APFH该电子运动轨迹圆心在A板上H处，恰能击中B板M处.随着,电子速度的减少，电子轨迹半径也逐渐减小.击中B板的电子与Q图12点最远处相切于N点，此时电子的轨迹半径为4,并恰能落在A板上H处.所以电子能击中B板MN区域和A板PH区域.图13在AMFH中，有TH=用而、而F=&2d)2,QM=而=(2-5d=2.68xi0-3m/s,函="=1x10-2m，丽=2J=2xK)-2〃？电子能击中B板Q点右侧与Q点相距2.68x10-3-]xICT:/〃的范用.电子能击中A板P点右恻与P点相距。〜2xIO*加的范围.（2）如图13所示，要使P点发出的电子能击中Q点，则有r=竺.rsin8=".Be2y/cmxxxxxxxxXjxx,/cmXXXX图14解得usin6=8xlOTv取最大速度3.2xWm/s时，有sin<9=1,4纥而=arcsin1：u取最小速度时有iX=—，111IIIIIIUA2Pmin=8xl06/H/5.所以电子速度与6之间应满足vsm^=8xl06,且0e[arcsin—,—],ve[8x106/n/5,3.2x10mis}六、带电粒子在相反方向的两个有界磁场中的运动例9、如图9所示，空间分布着有理想边界的匀强电场和匀强磁场.左侧匀强电场的场强大小为反方向水平向右，电场宽度为£：中间区域匀强磁场的磁感应强度大小为6,方向垂直纸面向里.一个质量为外电量为外不计重力的带正电的粒子从电场的左边缘的0点由静止开始运动，穿过中间磁场区域进入右侧磁场区域后，又回到。点，然后重复上述运动过程.求:（1）中间磁场区域的宽度d;（2）带电粒子从。点开始运动到第一次回到0点所用时图9\n解析：（1）带电粒子在电场中加速，由动能定理，可得：qEL=-mV22带电粒子在磁场中偏转，由牛顿第二定律，可得：V2BqV=m——R由以上两式，可得RB在中间磁场中运动时间b=-=—33qB可见在两磁场区粒子运动半径相同，如图11所示，三段圆弧的圆心组成的三角形△aaa是等边三角形，其边长为2兄所以中间磁场区域的宽度为,d-Ano16nELd=/?sm60=——i2B\q(2)在电场中2V2mV12mLf\=-=7T=2।——，aqE\qE在右侧磁场中运动时间右==四,63qB则粒子第一次回到。点的所用时间为图10七、带电粒子在环形或有孔磁场中的运动例10、核聚变反应需要几百万度以上的高温，为把高温条件下高速运动的离子约束在小范闱内（否则不可能发生核反应），通常采用磁约束的方法（托卡马克装置）。如图5所示，环状匀强磁场围成中空区域，中空区域中的带电粒子只要速度不是很大，都不会穿出磁场的外边缘而被约束在该区域内。设环状磁场的内半径为兄=0.5m,外半径凡=1.0m,磁场的磁感强度后L0T,若被束缚带电粒子的荷质比为q后4X107C/kg,中空区域内带电粒子具有各个方向的速度.试计算（1）粒子沿环状的半径方向射入磁场，不能穿越磁场的最大速度.（2）所有粒子不能穿越磁场的最大速度.解析：（1）要粒子沿环状的半径方向射入磁场，不能穿越磁场，则粒子的临界轨迹必须要与外圆相切，轨迹如图6所示.由图中知八2+R；=（/?2-八『，解得八=。.375〃?\n由8夕匕=〃7工得匕=Bq,\=1.5x10%/$7|m所以粒子沿环状的半径方向射入磁场，不能穿越磁场的最大速度为匕=1.5x10〃?/$.(2)当粒子以上的速度沿与内圆相切方向射入磁场且轨道与外圆相切时，则以匕速度沿各方向射入磁场区的粒子都不能穿出磁场边界,如图7所示.R_R由图中知q=~-=0.25/??由BqV?=〃?、-得匕==l.Ox10nils'm所以所有粒子不能穿越磁场的最大速度V.=1.0xl07mls一图7其上均匀分布着平行于例11、如图8所示，两个共轴的圆筒形金属电极，外电极接地,轴线的四条狭缝a、b、c和d,外筒的外半径为r,在圆筒之外的足够大区域中有平行于轴线方向的均匀磁场，磁感强度的大小为6.在两极间加上电压，使X两圆筒之间的区域内有沿半径向外的电场.一质量为"人带电量为+g的粒子，从紧靠内筒且正对狭缝a的S点出发，初速为零。*如果该粒子经过一段时间的运动之后恰好又回到出发点S,则两x电极之间的电压〃应是多少？(不计重力，整个装置在真空中)解析：如图9所示，带电粒子从S点出发，在两筒之间的X电场作用下加速，沿径向穿过狭缝a而进入磁场区，在洛伦兹力作用下做匀速圆周运动.粒子再回到S点的条件是能沿径向穿过狭缝d.只要穿过了d粒子就会在电场力作用下先减速，再反向图11XXXX加速，经d重新进入磁场区，然后粒子以同样方式经过°、b,再回到S点。设粒子进入磁场区的速度大小为V,根据动能定理，有qU=^mV2设粒子做匀速圆周运动的半径为尼由洛伦兹力公式和牛顿第二定律，有V2BqV=m——R由前面分析可知，要回到S点，粒子从&到d必经过上圆周，所4图9以半径斤必定等于简的外半径r，即庐工由以上各式解得；U二号2m