- 186.39 KB
- 2022-08-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
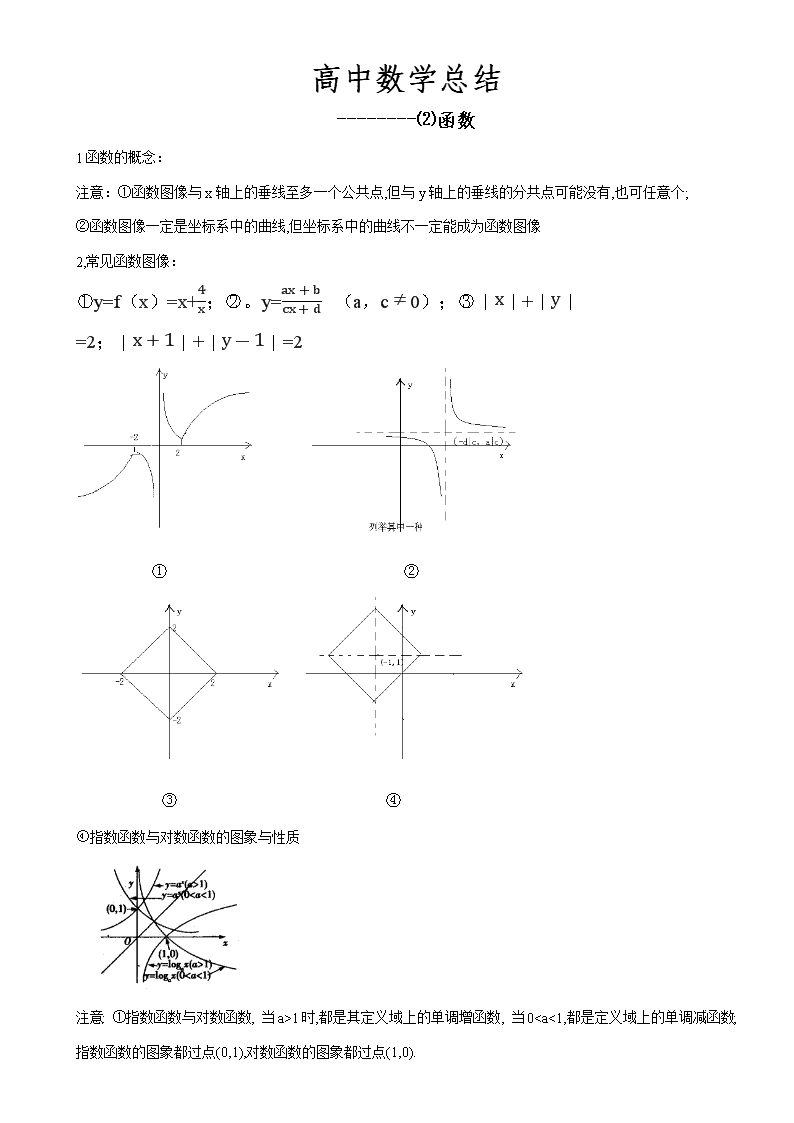
高中数学总结--------⑵函数1函数的概念:注意:①函数图像与x轴上的垂线至多一个公共点,但与y轴上的垂线的分共点可能没有,也可任意个;②函数图像一定是坐标系中的曲线,但坐标系中的曲线不一定能成为函数图像2,常见函数图像:y=f(x)=x+4x;。y=ax+bcx+d(a,c≠0);|x|+|y|=2;|x+1|+|y-1|=2指数函数与对数函数的图象与性质注意:①指数函数与对数函数,当a>1时,都是其定义域上的单调增函数,当00,且,若f(x)的值域为R,则a>0,且..幂函数:注意:幂指数大于0时,幂函数在(0,+∝)上单调递增;幂指数小于0时,幂函数在(0,+∞)上单调递减,所有幂函数的图象都过点(1,1).3图形变换:高中阶段主要学习了种函数:常数函数,n次函数,幂函数(xa),指数函数,对数函数,三角函数,分段函数(如含绝对值的函数)①加减变换:遵循“左加右减,上加下减”的原则(其中上加下减是在X一方变换的,如果也针对y则为“下加上减”即y=f(x)按向量(a,b)平移为y-b=f(x-a)。)②伸缩变换:y=f(x)→y=f(ax)即沿x轴方向向y轴变为原来的1a。绝对值的变换:y=f(x),y=f(|x|),y=|f(x)|,|y|=f(x)的相互转换。4,函数的常见性质若函数y=f(x)满足f(a+bx)=f(c-bx),,则f(mx)的图像关于x=a+bx+c-bx2m=a+c2m对称对一函数y=f(x),有y=f(a+bx)与y=f(c-bx)的图像关于a+bx=c-bx,即x=c-a2b,对称若y=f(x+a)的图像关于y轴对称,则有f(x+a)=f(-x+a),及f(x)关于x=a对称函数f(x)=ax+bcx+d(a,c≠0)值域为x|x≠ac,图像关于点(-dc,ac)中心对称。(其实该函数是由反比例函数经过平移或伸缩变换而得,而反比例函数就刚好关于原点中心对称。)若f(x)=ax+bcx+d(a,c≠0)则f-1(x)==dx-b-cx+a,(a,d对调)周期函数不一定有最小正周期。如狄利克雷函数D(X)=fx=1,&x为有理数0,&x为无理数这是一个周期函数,任何正有理数都是它的周期,但是它不存在最小正周期。\n原函数与反函数的奇偶性和单调性相同,原函数与导函数的奇偶性相反。设a为非0常数,若f(x)在定义域内恒有下列条件之一:I,f(x+a)=--f(x),II,f(x+a)f(x)=1,III,f(x+a)=f(x)+1f(x)-1IV,f(x+a)=f(x—a)。则f(x)为周期函数,2a为其周期。若f(x)同时关于x=a和x=b对称,则2b-2a为一周期若f(x)关于x=a对称,且关于点(b,0)对称(a与b不相等)则4b-4a为其一周期若f(x)同时关于点(a,0)和点(b,0)对称,则2b-2a为其一周期。5函数与不等式的求解(详见函数与不等式,导数章节)6抽象函数问题抽象函数性质特殊函数模型f(x1+x2)=f(x1)+f(x2)f(x)=kxf(x1+x2)=f(x1).f(x2)或f(x1-x2)=f(x1)∕f(x2)f(x)=axf(x1x2)=f(x1)+f(x2)或f(x1∕x2)=f(x1)-f(x2)f(x)=logaxf(x1)+f(x2)=2f(x1+x2)∕2f(x1-x2)∕2f(x)=cosx易错点;1,忽略了函数的定义域,造成范围求解是出错。2,告知截距相等时,要考虑y=kx的情况,此时截距均为03,求一个函数的解析式和一个函数的反函数时,记得标注该函数的定义域了。例1、在同一坐标系中,函数与(>0且≠1)的图象可能是\n(A)(B)(C)(D)例2、设,,,则的面积是()A.1B.C.4D.4例3、若定义在区间上的函数对上的任意个值,,…,,总满足≤,则称为上的凸函数.已知函数在区间上是“凸函数”,则在△中,的最大值是____________________.答案;1,C.2,B3,。例4.已知,求的最大值与最小值。,,。例5,设方程的两个根为,则()ABCD由两图象交点的意义,交点的横坐标分别为不妨设\n,利用方程根适合方程,注意绝对值的意义化为如何确定范围?目标函数变形,,选D.例6,对于三次函数。定义:(1)设是函数的导数的导数,若方程有实数解,则称点为函数的“拐点”;定义:(2)设为常数,若定义在上的函数对于定义域内的一切实数,都有成立,则函数的图象关于点对称。己知,请回答下列问题:(1)求函数的“拐点”的坐标(2)检验函数的图象是否关于“拐点”对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)(3)写出一个三次函数,使得它的“拐点”是(不要过程)【标准答案】(1)依题意,得:,。……………………2分由,即。∴,又,∴的“拐点”坐标是。……………………4分(2)由(1)知“拐点”坐标是。而===,由定义(2)知:关于点对称。……………………8分一般地,三次函数的“拐点”是,它就是的对称中心。………………………………………………………………………10分(或者:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;任何一个三次函数平移后可以是奇函数………)都可以给分\n(3)或写出一个具体的函数,如或。…………12分说明:本题在函数、导数、方程的交汇处命题,具有较强的预测性,而且设问的方式具有较大的开放性,情景新颖.解题的关键是:深刻理解函数“拐点”的定义和函数图像的对称中心的意义。其本质是:任何一个三次函数都有拐点;任何一个三次函数都有对称中心;