高中数学新课极限教案(3) 5页

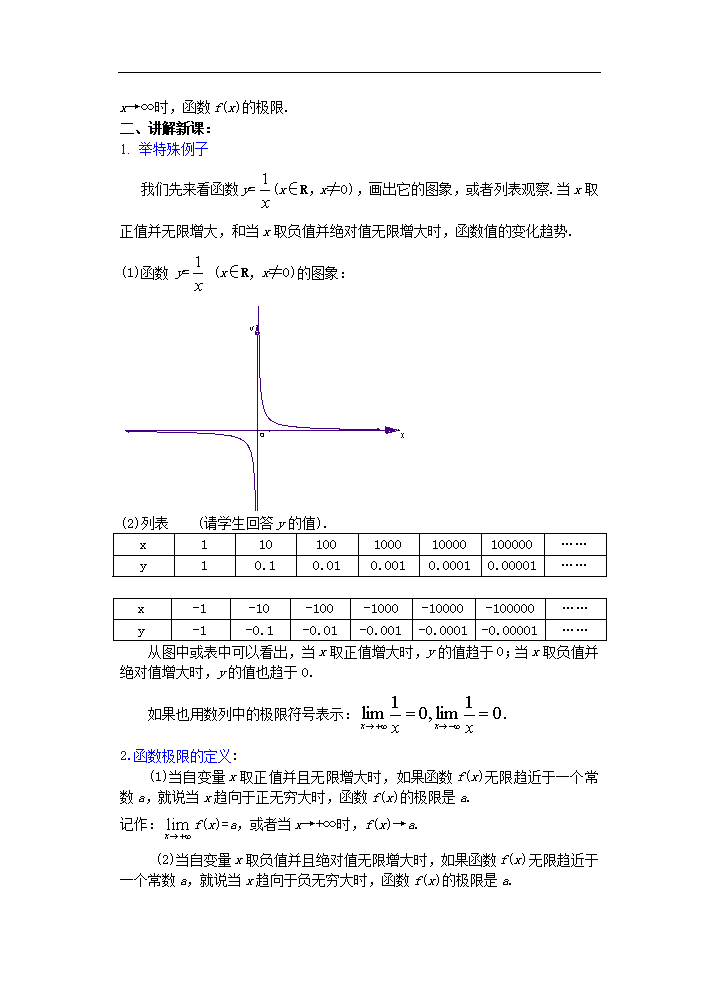
课题：2.3函数的极限(一)教学目的：1.理解当x→+∞，x→－∞，x→∞时，函数f(x)的极限的概念.2.从函数的变化趋势，理解掌握函数极限的概念.3.会求当函数的自变量分别趋于+∞，－∞，∞时的极限教学重点：从函数的变化趋势来理解极限的概念，体会极限思想.教学难点：对极限概念如何可从变化趋势的角度来正确理解.授课类型：新授课课时安排：1课时教具：多媒体、实物投影仪教学过程：一、复习引入：1.数列极限的定义：一般地，如果当项数无限增大时，无穷数列的项无限趋近于某个常数（即无限趋近于0），那么就说数列以为极限，或者说是数列的极限．记作，读作“当趋向于无穷大时，的极限等于”“∞”表示“趋向于无穷大”，即无限增大的意思有时也记作：当∞时，．理解：数列的极限的直观描述方式的定义，只是对数列变化趋势的定性说明，而不是定量化的定义.“随着项数n的无限增大，数列的项an无限地趋近于某个常数a”的意义有两个方面：一方面，数列的项an趋近于a是在无限过程中进行的，即随着n的增大an越来越接近于a；另一方面，an不是一般地趋近于a，而是“无限”地趋近于a，即|an－a|随n的增大而无限地趋近于0.2.几个重要极限：（1）（2）（C是常数）（3）无穷等比数列（）的极限是0，即3.将an看成是n的函数即an=f(n).自变量n∈N*，an就是一个特殊的函数.数列的项an,随着n的增大an越来越接近于a,也就是f(n)越来越接近于a．对于一般的函数f(x)，自变量x∈R，是否有同样的结论呢？这节课就来研究当\nx→∞时，函数f(x)的极限.二、讲解新课：1.举特殊例子我们先来看函数y=(x∈R，x≠0)，画出它的图象，或者列表观察.当x取正值并无限增大，和当x取负值并绝对值无限增大时，函数值的变化趋势.(1)函数y=(x∈R，x≠0)的图象：(2)列表(请学生回答y的值).x110100100010000100000……y10.10.010.0010.00010.00001……x-1-10-100-1000-10000-100000……y-1-0.1-0.01-0.001-0.0001-0.00001……从图中或表中可以看出，当x取正值增大时，y的值趋于0；当x取负值并绝对值增大时，y的值也趋于0.如果也用数列中的极限符号表示：.2.函数极限的定义:(1)当自变量x取正值并且无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于正无穷大时，函数f(x)的极限是a.记作：f(x)=a，或者当x→+∞时，f(x)→a.(2)当自变量x取负值并且绝对值无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于负无穷大时，函数f(x)的极限是a.\n记作f(x)=a或者当x→－∞时，f(x)→a.(3)如果f(x)=a且f(x)=a，那么就说当x趋向于无穷大时，函数f(x)的极限是a，记作：f(x)=a或者当x→∞时，f(x)→a.3.常数函数f(x)=c.(x∈R)，有f(x)=c.注意：f(x)存在，表示f(x)和f(x)都存在，且两者相等.所以f(x)中的∞既有+∞，又有－∞的意义，而数列极限an中的∞仅有+∞的意义三、讲解范例：例1分别就自变量x趋向于+∞和－∞的情况,讨论下列函数的变化趋势.(1)y=()x分析：作出这个函数的图象，由图就能看出变化趋势.解：由图可知，当x→+∞时，y=()x无限趋近于0，即　()x=0；当x→－∞时，y=()x无限趋近于+∞.极限不存在．(2)y=2x解：由图可知，\n当x→+∞时.y=2x无限趋近于+∞，极限不存在．当x→－∞时，y=2x无限趋近于0，即2x=0.(3)解：由图可知，当x→+∞时，f(x)的值为1，即f(x)=1;当x→－∞时，f(x)的值为－1，即f(x)=－1．说明：当x→+∞时，f(x)不是无限趋近于某个常数a，而是f(x)的值等于常数a，那么函数f(x)当x→+∞时的极限也就是a.x→－∞时，情况也是如此.四、课堂练习：1．1.对于函数y=，填写下表并画出函数的图象，观察当x→∞时，函数y的变化趋势.答案：当x→∞时，y=无限趋近于0.即=0.2.写出下列函数极限的值.(1)；(2)10x；(3)；(4)\n答案：⑴0⑵0⑶0⑷03.判断下列函数的极限：（1）（2）（3）（4）答案：⑴0⑵0⑶0⑷4五、小结：当x分别趋向于+∞，－∞，∞时，函数f(x)的极限，以及常数函数的极限，注意f(x)中的∞和数列极限an中的∞的不同意义.以概念为依据，结合函数图象，学会求一些函数的极限六、课后作业：1.判断下列函数的极限：（1）（2）（3）（4）（5）（6）（7）（8）答案：⑴0⑵0⑶-1⑷0⑸0⑹0⑺0⑻5七、板书设计（略）八、课后记：