高中数学 函数课时复习教案6 3页

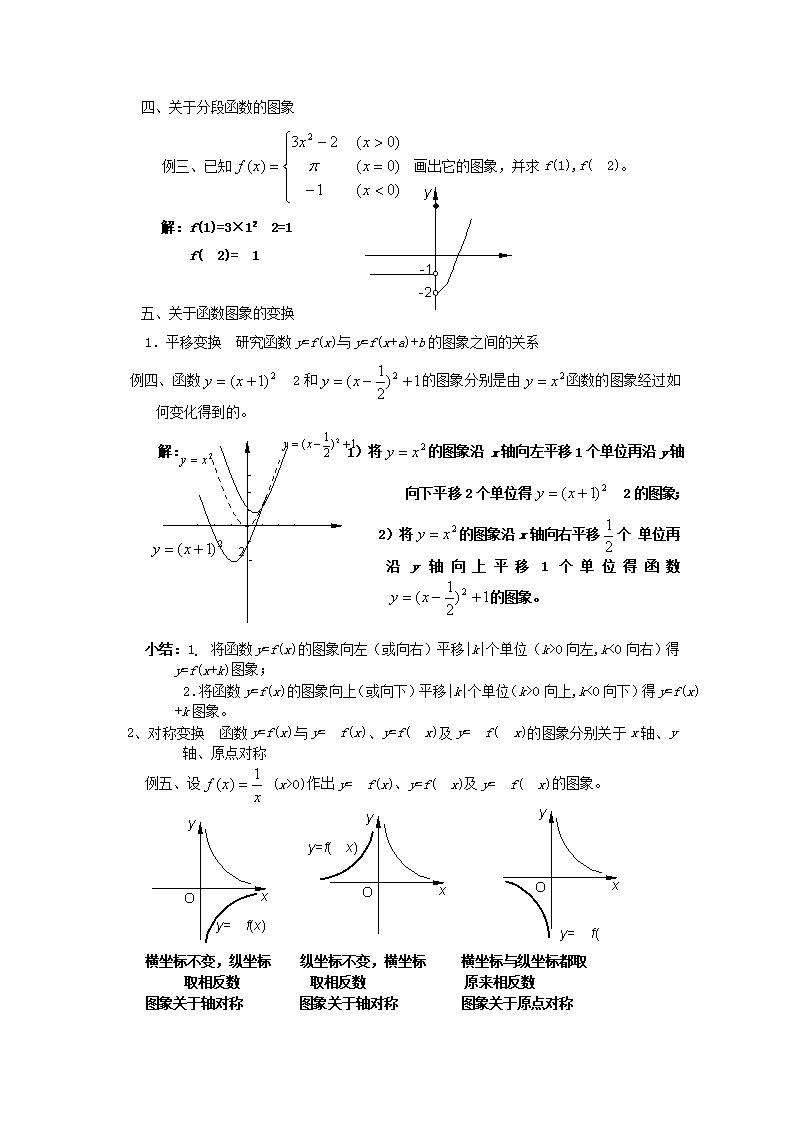
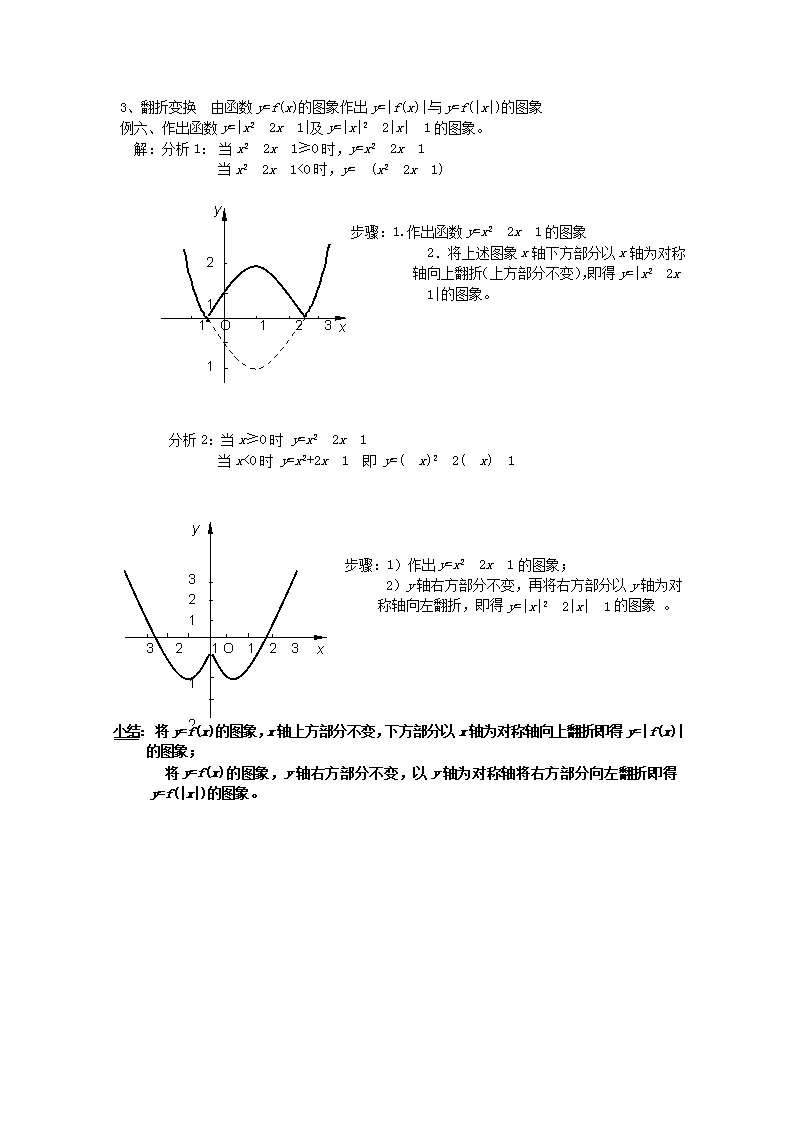
第六教时函数函数图象目的：要求学生根据函数解析式作出它们的图象，并且能根据图象分析函数的性质；同时了解图象的简单变换（平移变换和对称变换）。过程：一、复习：函数有哪三种表示方法？今天主要研究函数的图象。oxy123-111。2。解：解：oxy123-11注意：由于定义域从而导致函数图象只是若干个孤立点。-1-0.510.5yox3。注意：先写成分段函数再作图。解：定义域为且x¹强调：定义域十分重要。三、例二、根据所给定义域，画出函数的图象。-2-1O1234yx1234-2-1O1234yx1234-2-1O1234yx1234551。2。3。且xÎZ\n四、关于分段函数的图象-1-2py例三、已知画出它的图象，并求f(1),f(-2)。解：f(1)=3×12-2=1f(-2)=-1五、关于函数图象的变换1．平移变换研究函数y=f(x)与y=f(x+a)+b的图象之间的关系例四、函数-2和的图象分别是由函数的图象经过如何变化得到的。解：1）将的图象沿x轴向左平移1个单位再沿y轴向下平移2个单位得-2的图象；-22）将的图象沿x轴向右平移个单位再沿y轴向上平移1个单位得函数的图象。小结：1。将函数y=f(x)的图象向左（或向右）平移|k|个单位（k>0向左,k<0向右）得y=f(x+k)图象；2．将函数y=f(x)的图象向上（或向下）平移|k|个单位（k>0向上,k<0向下）得y=f(x)+k图象。2、对称变换函数y=f(x)与y=-f(x)、y=f(-x)及y=-f(-x)的图象分别关于x轴、y轴、原点对称yxOyxOyxOy=-f(x)y=f(-x)y=-f(-x)例五、设(x>0)作出y=-f(x)、y=f(-x)及y=-f(-x)的图象。横坐标不变，纵坐标纵坐标不变，横坐标横坐标与纵坐标都取取相反数取相反数原来相反数图象关于轴对称图象关于轴对称图象关于原点对称\n3、翻折变换由函数y=f(x)的图象作出y=|f(x)|与y=f(|x|)的图象例六、作出函数y=|x2-2x-1|及y=|x|2-2|x|-1的图象。解：分析1：当x2-2x-1≥0时，y=x2-2x-1当x2-2x-1<0时，y=-(x2-2x-1)yx-1O12321-1-2步骤：1.作出函数y=x2-2x-1的图象2．将上述图象x轴下方部分以x轴为对称轴向上翻折（上方部分不变），即得y=|x2-2x-1|的图象。分析2：当x≥0时y=x2-2x-1当x<0时y=x2+2x-1即y=(-x)2-2(-x)-1yx-3-2-1O123321-1-2-3步骤：1）作出y=x2-2x-1的图象；2）y轴右方部分不变，再将右方部分以y轴为对称轴向左翻折，即得y=|x|2-2|x|-1的图象。小结：将y=f(x)的图象，x轴上方部分不变，下方部分以x轴为对称轴向上翻折即得y=|f(x)|的图象；将y=f(x)的图象，y轴右方部分不变，以y轴为对称轴将右方部分向左翻折即得y=f(|x|)的图象。