高中数学 函数课时复习教案8 3页

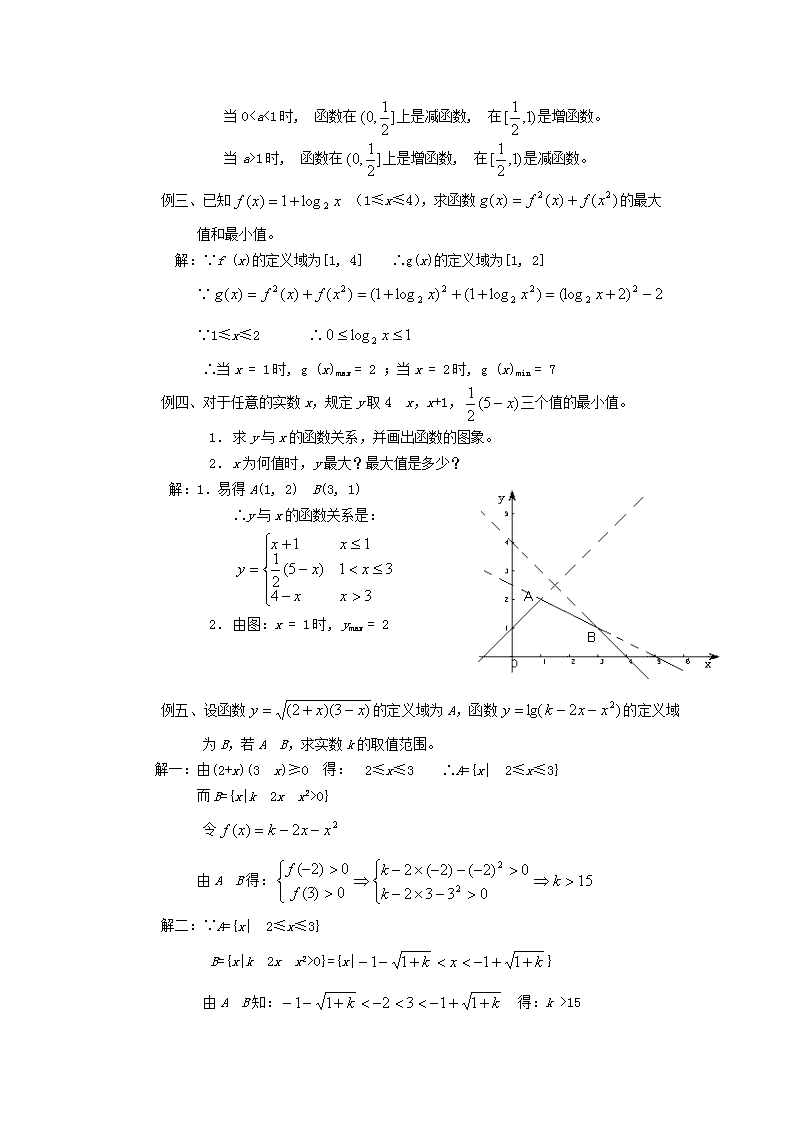
第八教时函数对数函数目的：重点复习对数及对数函数的有关内容，通过复习期望学生对知识有更深的理解过程：一、复习：对数概念，对数运算，换底公式，对数函数的概念、图象、性质二、例一、已知过原点O的一条直线与函数的图象交于A、B两点，过A作x轴的垂线，垂足为E，过点B作y轴的垂线，交EA于C，若C恰好在函数的图象上，试求A、B、C三点的坐标。CBAEF解：设A(x1,),B(x2,),则C(x1,)∵C在函数的图象上∴即：∴x2=x13又：即：∴∴由x1>1,∴log8x1¹1从而有：3x1=x13∴∴A、B、C三点的坐标分别为：例二、求函数(a>0,a¹1)的定义域、值域、单调区间。解：1．定义域：得：2．∵∴当01时,函数的值域为3．∵在区间内在上递增，在上递减。\n当01时,函数在上是增函数,在是减函数。例三、已知（1≤x≤4），求函数的最大值和最小值。解：∵f(x)的定义域为[1,4]∴g(x)的定义域为[1,2]∵∵1≤x≤2∴∴当x=1时,g(x)max=2；当x=2时,g(x)min=7例四、对于任意的实数x，规定y取4-x，x+1，三个值的最小值。1．求y与x的函数关系，并画出函数的图象。2．x为何值时，y最大？最大值是多少？解：1．易得A(1,2)B(3,1)∴y与x的函数关系是：AB2．由图：x=1时,ymax=2例五、设函数的定义域为A，函数的定义域为B，若AÍB，求实数k的取值范围。解一：由(2+x)(3-x)≥0得：-2≤x≤3∴A={x|-2≤x≤3}而B={x|k-2x-x2>0}令由AÍB得：解二：∵A={x|-2≤x≤3}B={x|k-2x-x2>0}={x|}由AÍB知：得：k>15\n例六、已知函数1°求f(x)的定义域、值域。2°判断并证明其单调性。解：1°∵a>1,由得：x<1∴f(x)的定义域为由知f(x)的值域为2°当时,由a>1知∴即∴f(x)为减函数。