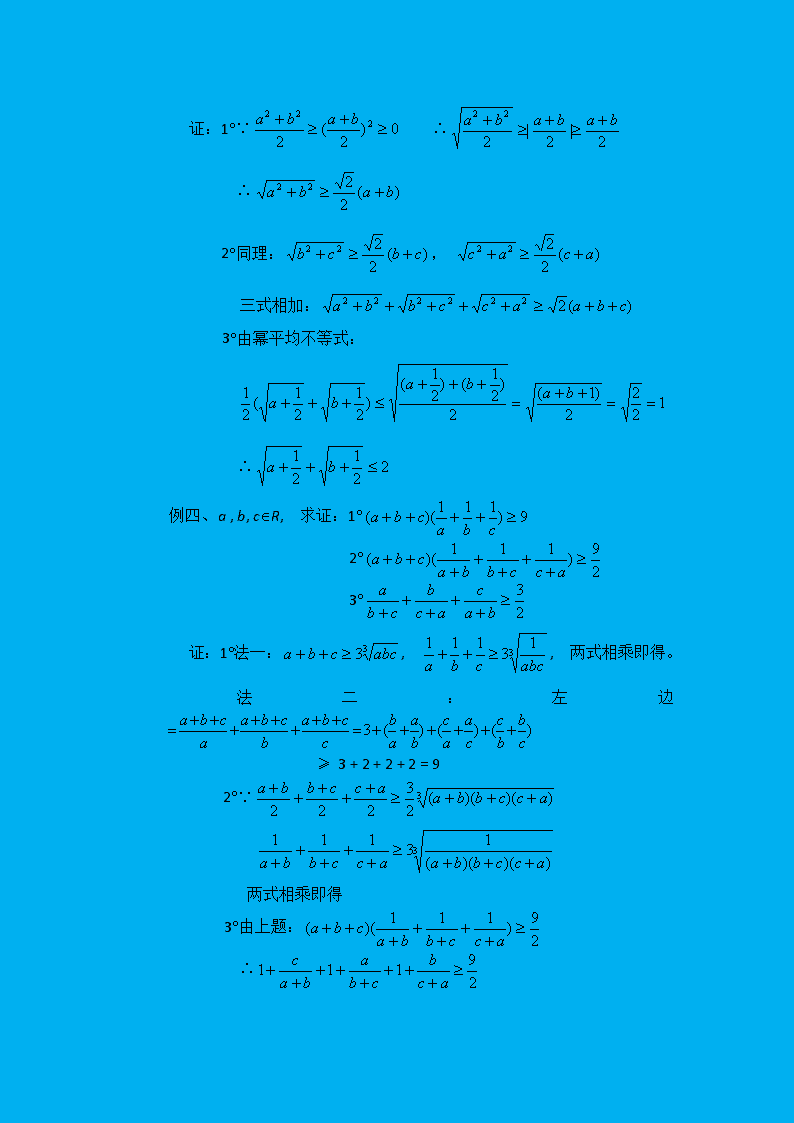- 191.56 KB
- 2022-08-17 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第七教时教材:不等式证明二(比较法、综合法)目的:加强比商法的训练,以期达到熟练技巧,同时要求学生初步掌握用综合法证明不等式。过程:一、比较法:1.复习:比较法,依据、步骤比商法,依据、步骤、适用题型2.例一、证明:在是增函数。证:设2≤x10,x1+x2-4>0∴又∵y1>0,∴y1>y2∴在是增函数二、综合法:定义:利用某些已经证明过的不等式和不等式的性质,推导出所要证明的不等式,这个证明方法叫综合法。例二、已知a,b,c是不全相等的正数,求证:a(b2+c2)+b(c2+a2)+c(a2+b2)>6abc证:∵b2+c2≥2bc,a>0,∴a(b2+c2)≥2abc同理:b(c2+a2)≥2abc,c(a2+b2)≥2abc∴a(b2+c2)+b(c2+a2)+c(a2+b2)≥6abc当且仅当b=c,c=a,a=b时取等号,而a,b,c是不全相等的正数∴a(b2+c2)+b(c2+a2)+c(a2+b2)>6abc例三、设a,b,cÎR,1°求证:2°求证:3°若a+b=1,求证:\n证:1°∵∴∴2°同理:,三式相加:3°由幂平均不等式:∴例二、a,b,cÎR,求证:1°2°3°证:1°法一:,,两式相乘即得。法二:左边≥3+2+2+2=92°∵两式相乘即得3°由上题:∴\n即:三、小结:综合法四、作业:P15—16练习1,2P18习题6.31,2,3补充:1.已知a,bÎR+且a¹b,求证:(取差)2.设aÎR,x,yÎR,求证:(取商)\n1.已知a,bÎR+,求证:证:∵a,bÎR+∴∴∴∴∴∴2.设a>0,b>0,且a+b=1,求证:证:∵∴∴∴第八教时教材:不等式证明三(分析法)目的:要求学生学会用分析法证明不等式。过程:一、介绍“分析法”:从求证的不等式出发,分析使这个不等式成立的充分条件,把证明不等式转化为判定这些充分条件是否具备的问题。二、例一、求证:证:∵综合法:只需证明:∵21<25展开得:∴\n即:∴∴∴即:21<25(显然成立)∴∴∴例二、设x>0,y>0,证明不等式:证一:(分析法)所证不等式即:即:即:只需证:∵成立∴证二:(综合法)∵∵x>0,y>0,∴例三、已知:a+b+c=0,求证:ab+bc+ca≤0证一:(综合法)∵a+b+c=0∴(a+b+c)2=0展开得:∴ab+bc+ca≤0证二:(分析法)要证ab+bc+ca≤0∵a+b+c=0故只需证ab+bc+ca≤(a+b+c)2即证:即:(显然)∴原式成立证三:∵a+b+c=0∴-c=a+b∴ab+bc+ca=ab+(a+b)c=ab-(a+b)2=-a2-b2-ab\n=例四、(课本例)证明:通过水管放水,当流速相等时,如果水管截面(指横截面)的周长相等,那么截面的圆的水管比截面是正方形的水管流量大。证:设截面周长为l,则周长为l的圆的半径为,截面积为,周长为l的正方形边长为,截面积为问题只需证:>即证:>两边同乘,得:因此只需证:4>p(显然成立)∴>也可用比较法(取商)证,也不困难。一、作业:P18练习1—3及习题6.3余下部分补充作业:1.已知00故只需证:即证:∵1+cosq>0只需证:即只需证:即:(成立)2.已知a>b>0,q为锐角,求证:略证:只需证:\n即:(成立)1.设a,b,c是的△ABC三边,S是三角形的面积,求证:略证:正弦、余弦定理代入得:即证:即:即证:(成立)第九教时教材:不等式证明四(换元法)目的:增强学生“换元”思想,能较熟练地利用换元手段解决某些不等式证明问题。过程:一、提出课题:(换元法)二、三角换元:例一、求证:证一:(综合法)∵即:∴证二:(换元法)∵∴令x=cosq,qÎ[0,p]则∵∴例二、已知x>0,y>0,2x+y=1,求证:证一:即:证二:由x>0,y>0,2x+y=1,可设\n则例三:若,求证:证:设,则例四:若x>1,y>1,求证:证:设则例五:已知:a>1,b>0,a-b=1,求证:证:∵a>1,b>0,a-b=1∴不妨设则∵,∴00,则证:设则(当a=1时取“=”)∴即∴原式成立二、小结:还有诸如“均值换元”“设差换元”的方法,有兴趣的课后还可进一步学习。三、作业:1.若,求证:2.若|a|<1,|b|<1,则3.若|x|≤1,求证:4.若a>1,b>0,a-b=1,求证:5.求证:6.已知|a|≤1,|b|≤1,求证: