高中数学(四种命题)教案 苏教版选修1-1 教案 5页

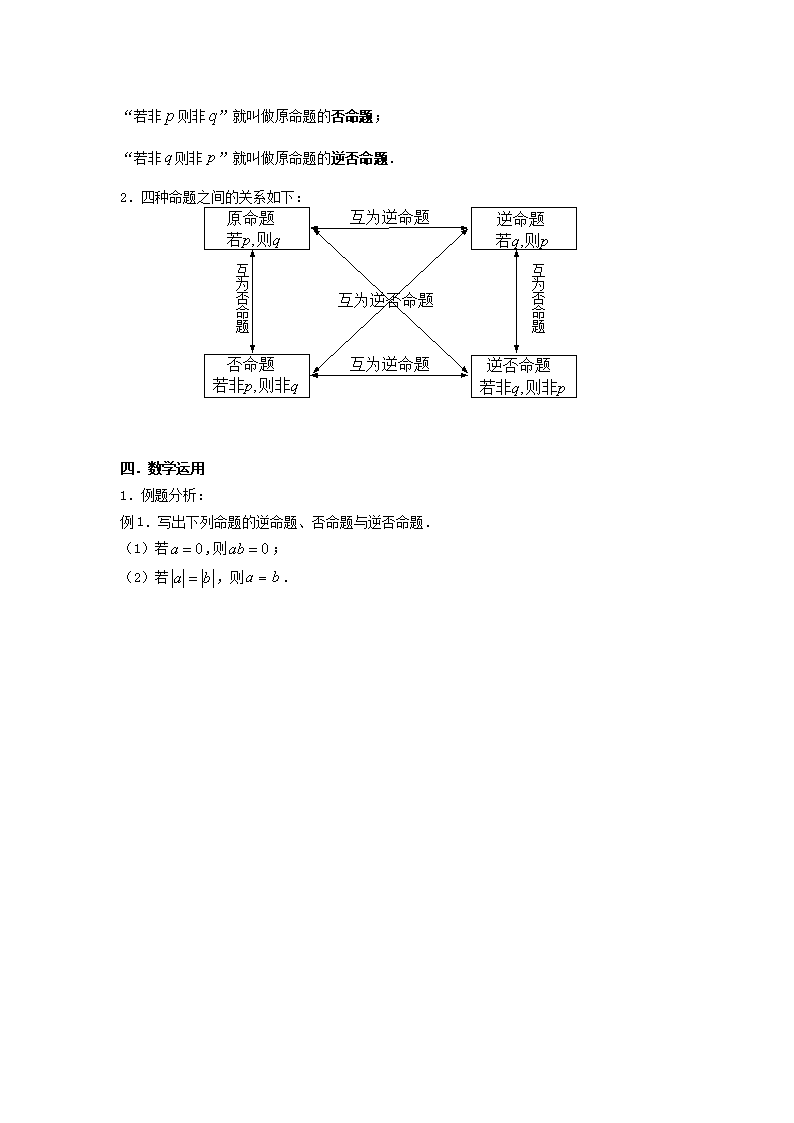
第一课时命题及其关系——四种命题教学目标:1．了解命题的逆命题、否命题和逆否命题的含义，能写出给定命题的逆命题、否命题和逆否命题；2．会分析四种命题之间的相互关系；3．会利用互为逆否命题的两个命题之间的关系判别命题的真假．教学重点：了解命题的逆命题、否命题和逆否命题的含义，能写出给定命题的逆命题、否命题和逆否命题．教学难点:会分析四种命题之间的相互关系.教学过程：一．问题情境1．情境我们知道，能够判断真假的语句叫做命题．例如，（1）如果两个三角形全等,那么它们的面积相等；（2）如果两个三角形的面积相等,那么它们全等；（3）如果两个三角形不全等,那么它们的面积不相等；（4）如果两个三角形的面积不相等,那么它们不全等.2．问题：命题（2）、（3）、（4）与命题（1）有何关系？二．学生活动1．上面的四个命题都是“如果……，那么……”形式的命题，可记为“若则”，其中是命题的条件，是命题的结论．2．在上面的例子中，命题（2）的条件和结论分别是命题（1）的结论和条件，我们称这两个命题为互逆命题．命题（3）的条件和结论分别是命题（1）的条件的否定和结论的否定，这两个命题称为互否命题．命题（4）的条件和结论分别是命题（1）的结论的否定和条件的否定，这两个命题称为互为逆否命题．三．建构数学1．一般地，设“若则”为原命题，那么“若则”就叫做原命题的逆命题；\n“若非则非”就叫做原命题的否命题；“若非则非”就叫做原命题的逆否命题．2．四种命题之间的关系如下：互为否命题互为否命题　四．数学运用1．例题分析：例1．写出下列命题的逆命题、否命题与逆否命题．（1）若,则；（2）若，则．\n思考：原命题、逆命题、否命题、逆否命题的真假有什么关系？例2．把下列命题改写成“若则”的形式，并写出它们的逆命题、否命题与逆否命题，同时指出它们的真假．（1）对顶角相等；（2）四条边相等的四边形是正方形．2．练习：（1）下列语句中是命题有．（填上所有符合题意的序号）①空集是任何集合的真子集；②把门关上；\n③垂直于同一直线的两条直线平行；④自然数是偶数吗？（2）下列命题：①若，则方程有实根；②函数是奇函数；③已知为全集，若，则；④若直线和平行，则．其中，真命题有．（填上所有符合题意的序号）（3）若命题的逆命题是，命题的逆否命题是，则是的．（填逆命题、否命题或逆否命题）（4）一个命题与它的逆命题，否命题，逆否命题这四个命题中()A真命题的个数一定是奇数B真命题的个数一定是偶数C真命题的个数可能是奇数,也可能是偶数D上述判断都不正确（5）对于命题“若数列是等比数列，则”，下列说法正确的是．（填上所有正确结论的序号）①它的逆命题是真命题；②它的否命题是真命题；③它的逆否命题是假命题；④它的否命题是假命题．五．回顾反思1．写一个命题的逆命题，否命题，逆否命题的关键是分清楚原命题的条件和结论(大前提不变)；2．在命题真假性的判断中，学会用互为逆否命题同真假的性质，通过“正难则反”培养自己的逆向思维能力．六．课后作业1．给出下列命题：①若，则；②若，则；③对于实数，若，则；④若，则；\n⑤正方形不是菱形．其中真命题是；假命题是．（填上所有符合题意的序号）2．将下列命题改写成“若则”的形式：（1）垂直于同一直线的两条直线平行；（2）斜率相等的两条直线平行；（3）钝角的余弦值是负数．3．写出下列各命题的逆命题、否命题和逆否命题并判断真假：（1）若两个事件是对立事件,则它们是互斥事件；（2）当时，若，则．