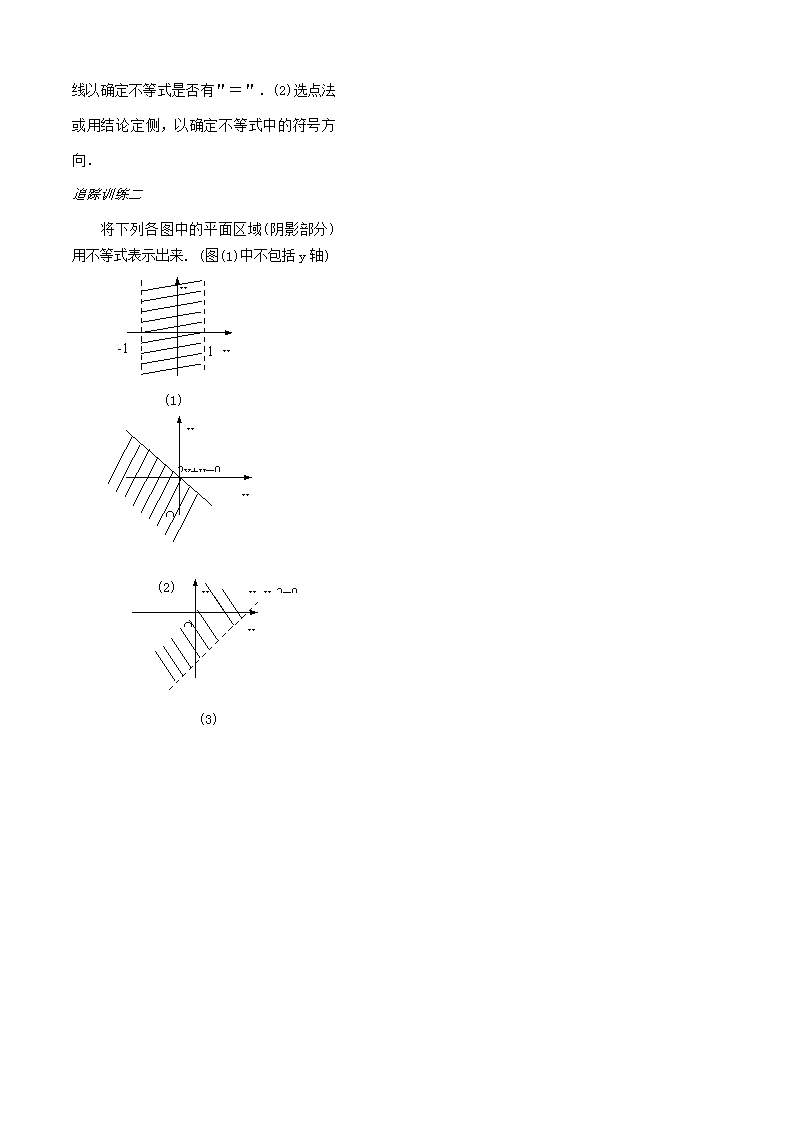高中数学(不等式)(学生版)教案4 苏教版必修5 教案 3页

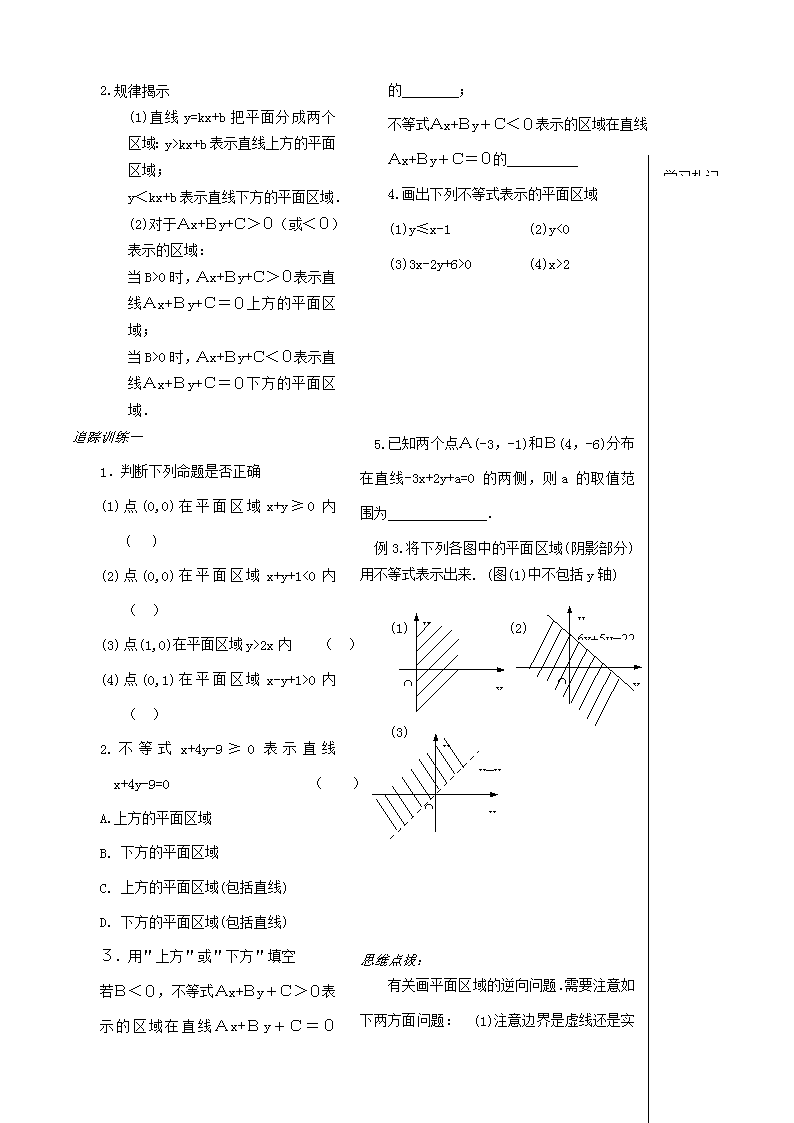
学习札记3.3二元一次不等式组与简单的线性规划问题第1课时【学习导航】知识网络作平面区域步骤含义二元一次不等式表示的平面区域逆向问题定侧方法学习要求1．了解二元一次不等式的几何意义，会作出二元一次不等式表示的平面区域．2．由二元一次不等式表示的平面区域能写出对应的不等式3．进一步体会数形结合的思想方法，开拓数学视野．【课堂互动】自学评价１．二元一次方程表示的图形是　　　　２．二元一次不等式表示平面区域的含义：　　　　　　　　　　。3.不等式x+y-1>0表示的平面区域：　　　　。【精典范例】例1．画出下列不等式所表示的平面区域(1)y>－2x+1(2)x－y+2>0(3)y≤－2x+3【解】例2.已知P(x0,y0)与点A(1,2)在直线l:3x+2y－8=0两侧,则()A.3x0+2y0>0B.3x0+2y0<0C.3x0+2y0>8D.3x0+2y0<8思维点拔：1.画平面区域的步骤：(1)先画不等式对应的方程所表示的直线（包括直线时，把直线画成实线，不包括直线时，把直线画成虚线）简称＂画线＂．(2)再通过选点法判定在直线的哪一侧．选点法中所选点常常为(0,0),(1,0)或(0,1)等，简称＂定侧＂\n2.规律揭示(1)直线y=kx+b把平面分成两个区域：y>kx+b表示直线上方的平面区域；y＜kx+b表示直线下方的平面区域．(2)对于Ａx+Ｂy+Ｃ＞０（或＜０）表示的区域：当B>0时，Ａx+Ｂy+Ｃ＞０表示直线Ａx+Ｂy+Ｃ＝０上方的平面区域；当B>0时，Ａx+Ｂy+Ｃ＜０表示直线Ａx+Ｂy+Ｃ＝０下方的平面区域．追踪训练一1．判断下列命题是否正确(1)点(0,0)在平面区域x+y≥0内　(　)(2)点(0,0)在平面区域x+y+1<0内（　）(3)点(1,0)在平面区域y>2x内（　）(4)点(0,1)在平面区域x-y+1>0内　（　）2.不等式x+4y-9≥0表示直线x+4y-9=0　　　　　　　（　　）A.上方的平面区域　B.下方的平面区域C.上方的平面区域(包括直线)D.下方的平面区域(包括直线)３．用＂上方＂或＂下方＂填空若Ｂ＜０，不等式Ａx+Ｂy＋Ｃ＞０表示的区域在直线Ａx+Ｂy＋Ｃ＝０的　　　　；不等式Ａx+Ｂy＋Ｃ＜０表示的区域在直线Ａx+Ｂy＋Ｃ＝０的　　　　　4.画出下列不等式表示的平面区域(1)y≤x-1　　　　　(2)y<0(3)3x-2y+6>0　　　　(4)x>25.已知两个点Ａ(-3，-1)和Ｂ(4，-6)分布在直线-3x+2y+a=0的两侧，则a的取值范围为　　　　　．例3.将下列各图中的平面区域(阴影部分)用不等式表示出来.(图(1)中不包括y轴)yxO6x+5y=22y(1)(2)OxyxOy=x(3)学习札记【师生互动】学生质疑教师释疑思维点拔：\n有关画平面区域的逆向问题．需要注意如下两方面问题：　(1)注意边界是虚线还是实线以确定不等式是否有＂＝＂．(2)选点法或用结论定侧，以确定不等式中的符号方向．追踪训练二将下列各图中的平面区域(阴影部分)用不等式表示出来.(图(1)中不包括y轴)x-1y1(1)yx2x+y=0Oyx-y-2=0(2)Ox(3)