高中数学 12三视图教案 新人教A版必修2 教案 5页

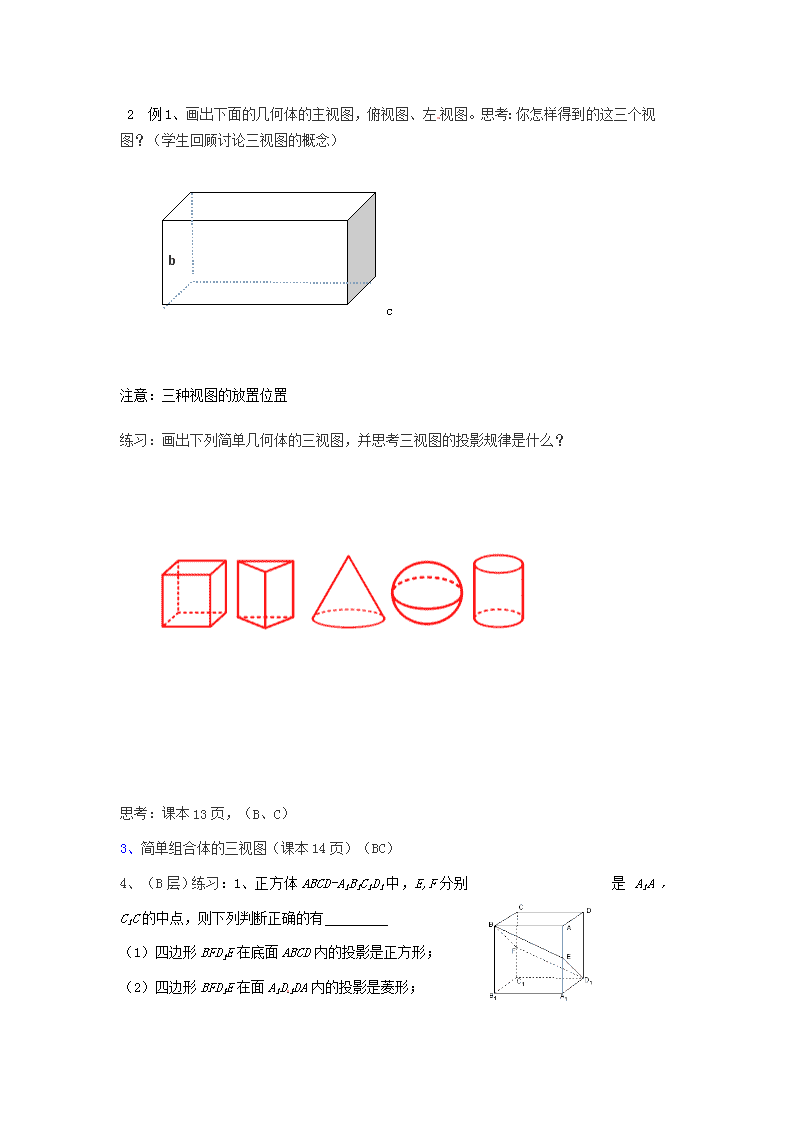
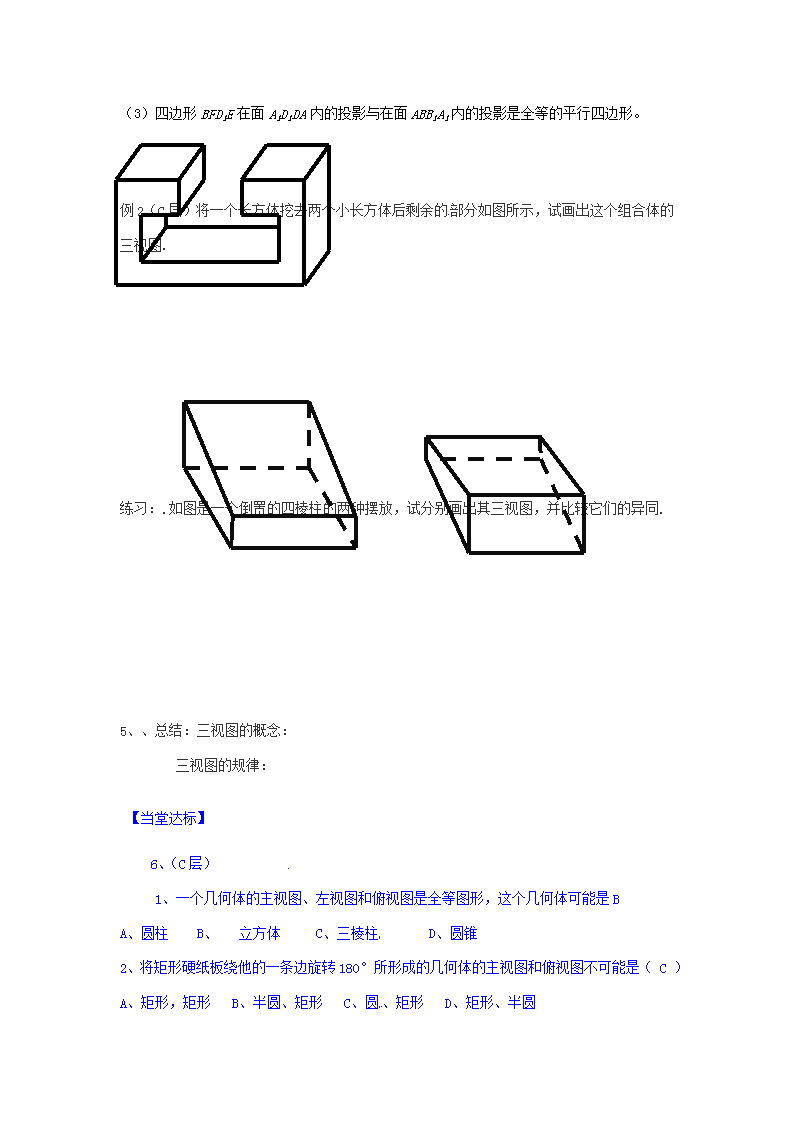
三视图（第一课时）教学目标：A、B层：掌握简单几何体的三视图C、层：使学生掌握组合体的三视图。教学重点、难点：会画简单几何体、组合体的三视图教学过程：一、复习、1、回想下列几何体的定义柱体：椎体：台体：2、预习、投影：投影线投影面、中心投影：、平行投影：、正投影：二、新授：1、概念：正视图：侧视图：俯视图：\n2例1、画出下面的几何体的主视图，俯视图、左视图。思考：你怎样得到的这三个视图？（学生回顾讨论三视图的概念）bacc注意：三种视图的放置位置练习：画出下列简单几何体的三视图，并思考三视图的投影规律是什么？思考：课本13页，（B、C）3、简单组合体的三视图（课本14页）（BC）4、（B层）练习：1、正方体ABCD-A1B1C1D1中，E,F分别是A1A，C1C的中点，则下列判断正确的有（1）四边形BFD1E在底面ABCD内的投影是正方形；（2）四边形BFD1E在面A1D1DA内的投影是菱形；\n（3）四边形BFD1E在面A1D1DA内的投影与在面ABB1A1内的投影是全等的平行四边形。例2（C层）将一个长方体挖去两个小长方体后剩余的部分如图所示，试画出这个组合体的三视图.练习：.如图是一个倒置的四棱柱的两种摆放，试分别画出其三视图，并比较它们的异同.5、、总结：三视图的概念：三视图的规律：【当堂达标】6、（C层）1、一个几何体的主视图、左视图和俯视图是全等图形，这个几何体可能是BA、圆柱B、立方体C、三棱柱D、圆锥2、将矩形硬纸板绕他的一条边旋转180°所形成的几何体的主视图和俯视图不可能是（C）A、矩形，矩形B、半圆、矩形C、圆、矩形D、矩形、半圆\n3、如图，E、F分别是正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的正投影可能是（要求把可能的图的序号都填上）。4、如果一个空间几何体的正视图和侧视图均为全等的等边三角形，俯视图为一个圆及其圆心，那么这个几何体为（）A.棱锥B.棱柱C.圆锥D.圆柱作业本：课本：15页，1题（AB层）2、（C）画出列几何体的三视图\n