2021年【教案】高中数学教案集合与常用逻辑用语 32页

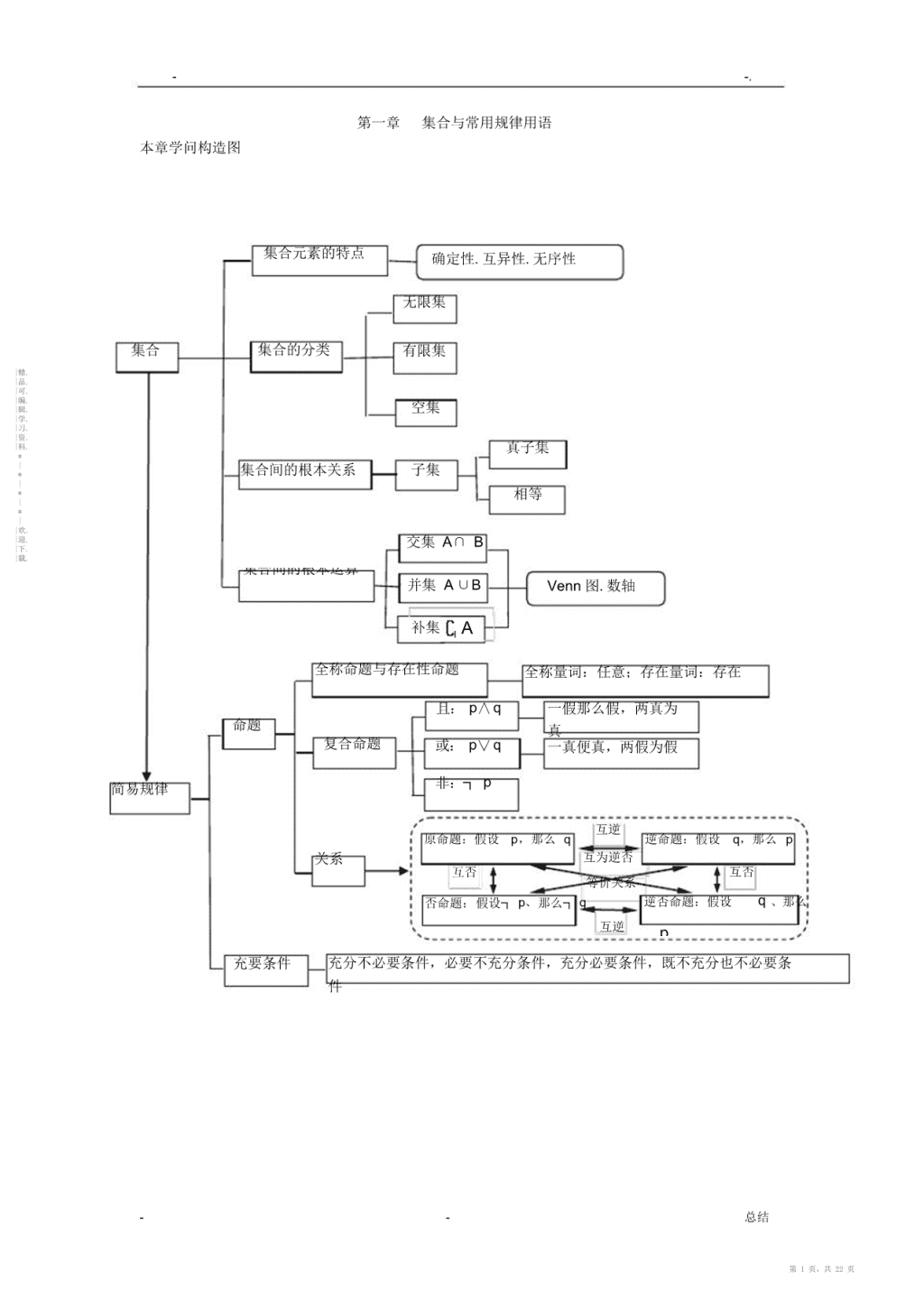
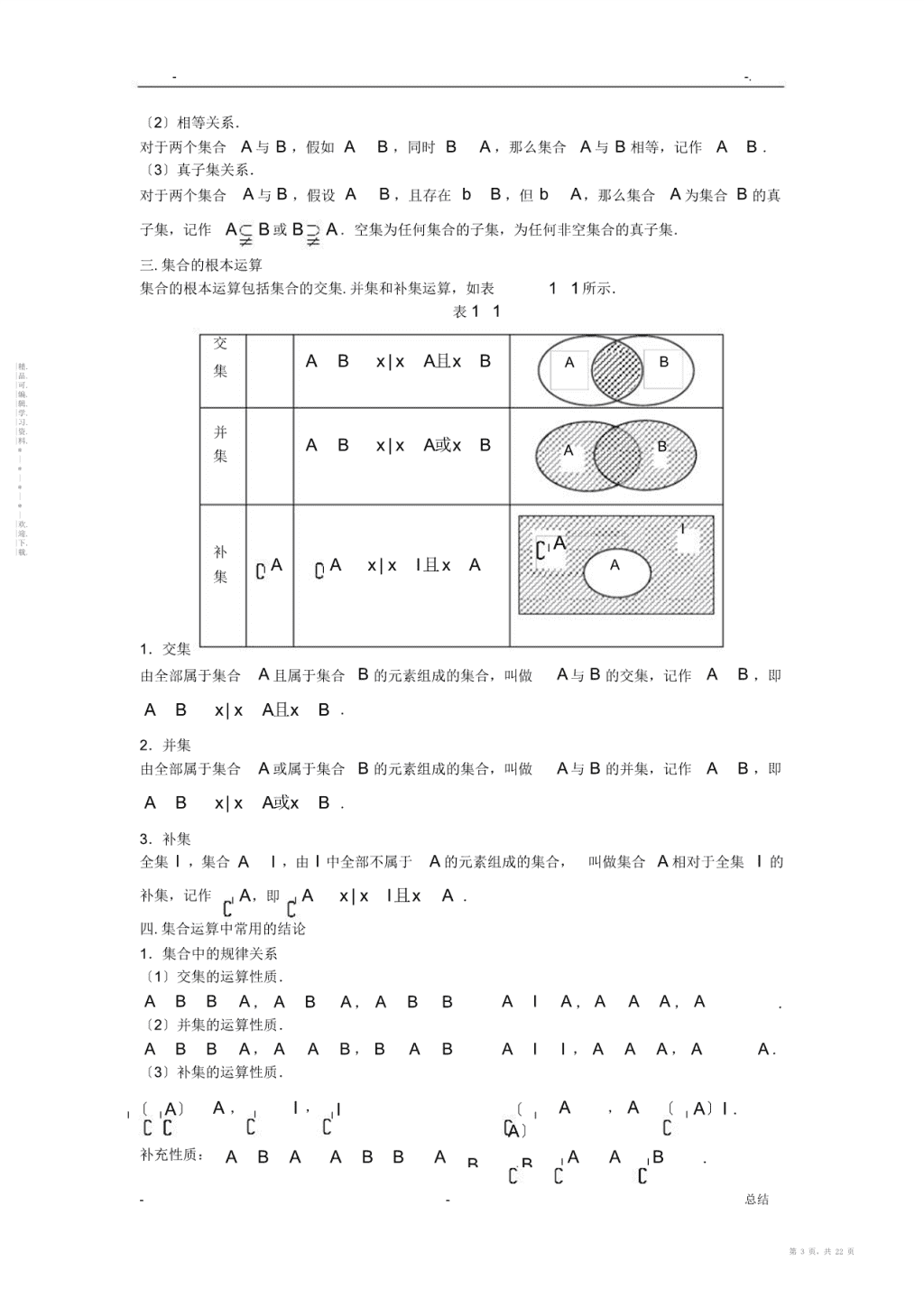
--.第一章集合与常用规律用语本章学问构造图集合元素的特点确定性.互异性.无序性无限集集合集合的分类有限集|精.|品.|可.|编.|辑.空集|学.|习.|资.|料.真子集*|*集合间的根本关系子集|*相等|*||欢.|迎.交集A∩B|下.|载.集合间的根本运算并集A∪BVenn图.数轴补集AI全称命题与存在性命题全称量词：任意；存在量词：存在且：p∧q一假那么假，两真为命题真复合命题或：p∨q一真便真，两假为假非：┐p简易规律互逆原命题：假设p，那么q逆命题：假设q，那么p关系互为逆否互否互否等价关系否命题：假设┐p、那么┐q逆否命题：假设q、那么互逆p充要条件充分不必要条件，必要不充分条件，充分必要条件，既不充分也不必要条件--总结第1页，共22页\n--.第一节集合考纲解读1.集合的含义与表示．明白集合的含义.元素与集合的关系；能用自然语言.图形语言和集合语言〔列举法或描述法〕描述不同的详细问题．2.集合间的根本关系．懂得集合之间包含与相等的含义．能识别给定集合的子集；在详细的情境中，明白全集与空集的含义．3.集合的根本运算．懂得两个集合的并集与交集的含义，会求两个简洁集合的并集与交集；懂得在给定集合中一个子集的含义，会求给定子集的补集；能使用韦恩〔Venn〕图表达集合的关系及运算．命题趋势探究有关集合的高考试题，考察重点为集合与集合之间的关系与运算，考试形式多以一道挑选题|精.|品.为主，分值5分．近年来试题加强了对集合运算和化简才能的考察，并向无限集方向开展，|可.|编.|辑.考察同学的抽象思维才能，在解决这些问题时，要留意运用数轴法和特别值法解题，应加强|学.|习.|资.集合表示方法的转化和化简的训练．|料.*猜测2021年以后的高考，将连续表达本章学问的工具性作用，多以小题形式显现，也有可|*|能会将其渗透在解答题的表达之中，相对独立．详细估量为：*|〔1〕以挑选题或填空题形式显现．.重庆等地也可能以集合为根底，综合其他学问在最终一*||欢.题的位置显现．考察同学的综合推理才能．|迎.|下.|载.〔2〕热点为集合间的根本运算.数轴法的应用和表达集合的语言工具作用．学问点精讲一.集合的有关概念1．集合的含义与表示某些指定对象的局部或全体构成一个集合．构成集合的元素除了常见的数.点等数学对象外，仍可以为其他对象．2．集合元素的特点〔1〕确定性：集合中的元素必需为确定的，任何一个对象都能明确判定出它为否为该集合中的元素．〔2〕互异性：集合中任何两个元素都为互不一样的，即一样元素在同一个集合中不能重复显现．〔3〕无序性：集合与其组成元素的次序无关．如a、b、ca、c、b．3．集合的常用表示法集合的常用表示法有列举法.描述法.图示法〔韦恩图.数轴〕和区间法．4．常用数集的表示*R一实数集Q一有理数集Z一整数集N一自然数集N或N一正整数集C一复数集二.集合间的关系1．元素与集合之间的关系元素与集合之间的关系包括属于〔记作aA〕和不属于〔记作aA〕两种．空集：不含有任何元素的集合，记作．2．集合与集合之间的关系〔1〕包含关系．子集：假如对任意aAAB，那么集合A为集合B的子集，记为AB或BA，明显AA．规定：A．--总结第2页，共22页\n--.〔2〕相等关系．对于两个集合A与B，假如AB，同时BA，那么集合A与B相等，记作AB．〔3〕真子集关系．对于两个集合A与B，假设AB，且存在bB，但bA，那么集合A为集合B的真子集，记作AB或BA．空集为任何集合的子集，为任何非空集合的真子集．三.集合的根本运算集合的根本运算包括集合的交集.并集和补集运算，如表11所示．表11交|精.ABx|xA且xBAB|品.集|可.|编.|辑.|学.|习.|资.并|料.ABx|xA或xB*AB|集*|*|*||欢.|迎.I|下.AI|载.补IAIAx|xI且xAA集1．交集由全部属于集合A且属于集合B的元素组成的集合，叫做A与B的交集，记作AB，即ABx|xA且xB．2．并集由全部属于集合A或属于集合B的元素组成的集合，叫做A与B的并集，记作AB，即ABx|xA或xB．3．补集全集I，集合AI，由I中全部不属于A的元素组成的集合，叫做集合A相对于全集I的补集，记作IA，即IAx|xI且xA．四.集合运算中常用的结论1．集合中的规律关系〔1〕交集的运算性质．ABBA，ABA，ABBAIA，AAA，A．〔2〕并集的运算性质．ABBA，AAB，BABAII，AAA，AA．〔3〕补集的运算性质．I〔IA〕A，II，II〔IA，A〔IA〕I．A〕补充性质：ABAABBABBIAAIB．I--总结第3页，共22页\n--.〔4〕结合律与安排律．结合律：A〔BC〕〔AB〕CA〔BC〕〔AB〕C．安排律：A〔BC〕〔AB〕〔AA〔BC〕〔AB〕〔AC〕．C〕〔5〕反演律〔德摩根定律〕．II〔AB〕IA〕I〔AB〕IA〕IB〕．B〔〔〕〔〔即“交的补补的并〞，“并的补补的交〞．*2．由n〔nN〕个元素组成的集合A的子集个数|精.|品.|可.Annnn|编.|辑.的子集有2个，非空子集有21个，真子集有21个，非空真子集有22个．|学.|习.|资.3．容斥原理|料.*|*Card〔ACard〔A〕Card〔B〕Card〔AB〕．|*B|〕*题型归纳及思路提示||欢.题型1集合的根本概念|迎.|下.|载.思路提示：利用集合元素的特点：确定性.无序性.互异性．b例1.1设a、bR，集合1、a0、，那么ba〔〕b、a、baA．1B．1C．2D．2b解析：由题意知01、ab、a，又a0，故ab0，得1，那么集合a1、0、a0、1、b，可11、ba2，应选C；得a、b变式1〔2021新课标理1〕集合A1、2、3、〔x、y〕|xA、yA，那么B中所4、5、B含元素的个数为〔〕．A．3B．6C．8D．10变式2〔2021山东理2〕集合A0、1、2、Bxy|xA、yA中元素的个数为〔〕．A．1B．3C．5D．9变式3假设集合x、xy、lg〔xy〕0、|x|、y，那么x，y．题型2集合间的根本关系思路提示〔1〕判定两集合的关系常用两种方法：一为规律分析法，即先化筒集合，再从表达式中寻\n找两集合的关系；二为用列举法表示各集合，从元素中查找关系，这表达了合情推理的思维方法．〔2〕两集合间的关系求参数时，关键为将两集合间的关系转化为元素的关系，进而转化为参数满意的关系，解决这类问题常利用数轴和韦恩图帮助分析．一.集合关系中的判定问题--总结第4页，共22页\n--.例1.2假设Ax|x4n1、nZ、Bx|x4n3、nZ、Cx|x8n1、nZ，那么A，B，C之间的关系为〔〕．A．CBAB．ABCC．CABD．ABC解析：解法一：集合B中元素x4n341)1、nZ，故集合AB，而集合C中〔n元素x42n1、nZ，故CA．|精.|品.解法二：列举A、7、、7、3、、7、1、9、．因|可.|编.3、1、5、9、、1、5、9、，C|辑.B|学.|习.此CAB，应选C．|资.|料.*|评注：解法一为数学中“求同比异〞的思想，值得学习；解法二为列举法，易于入手，也为*|做挑选题的常用方法．*|*|k1k1|欢.变式1设集合Mx|x、kZ，Mx|x、kZ，那么|迎.|下.2442|载.A．MNB．MNC．MND．MN2例1.3设Ax|x8x150、Bx|ax10.1〔1〕假设a，试判定集合A与集合B的关系；5〔2〕假设BA，求实数a组成的集合C.1分析：〔1〕先求集合A，再由a求集合B，确定A与B的关系.5〔2〕解方程ax10，建立a的关系式求a，从而确定集合C.2解析：〔1〕由x8x150得x3或x5，所以A3、5.11假设a，得x10，即x5，所以B5，故BA.55〔2〕由于A3，又BA.、5①当B时，那么方程ax10无解，那么a0；111②当B时，那么a0，由ax10，得x，所以3或5，即a11或aaaa3511故集合C0，，.35评注：〔1〕讨论集合的子集问题时应第一想到空集，由于空集为任何集合的子集.〔2〕含参数的一元一次方程axb解的确定：\n--总结第5页，共22页\n--.b当a0时，方程有唯独实数解x；a当ab0时，方程有很多多个解，可为为任意实数；当a0且b0时，方程无解.2变式1集合Ax|x3x100，集合Bx|p1x2p1，假设BA，求实数p的取值范畴.二.集合间的关系，求参数的取值范畴|精.|品.例1.4〔2021大纲全国理2〕集合A1、3、m、B1、m、ABA，那么m|可.|编.〔〕|辑.|学.|习.|资.|料.A．0或3B．0或3C．1或3D．1或3*|*|*解析：由ABA，得BA，故m3或mm且m1，所以m0或3.应选B.|*||欢.|迎.变式1集合Ax|3x6、Bx|xa、aR，假设AB，那么实数a的取值|下.|载.范畴为.变式2集合Ax|x1、Bx|xa，且ABR，那么实数a的取值范围为.2变式3集合Px|x1、Ma，假设PMP，那么a的取值范畴为〔〕A．〔、1]B．[1、〕C．[1、1]D．〔、1][1、〕三.集合关系中的子集个数问题2例1.5集合Ax|x3x100、xZ，那么集合A的子集个数为.分析：此题应第一确定集合A中元素的个数，再求其子集的个数.2解析：集合Ax|x3x100、xZ2、1、0、，共8个元素，那么集1、2、3、4、58合A的子集的个数为2256.2例1.6集合Ax|x3x20、xR、Bx|0x5、xN，满足条件ACB的集合C的个数为〔〕A．1B．2C．3D．4解析：由A1、21、且ACB，得集合C为集合1、2与集合3、4的任、2、B3、4一子集的并集，即求集合3、4的4，应选D.2子集的个数为2*2变式1集合M满意1M10x、|xx、\nN，求集合M的个数.--总结第6页，共22页\n--.题型3集合的运算思路分析但凡遇到集合的运算〔并.交.补〕问题，应留意对集合元素属性的懂得，数轴和韦恩图为集合交.并.补运算的有力工具，数形结合为解集合运算问题的常用思想.一.集合元素属性的懂得22例1.7集合My|yx1、xR、Nx|y9x，那么MN〔〕A．x|1x3B．x|1x3C．x|1x3D．x|1x4分析：在进展集合运算之前，第一要识别集合，即认清集合中元素的属性，判定M.N为数集仍为点集，为数集要化简集合，为点集要解方程组.在此题中，集合M代表元素为因变|精.|品.|可.量，故为函数的值域〔数集〕；集合N的代表元素为自变量，故为函数的定义域〔数集〕.|编.|辑.|学.222|习.解析：My|yx1、xRy|y1，Nx|y9xx|9x0，|资.|料.*|*即Nx|3x3，所以MNx|1x3，应选C.|*|*评注：几量遇到集合的运算〔交.并.补〕问题，应留意对集合元素属性的识别，如集合||欢.|迎.|下.y|yf〔x〕、xA为函数的值域，为数集，求出值域可以使之简化；集合|载.〔x、y〕|yf〔x〕、xA为点集，表示函数yf〔x〕图像上全部点的集合.再如集合22Mx|xy1、x、yR，可以理解为单位圆上点的纵坐标的取值集合y|1y1，表示的为数集[1、1]；〔x、y〕|0、yR表示的为曲线2Nxyx、22xy0，即抛的线yx上全部点构成的集合，它表示的为点集，故有MN.2另如M〔x、y〕|x4、Ny|yx，那么有MN，而易错为2yMN〔2、2〕、〔2、2〕.2变式1集合PxZ|0x3、MxR|x9，那么PM〔〕.A．1、2B．0、1、2C．x|0x3D．x|0x31变式2集合AxR||x3||x4|9、ByR|y4x6、0，那么集xx合AB.变式3设全集I〔x、y〕|x、yR，集合y3M〔x、y〕|1、〔x、y〕|，那么IM〕IN〕〔〕Nyx〔〔x2\n--总结第7页，共22页\n--.A．B．〔2、3〕D．〔x、y〕x1C．〔2、3〕|y2变式4集合A〔x、y〕|xmxy0、R，B〔x、y〕|x10、x，2xy0假设AB，求实数m的取值范畴.二.数轴在集合运算中的应用|精.|品.例1.8设集合Sx||x2|3、Tx|axa8、STR，那么a的取值范畴为|可.|编.|辑.〔〕|学.|习.|资.|料.A．〔3、1〕B．[3、1]C．〔[1、〕D．〔*|〔1、〕*|*|分析：借助数轴表示集合S和集合T，依据集合的关系，求解参数的取值范畴.*||欢.|迎.解析：由于Sx1或x5、Tx|axa8，集合S，T在数轴上的表示如图|下.|载.a11-1所示.由于STR，所以，可得3a1.应选A.a85a15a8图1—1变式1〔2021天津理11〕集合AxR||x2|3，集合BxR|〔xm〕2〕0，且AB〔1、，那么m，n.〔xn〕变式2全集UR，集合Ax|2x3、Bx|x1或x4，那么集合A〔U〔〕.B〕A.x|2x4B.x|x3或x4C.x|2x1D.x|1x3x3变式3集合Mx|0、Nx|x3，那么集合x|x1〔〕.x1A．MNB．MNC．R〔MD．R〔MN〕N〕三.韦恩图在集合运算中的应用例1.9设U为全集，M，P为两个非空集合，定义M与P的差集MPx|xM且xP，那么M〔MP〕\n〔〕.--总结第8页，共22页\n--.A．PB．MPC．MPD．M分析：此题可利用题中所给定义MP表示从集合M中去掉属于集合P的元素解题.解析：①当MP时，根据题意利用韦恩图解题，如图1-2所示，M〔MP〕MP.②当MP时，M〔MMMMP.P〕|精.|品.|可.|编.|辑.|学.|习.|资.|料.*|*|*|*||欢.|迎.|下.|载.综上，M〔MMP.应选B.P〕评注：但凡遇到抽象的集合运算题尝试利用韦恩图求解.此题也可用举例法求解，比方M2、1、，依据定义得出所求集合为空集.应选B.4、P3、5变式1设全集UMN1、2、3、4、UN，那么N〔〕.5，M2、4A．1、2、3B．1、3、5C．1、4、5D．2、3、4变式2某班级共有30人，其中15人宠爱篮球，8人宠爱足球，两项都不宠爱的有8人，那么宠爱篮球但不宠爱足球的有人．例1.10如图1-3所示，I为全集，A、B、C为它的子集，那么阴影局部所表示的集合为〔〕\nA．〔ACB．ICC．〔AB〕ICBB〕〔A〕--总结第9页，共22页\n--.D．〔IBA〕C分析：此题考察对利用韦恩图表述集合关系的懂得.解析：图1-3中的阴影局部为A与C的公共局部，即AC中去掉属于B的那局部元素后IC剩余元素组成的集合，即〔AC〕IB〕，应选B.B〔〔〕A对于韦恩图表述的集合应做如下懂得：阴影局部涉及到谁就交谁，涉及不到谁就交其补集．如图1-4所示分别表示：〔a〕ABC；〔b〕ABIC；IA〕IB〕C或〔c〕〔〔I〔AB〕C.|精.|品.|可.|编.|辑.|学.|习.|资.|料.*|*|*|*||欢.|迎.|下.|载.变式1M、N为集合I的非空子集，且M、N不相等，假设〔I，那么MNNM〕〔〕A．MB．NC．ID．四.以集合为载体的创新题例1.11设A为整数集的一个非空子集，对于kA，假如k1A且k1A，那么称k为A的一个孤立元，给定S1、2、3、4、，由S的3个元素组成的全部集合中，不5、6、7、8含孤立元的集合共有个.解析：由孤立元的定义，假设t不为A的孤立元，t应满意t1A或t1A，即集合中元素连续，故满意S的3个元素构成的不含孤立元的集合分别为1、2、3.2、3、4.3、4、5.4、5、6.5、6、7和6、7、8，共6个.评注：由S的3元素组成的集合中，含有一个孤立元的集合有30个，含有3个孤立元的集合有20个.变式1设S为整数集Z的非空子集，假如a、bS，有abS，那么称S关于数的乘法为封闭的，假设T、V为Z的两个不相交的非空子集，TVZ，且a、b、cT，有\nabcT，x、y、zV，有xyzV，那么以下结论恒成立的为〔〕--总结第10页，共22页\n--.A.T、V中至少有一个关于乘法为封闭B.T、V中至多有一个关于乘法为封闭C.T、V中有且只有一个关于乘法为封闭D.T、V中每一个关于乘法为封闭变式2集合Aa1、a2、2)，其中aiZ1、2、3、，由A中的元素构成、ak〔k〔i、k〕两个相应的集合S〔a、b〕|aA、bA、abA，T〔a、b〕|aA、bA、abA，其中〔a、b〕为有序数对，集合S和T中的元素个数分别为m和n.假设对于任意的aA，总有aA，那么称集合A具有性质P.|精.|品.|可.|编.〔1〕检验集合0、1、2、3与1、2、3为否具有性质P，并对具有性质|辑.|学.|习.|资.P的集合，写出相应的集合S和T；|料.*k〔k1〕|*〔2〕对任何具有性质P的集合A，证明：n.|*2|**|N|欢.变式3〔2021江苏23〕变式3设集合Pn1、2、3、，记f〔n〕为同时满意以下|迎.|下.、n、n|载.条件的集合A的个数.①APn；②假设xA，那么2xA；③假设xPnA，那么2xPnA.〔1〕求f〔4〕；〔2〕求f〔n〕的解析式〔用n表示〕.最有效训练题1〔限时45分钟〕21．设集合Mx|xx60、Nx|1x3，那么MN等于〔〕A．[2、3]B．[1、2]C．[2、3〕D．[1、2〕222．假设Ax|y4x、By|yx1，那么AB〔〕A．〔1、〕B．[1、2]C．[0、〕D．〔0、〕3．设全集U1、2、3、4、.集合A2、4、5、71、，那么如图1-5所示5、6、7、8，B4、7、8的阴影局部表示的集合为〔〕A．3、6B．2、4、6C．2、6D．3、4、6\n--总结第11页，共22页\n--.UAB图1—54．全集IR，集合Mx||x|2、xR、Px|xa，并且MIP，那么a的取值范畴为〔〕|精.|品.|可.|编.A．2B．a|a2C．a|a2D．a|a2|辑.|学.|习.|资.|料.*5．设集合Ax||xa|1、xR、Bx|1x5、xR.假设AB，那么实数a|*|的取值范畴为〔〕*|*|A．a|0a6B．a|a2或a4C．a|a0或a6|欢.|迎.|下.|载.D．a|2a46．设全集U〔xxR、yR、〔x、y〕|2xy0、〔x、y〕|xyn0、AmBy〕|，那么PA〔UB〕的充要条件为〔〕〔2、3〕A．m1且n5B．m1且n5C．m1且n5D．m1且n57．设集合A1、3、Ba2、2、AB3，那么实数a.2a18．集合A满意条件：当pA时，总有A〔p0且p1〕.2A，那么集合Ap1中全部元素的积等于.9．集合A、B满Ax|2x7、Bx|n1x2m1，且B.假设足〔UA〕B，那么m的取值范畴为.210．集合Ax|x4mx2m60、xR.假设A〔、，那么实数m的取值0〕范畴为.2211．集合Mm|mxy、x、yZ，假设对任m1、m2M，求证：m1m2M.意的12．集合1、2、3、、2n〔n\n*子集S，假设存．在．不大于n的正整数数N〕，对于A中的一个m，使得对S中的任．意．一对元素s1、s2，都|s1s2|m，那么称S具有性质P.有--总结第12页，共22页\n--.*〔1〕当n10时，试判定集合BxA|x9和CxA|x3kN为1、k否具有性质P？请说明理由.〔2〕假设集合S具有性质P，那么集合T2n1x|xS为否肯定具有性质P？请说明理由.|精.|品.|可.|编.|辑.|学.|习.|资.|料.*|*|*|*||欢.|迎.|下.|载.--总结\n第13页，共22页\n--.参考答案第一章集合与常用规律用语例1.1变式1解析：利用集合的概念及其表示求解，留意元素的特性；因为所以即、B中所含元素的个数为10.应选|精.|品.|可.D|编.|辑.例1.1变式2|学.|习.|资.|料.解析：逐个列举可得，时，时，*|*|*|时，*||欢.|迎.依据集合中元素的互异性可知集合B中元素为-2、-1、5个，应选C|下.|载.0、1、2共、例1.1变式3解析：依题意得、故即，因此假设那么故因此x=y=1与题意不符；假设那么明显与题意不符、故，此时满意题意；例1.2变式1解析集合M中的元素，分子为奇数；集合N中的元素，分子为整数，那么MN，应选B.例1.3变式1解析由，得，假设那么〔1〕当B=，即时，解得〔2〕当B时，如图1-9所示，由，得，得综上所述，实数的取值范畴为--总结第14页，共22页\n--.Ox-2p+12p-15图1-9评注：由，勿忘B=〔空集为任何集合的子集〕例1.4变式1解析由、如图1-10所示得，故实数的取值范畴为|精.|品.|可.|编.|辑.|学.B|习.|资.A|料.*–4–3–2|–1O123456a*|*图1-10|*||欢.|迎.评注端点值的判定通常为初学者的难题，我们可用假设法帮忙判定，即假设参数取端点后，|下.|载.与吻合，假设成立；假设与不吻合，那么假设不成立；例1.4变式2解析如图1-11所示，A为，B为，要使，只需，故实数的取值范畴为ABa1图1-11例1.4变式3解析由，得，那么，应选C.例1.6变式1解析由知，集合M为集合的任一非空子集与8集合的并集，所以集合M的个数为2-1=255评注求有限集的子集个数问题，有以下结论：n结论1：含有n个元素的集合的子集个数为、真子集个数为2-1，非空子nn集个数为2-1，非空真子集个数为2-2〕结论2设，那么有，--总结第15页，共22页\n--.①满意的集合A的个数为②满意的集合A的个数为-1③满意的集合A的个数为-1④满意的集合A的个数为-2例1.7变式1分析此题考察集合的概念与运算；|精.解析先化简再求交集，由得，故|品.|可.|编.|辑.|学.|习.，应选B|资.|料.*|*评注：此题假设无视集合P中元素的属性，易误将集合P等同于集合|*|例1.7变式2*||欢.|迎.解析，利用零点分段法解肯定值不等式；|下.|载.当时，;当时、、恒成立；当时、、综上所述、又由于，由根本不等式得、当时取，所以，故例1.7变式3解析解法一：M表示直线y=x+1上除去点〔2、3〕的局部，表示点〔2、3〕和除去直线y=x+1的局部，表示直线y=x+1上的点集，所以表示的点集中仅有点〔2、3〕，即〔2、3〕；解法二：，应选B例1.7变式4分析此题的几何背景为：抛物线与线段有公共点，求实数的取值范畴；--总结第16页，共22页\n--.解析解法一：问题等价于方程组在[0、2]上有解，即在[0、2]上有解，令，那么由知，抛物线过点〔0、1〕、所以抛物线在[0、2]上与x轴有交点等价于①或②|精.|品.|可.|编.|辑.|学.|习.由①得，由②得|资.|料.*|*所以实数的取值范畴为|*|*||欢.解法二：同解法一，问题等价于方程在[0、2]上有解，故可以转化为函|迎.|下.|载.数值域问题；等价转化为，当时，方程不成立；当时，方程转化为；当时，函数，即当时原方程有解，由，即所求实数的取值范畴为.例1.8变式1解析先求出集合A，再依据集合的交集运算求解；由于，当时，不符合题意，所以，即，又，所以.例1.8变式2解析、应选D例1.8变式3解析解法一：、所、得以.解法二：.应选D--总结第17页，共22页\n--.例1.9变式1解析由可得集合N中不含元素2、4，由排除法可知选项B正确，应选B.例1.9变式2分析此题中的集合关系比拟抽象，可以考虑使用韦恩图求解；解析作出韦恩图，如图1-12所示，设所求为人，那么宠爱篮球又宠爱足球的有15-人，喜爱足球不宠爱篮球的有人，故有.U篮球足球|精.|品.|可.|编.|辑.|学.|习.|资.x|料.15-x*x-7|*|*|*|8|欢.|迎.|下.图1-12|载.例1.10变式1解析如图1-13所示，由于，所以，所以，应选AIMN图1-13例1.11变式1解析由于，故整数1肯定在T、V两个集合中的一个中，不妨设，那么，由于，那么，即，从而T对乘法封闭；另一方面，当时，T关于乘法封闭，V关于乘法不封闭，故D不对，当时，T、V明显关于乘法都为封闭的，故B、C不对，应选A例1.11变式2解析〔1〕由于，故集合不具有性质P，集合具有性质P，其相应的集合S和T为.〔2〕首先，由A中元素构成的有序数对共有个，因为，所以--总结第18页，共22页\n--.又因为时，，所以当时，，从而集合T中元素的个数最多为、即.例1.11变式3解析〔1〕当n=4时，，满意条件的集合A有；所以.〔2〕解法一：任取偶数，那么必有奇数，使得；假设，那么，即为偶数，为奇数；假设，那么|精.|品.|可.|编.|辑.，即为奇数，为偶数；所以，任意偶数|学.|习.|资.|料.*为否属于集合A，完全由奇数确定；|*|*|设集合为由集合中全部奇数组成的集合，那么等于集合的子集个数，即*||欢.|迎.|下.|载.；解法二：易得、当为奇数时，集合中满意条件的集合A有个、对于集合，考虑元素n，由于n为奇数，所以均可，故.即，叠乘得.当为偶数时，集合中满意条件的集合A有个；对于集合，考虑元素n，由于n为偶数，所以，即n为否属于集合A、完全由确定；而集合中，对于每一个满意条件的集合A，元素为否属于集合A均为确定的，故为奇数，所以综上，.评注：①数列的核心为递推，先从特别的几个数〔n=1、2、3，.〕入手，关键在于发觉与的关系，从而发觉一般规律，再赐予证明；②递推法为处理数列问题〔乃至高校学习运算机等方面〕的“杀手锏〞，请读者深思体会，--总结第19页，共22页\n--.并能敏捷运用；最有效训练题11.D解析因为，所以，应选D.2.B解析由于，所以，应选B|精.|品.3.A解析阴影局部所表示的集合为，而，故|可.|编.|辑.|学.|习.，应选A.|资.|料.*|*4.C解析由于，，如图1-14所示，|*|*|利用数轴可得.应选C.|欢.|迎.|下.|载.CIPM-2O2a图1-145.C解析由，即，如图1-15所示，xa-1a+115或x15a-1a+1图1-15由图可知，所以，应选C6.D解析由于，所以，又，所以.应选D7.-1解析，所以，此时，不--总结第20页，共22页\n--.满意集合元素的互异性，故舍去.假设，同样舍去，当时，，满意题意，所以.8.1解析依题意，所以、从而故A中只有三个元素，|精.|品.它们的积为.|可.|编.|辑.|学.|习.9.解析由，得，那么|资.|料.*|*，解得，所以的取值范畴为.|*|*|10.解析解法一〔直接法〕即原方程有一个负根或两个负根，所以|欢.|迎.|下.|载.、解得、那么实数的取值范畴为解法二：〔间接法〕设全集}、设方程的两根为假设方程的根式均非负，那么、解得.由于，所以关于的补集即为所求.11.解析设、由于.所以、故.证毕12.解析〔1〕当时，集合，集合--总结第21页，共22页\n--.不具有性质P，由于对任意不大于10的正整数，都可以找到集合B中两元素，使得成立；集合具有性质P，由于可取，对于该集合中任意一对元素、都有〔2〕假设集合S具有性质P、那么集合肯定具有性质P.|精.|品.|可.|编.第一由于，任取，其中，由于，所以|辑.|学.|习.|资.|料.，从而，即，所以；由S具有性质P，可*|*|*知存在不大于n的正整数，使得对S中的任意一对元素，都有，对上述|*||欢.|迎.取定的不大于n的正整数，从集合中任取元素|下.|载.，其中，都有，由于，所以有，即，所以集合具有性质P--总结第22页，共22页