高中数学函数的图象2 教案 6页

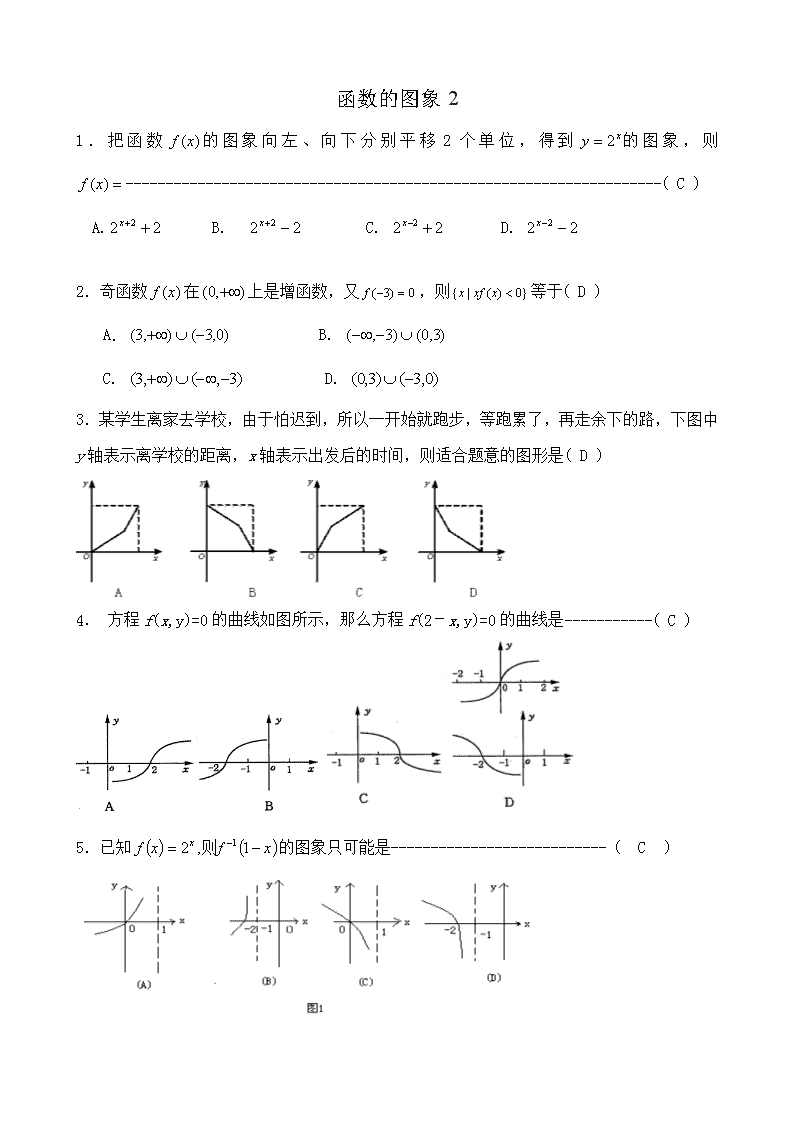
函数的图象21．把函数的图象向左、向下分别平移2个单位，得到的图象，则-------------------------------------------------------------------(C)A.B.C.D.2．奇函数在上是增函数，又，则等于(D)A．B.C.D.3．某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了，再走余下的路，下图中y轴表示离学校的距离，x轴表示出发后的时间，则适合题意的图形是(D)4．方程f(x,y)=0的曲线如图所示，那么方程f(2－x,y)=0的曲线是-----------(C)5．已知的图象只可能是---------------------------（C）\n012x01x－10x01xyyyy6．函数f(x)＝10x－1,则的图像是------------------------------(A) A.B.C.D. 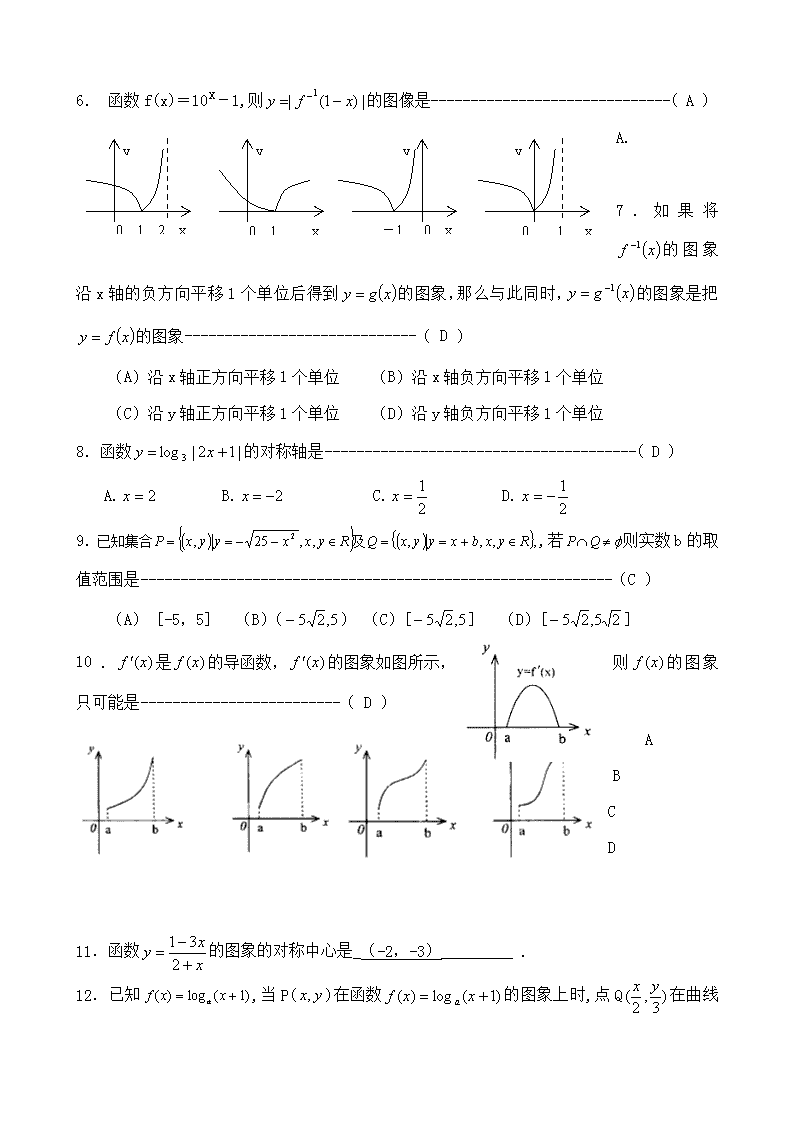7．如果将的图象沿x轴的负方向平移1个单位后得到的图象，那么与此同时，的图象是把的图象-----------------------------（D） 　　（A）沿x轴正方向平移1个单位　　（B）沿x轴负方向平移1个单位 　　（C）沿y轴正方向平移1个单位　　（D）沿y轴负方向平移1个单位8．函数的对称轴是---------------------------------------(D)A.B.C.D.9．,若则实数b的取值范围是-----------------------------------------------------------（C） 　　（A）[-5，5]（B）（）（C）[]（D）[]10．是的导函数，的图象如图所示，则的图象只可能是-------------------------（D）ABCD11．函数的图象的对称中心是_（-2，-3）_________.12．已知,当P()在函数的图象上时,点Q在曲线\n上,则的解析式是.13．设函数f(x)的图象关于点（1,2）对称，且存在反函数,f(4)＝0，则＝　-2.14．若方程有两个不同的实根,则的取值范围是.15．是定义在R上的偶函数，其图象关于直线对称，且当时，，则当时，=_-（x+4）2+1__.16．设函数的定义域为R，则下列命题中：①若为偶函数，则的图象关于轴对称；②若为偶函数，则的图象关于直线对称；③若，则的图象关于直线对称；④函数与函数的图象关于直线对称.则其中正确命题的序号是②、④17．设函数的图象为C1，C1关于点对称的图象为C2，C2对应的函数为.⑴求的解析表达式；⑵若直线y=b与C2只有一个交点，求b的值，并求出交点坐标；(3)解不等式.解：(1)g(x)=x－2+.(2)b=4时，交点为(5，4)；b=0时，交点为(3，0).(3)不等式的解集为{x|4＜x＜或x>6.18．为何值时，直线与曲线有两个公共点？有一个公共点？无公共点？\n解：作出的图象（如图半圆）与的图象（如图平行的直线，将代入得，将代入得，当与半圆相切于P时可求得则①当时，与曲线有两个公共点；②当或时，有一个公共点；③当或时，无公共点；19．已知函数f(x)是y=－1(x∈R)的反函数，函数g(x)的图象与函数y=－的图象关于y轴对称，设F(x)=f(x)+g(x).(1)求函数F(x)的解析式及定义域；(2)试问在函数F(x)的图象上是否存在两个不同的点A、B，使直线AB恰好与y轴垂直？若存在，求出A、B的坐标；若不存在，说明理由.解：(1)y=－1的反函数为f(x)=lg(－1＜x＜1.由已知得g(x)=,∴F(x)=lg+,定义域为(－1，1).(2)用定义可证明函数u==－1+是(－1，1）上的减函数，且y=lgu是增函数.∴f(x)是(－1，1）上的减函数，故不存在符合条件的点A、B.20．已知函数F(x)=|2x－t|－x3+x+1（x∈R，t为常数，t∈R）（1）写出此函数F(x)在R上的单调区间；（2）若方程F(x)－k=0恰有两解，求实数k的值。解：（1）∴由－3x2+3=0得x1=－1，x2=1，而－3x2－1<0恒成立\n∴①当<－1时，F(x)在区间(－∞，－1)上是减函数在区间(－1，1)上是增函数，在区间(1，+∞)上是减函数②当1>≥－1时，F(x)在区间(－∞，)上是减函数在区间(，1)上是增函数，在区间(1，+∞)上是减函数③当≥1时，F(x)在(－∞，+∞)上是减函数（2）由1）可知①当<－1时，F(x)在x=－1处取得极小值－1－t，在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，此时m=－1－t或m=3－t②当－1≤<1，F(x)在x=处取值为，在x=1处取得极大值3－t，若方程F(x)－m=0恰有两解，此时m=或m=3－t③当≥1时，不存在这样的实数m，使得F(x)－m=0恰有两解21．设函数（）的图象关于原点对称，且时，取极小值⑴求的值；⑵当时，图象上是否存在两点，使得过此两点处的切线互相垂直？试证明你的结论。解：①函数的图象关于原点对称对任意实数，有即恒成立时，取极小值，且②当时，图象上不存在这样的两点使结论成立。\n假设图象上存在两点，使得过此两点处的切线互相垂直，则由知两点处的切线斜率分别为且（*）[-1，1]与（*）矛盾。